Глава 5. Формула Тейлора и исследование функций. §5.1.Формула Тейлора.

Пусть функция имеет непрерывные производные до -го порядка включительно в некоторой окрестности точки . Возьмём произвольное значение из этой окрестности и зафиксируем его. Очевидно,

, т.е. . (1)

Последний интеграл вычислим по частям

Подставим в (1) и получим (2)

Последний интеграл снова вычислим по частям

и подставим в (2). Получим

Повторяя эту операцию раз, имеем

(3)

Формулу (3) называют формулой Тейлора для функции в окрестности точки . Эта формула верна во всей окрестности . Многочлен

(4)

называют многочленом Тейлора – го порядка для функции в точке , а его коэффициенты называют коэффициентами Тейлора.

Последнее слагаемое из формулы (3) (5)

называют остаточным членом формулы Тейлора в интегральной форме.

Получим две другие формы остаточного члена формулы Тейлора.

1º. Остаточный член в форме Лагранжа.

Если в (5) использовать обобщённую теорему о среднем значении для непрерывной функции , то ,  – между и . Таким образом, мы получили остаточный член формулы Тейлора в форме Лагранжа .

То же самое в иной форме (6)

2º. Остаточный член в форме Пеано.

Если и непрерывна, то . Отсюда следует, что .

Подставляя в (6), имеем .

Поскольку , то .

Таким образом, . Подставляя в (3), имеем (7)

– формула Тейлора с остаточным членом в форме Пеано.

Чем отличается формула (7) от (3)? (в (7) степень многочлена Тейлора на единицу больше, но остаточный член только качественный.В (3) он числовой.

Теорема (о единственности многочлена Тейлора). Пусть функция имеет непрерывные производные до порядка в окрестности точки и

. (8)

Тода (9)

□ Пользуясь формулой Тейлора с остаточным членом в форме Пеано (7), запишем равенство = . (10)

Переходя в (10) к пределу при , получим . Если отбросить в обеих частях в (10) одинаковые члены и и разделить затем обе части на , получим

Переходя в этом равенстве к пределу при , получим . Продолжая эти рассуждения, получим (9). ■

Замечание. Если каким то образом можно получить представление функции в виде (8), то согласно теореме это представление будет разложением функции по формуле Тейлора.

Пример. Из тождества (сумма геометрической прогрессии) имеем . А поскольку , то функция имеет следующее разложение по формул Тейлора .

Замечание. Формулу Тейлора, если , называют формулой Маклорена.

§5.2. Формула Тейлора для основных элементарных функций.

1º. Экспонента. Имеем . Откуда получаем (1)

2º. Гиперболические функции. Поскольку и

, (2)

то из (1) и (2) получим .

3º. Тригонометрические функции. Поскольку для имеем , то , а поэтому .

Аналогично для имеют место формулы , , а поэтому

4º. Логарифмическая функция. Для имеем

, а поэтому , откуда .

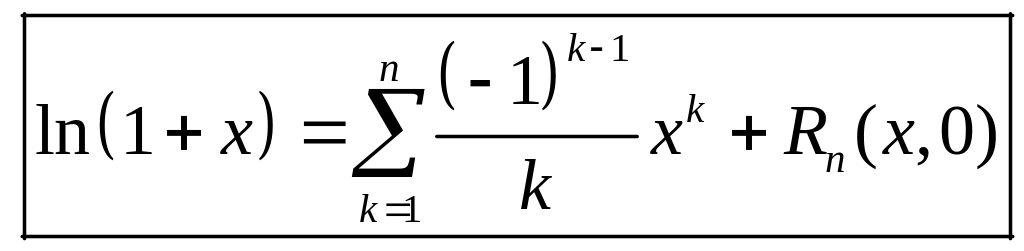5º. Степенной бином. Для имеем , а поэтому , , откуда

.

В частности .

Замечание. Если , то 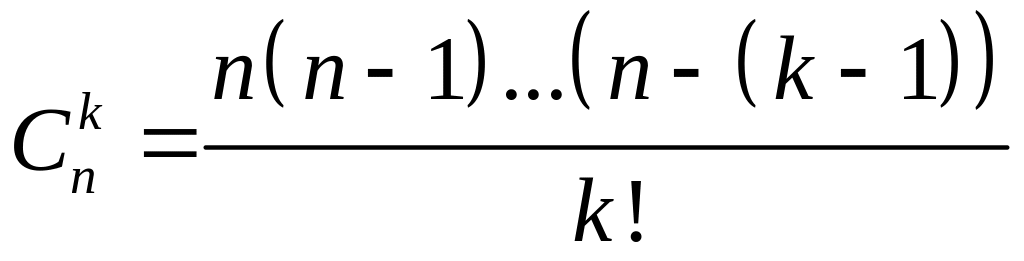, то и в формуле раразложения степенного бинома также используют обозначение , хотя .

Рассмотрим примеры использования формулы Тейлора.