Геометрическое изображение комплексного числа. Тригонометрическая форма комплексного числа.

Любое комплексное число можно изобразить на плоскости в прямоугольной системе координат.

z = a + bi

a

b

x

y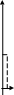

Если провести из начала координат прямую ОМ то говорят что задан вектор комплексного числа.

Тригонометрическая форма комплексного числа.

z = a + bi

b

y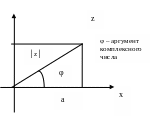

│z│ - модуль комплексного числа (или расстояние от начала координат до заданной точки)

│z│ =

b =│z│ * sin φ

, a=

z =│z│ cos φ + i│z│ sin φ

z =│z│ (cos φ + i sin φ) – тригонометрическая форма комплексного числа

№20

Действия над комплексными числами в тригонометрической форме.

Действия умножения, деления, возведения в степень и извлечение из корня значительно проще производить над комплексными числами, записанными в тригонометрической форме.

z₁ =│z₁│ (cos φ₁ + i sin φ₁)

z₂ = │z₂│ (cos φ₂ + i sin φ₂)

Умножение:

z₁ * z₂ =│z₁│ * │z₂│ (cos (φ₁ + φ₂) + i sin (φ₁ + φ₂))

(модули перемножают, а аргументы складывают).

Деление:

(cos (φ₁ - φ₂) + i sin (φ₁ - φ₂))

(первый модуль делят на второй, а из первого аргумента вычитают второй).

Возведение в степень (целую положительную):

Производят по формуле Муавра

(│z│(cos φ + i sin φ))ⁿ = │z│ⁿ (cos n φ + i sin n φ)

(модуль возводят в ту же степень, а аргумент умножают на показатель степени).

№21

Дифференциальные уравнения с разделяющимися переменными. Схема решения.

Уравнения, приводящиеся к виду f₁(х) * f₂(у) dx = φ₁ (х) * φ₂ (у) dy называются дифференциальными уравнениями с разделяющимися переменными.

Схема решения.

1. Разделить переменные

2. Найти интегралы левой и правой части

3. Найти общее решение уравнения

4. Если необходимо, найти частное решение уравнения.

Пример: Решить уравнение

х=0 ,у=2

Решение:

ydy = -2xdx

∫ ydy= -2 ∫ xdx

у² = -2х² + с - общее решение

2² = 0+ с с=4

у² = - 2х² + 4 – частное решение

№22

Линейные однородные дифференциальные уравнения 2 порядка с постоянными коэффициентами.

Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида y” + py’ + qy = 0 (*) , где p и q – постоянные числа.

Схема решения данного уравнения.

Составим характеристическое уравнение r² + pr + q = 0 , где r² → y’’

r → y’

1 → y

Это квадратное уравнение, находим дискриминант D = p² – 4q

Если D > 0 , находим два корня r₁ и r₂, тогда y = c₁e^{r1 x} + c₂e^{r2 x} – общее решение уравнения (*), где с₁ и с₂ – постоянные числа.

Если D = 0 , находим один корень уравнения r, тогда y = e ^{r x} (c₁ + c₂ x) – общее решение уравнения (*), где с₁ и с₂ – постоянные числа.

Если D < 0 , находим корни уравнения в области комплексных чисел r_1,2 = a ± bi ,

тогда y = e ^ax (c₁ cos bx + c₂ sin bx) – общее решение уравнения (*) , где с₁ и с₂ – постоянные числа.

№23

Линейные дифференциальные уравнения 1 порядка.

Уравнения вида у’ + py = q , где p и q – функции от х или постоянные величины, называется линейным дифференциальным уравнением первого порядка.

Схема решения данного уравнения.

Пусть у = uv у’ = ( uv)’ = u’v + v’u или

Новые переменные подставим в исходное уравнение , получим:

(*)

Пусть – это дифференциальное уравнение с разделяющимися переменными.

Решая данное уравнение, найдем V.

Сейчас возвращаемся к уравнению (*), получим . Решая это уравнение, находим U. Далее находим искомую функцию y, т.к. у=uv.

№24

Числовые ряды, их сходимость и расходимость.

Пусть задана последовательность чисел: а₁,а₂ ,… а_n,….

Выражение а₁+а₂ +… а_n+…= (1) называется числовым рядом.

а₁, а₂,…а_n – называются членами ряда.

а_n- общий член ряда.

Члены ряда могут быть как положительными, так и отрицательными.

Пример:

1) =

2) =

Сумма первых n-членов ряда называется n-ой частичной суммой, т. е. S_n=a₁+a₂+…+a_n

Если существует конечный предел lim S_n=S, то он

называется суммой ряда (1). В этом случае ряд (1) называется сходящимся.

Если же lim S_n - ,бесконечный или вообще не существует, то ряд (1)

n→ ∞

называется расходящимся.