Необходимый признак сходимости ряда.

∞

Опр. Если ряд ∑ а_n сходится, то lim a_n= 0.

n=1 n→ ∞

Достаточные признаки сходимости положительных рядов.

1.Первый признак сравнения.

Если даны ряды с неотрицательными членами

∞

∑ a_n = a₁+ a₂+ … a_n+ …

n=1

∞

∑ b_n = b₁+ b₂+ … a_n+ …

n=1

Причем, начиная с некоторого номера а_n≤ b_n, то

а) из сходимости второго ряда следует сходимость первого ряда;

б) из расходимости первого ряда следует расходимость второго ряда.

Во многих случаях в качестве рядов сравнения берут геометрический или обобщенный гармонический ряд.

2. Второй признак сравнения.

∞ ∞

Если существует предел lim (a_n/b_n )= L ; (0< L < ∞), то ряды ∑ а_n и ∑ b_n

n=1 n=1

одновременно сходятся или расходятся.

2.Признак Даламбера.

∞

Если для ряда ∑ а_n существует предел lim ( a_n+1 /a_n )= L, то

n=1 n→ ∞

а) при L<1 данный ряд сходится;

б) при L>1 расходится;

в) если L=1, то требуется дополнительное исследование.

2. Радикальный признак Коши.

∞

Если для ряда ∑ а_n существует предел lim = L, то

n=1 n→ ∞

а) при L<1, ряд сходится;

б) при L>1, ряд расходится;

в) при L=1 требуется дополнительное исследование.

Знакочередующиеся ряды.

∞

Опр.Ряд вида ∑(-1)^n-1 а_n = a₁- a₂+ …(-1)^n-1 a_n+ … ; где a_n >0,

n=1

называется знакочередующимся рядом.

Пример:

Признак сходимости знакочередующегося ряда (признак Лейбница).

∞

Если для ряда вида ∑ (-1)^n-1а_{n ,} где a_n >0

n=1

1. a_n> a_n+1 ,начиная с некоторого номера

2. lim a_n = 0 ,

n→ ∞

то данный ряд сходится.

Пример:

Lim = 0 ,

n→ ∞

Признак сходимости знакопеременного ряда.

Если ряд │a_n│ сходится, то сходится и знакопеременный ряд a_n.

Пример: ряд сходится, так как сходится

ряд, составленный из абсолютных членов ряда

№25

Степенные ряды.

Степенным рядом называется функциональный ряд вида

∞

∑ a_nxⁿ = a₀ + a₁x + a₂x² + a₃x³ + … ,где а₀, а₁,-постоянные коэффициенты

n=0

Пример степенного ряда

∞

∑ (x²ⁿ/n) = x²/1 + x⁴/2 + x⁶/3 + …

n=1

Многие функции f(x) можно разложить в степенные ряды по формуле

Маклорена:

Примеры разложения функций в ряд Маклорена:

℮^x = 1 + x/1! + x²/2! + x³/3!+ …+ xⁿ/n! + …

Sin x = x/1! – x³/3! + …+(-1)ⁿ x²ⁿ⁺¹/(2n+1)! + …

Cos x = 1 – x²/2! + x⁴/4! - …+(-1)ⁿ x²ⁿ/(2n)! + …

(n! –читается как n –факториал и вычисляется: n! =

№26

Функциональные ряды их разложение в ряд Маклорена.

Ряд вида u_n(x) = u₁(x) + u₂(x) +… , члены которого есть функции от x, имеющие общую область определения, называется функциональным рядом.

Множество значений x , при которых функциональный ряд сходится, называется областью сходимости этого ряда.

Область сходимости функционального ряда определяется с помощью признаков сходимости для числовых рядов.

Примеры функциональных рядов:

∞

∑ cos nx/n² = cos x/1 + cos 2x/4 +…+ cos nx/n² +…

n=1

∞

∑ nx = x + 2x + 3x +…

n=1

№27

Множества и отношения.

Множество – это совокупность каких - либо объектов, объединяемых в целое некоторым общим признаком.

Например, множество студентов, множество книг, множество чисел.

Множества обозначаются буквами А, В, С.

Объекты, входящие в данное множество, называются элементами данного множества.

Например: 1) N={1,2,3…} – множество натуральных чисел.

2) A={Англия, Франция…} – множество стран Европы.

Элементы множества обозначаются буквами а, в, с…

Если элемент "а" принадлежит множеству "А", то записывают а А.

Способы задания множеств.

1. Перечисление: А={1,3,5,7…} В={в₁, в₂, в₃, в₄…}.

2. Указание характеристического свойства: А={x/P(x)} – множество А состоит из элементов "х", удовлетворяющих свойству Р(х).

Например: Если множество А состоит из точек интервала , то можно записать:

С помощью характеристических свойств записывают те множества, которые нельзя задать перечислением.

3. Множества задаются с помощью кругов (диаграмм) Эйлера.

В

Виды множеств.

1. Конечное множество.

Множество называется конечным, если оно состоит из конечного числа элементов.

А={а, в, с, d}. n=4 – количество элементов.

Количество элементов во множестве называется порядком этого множества.

Например: Множества бывают одноэлементные, двухэлементные и т.д.

2. Бесконечное множество.

Если множество состоит из бесконечного числа элементов, то его называют бесконечным.

Например: 1) - множество целых чисел 2)

3. Пустое множество.

Пустое множество не содержит элементов, Ø – обозначение пустого множества.

4. Упорядоченное множество.

Если каждому элементу множества присвоен порядковый номер, то множество называют упорядоченным.

- среди упорядоченных множеств эти множества разные, так как элементы стоят на разных местах.

Пусть а₁=3, а₂=8, тогда A={3;8} B={8;3}.

5. Подмножество множества.

Если каждый элемент множества А является элементом множества В, то множество А называют подмножеством множества В.

Записывают А В

Например: 1) А={1,2,3,} B={1,2,3,4,5} A B

2) A B

Замечание: Если элементы множества А не содержатся во множестве В , то записывают: А В.

А В

6) Равные множества.

Два множества называются равными, если они содержат одни и те же элементы. А={а, в}

В={а, в} Записывают: А=В.

Отношения

В математике для обозначения какой-либо связи между предметами или понятиями пользуются термином «Отношение».

В общем случае для понятия «отношения» используют символ ρ: Если объект «а» находится в отношении с объектом «в», пишут:

а ρ в.

Виды отношений:

1.Рефлексивность.

Отношение ρ на множестве А называется рефлексивным, если для любого элемента А : х ρ х

Например:

● число равно самому себе.

2. Симметричность

Отношение ρ на множестве А называется симметричным, если

х ρ у влечет у ρ х

Например:

● l₁ и l₂ – прямые, если l₁//l_{2 ,то} l₂//l₁

● Еслиl₁ l_{2 ,то} l₂ l₁

3.Транзитивность.

Отношение ρ называется транзитивным, если из х ρ у и у ρ z следует, что х ρ z

Например:

● 3 < 5 и 5 < 8 ,то 3 < 8

● 10 > 8 и 8 > 2_,то 10 2

● l₁ // l₂ и l₂ // l₃ ,то l₁ // l₃

● «А» -брат «В» и «В»- брат «С», то «А» брат «С»

4.Эквивалентность

Отношение ρ называется эквивалентным, если оно рефлексивно, симметрично и транзитивно.

Например: Отношения «равно» и «параллельно» являются отношениями эквивалентности.

№28

Операции над множествами.

1. Объединение (сумма)

Объединением или суммой множеств называется множество С, состоящее из элементов множества А и множества В, причем общие элементы учитываются только один раз.

Примеры: 1. А={1,2,3,4} В={3,4,5,6}

2 .

- заштрихованная часть.

3 .

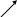
С

2. Пересечение

Пересечением множеств называется множество С, состоящее из всех элементов, принадлежащих одновременно и множеству А и множеству В.

Примеры:1. А={1,2,3,4} В={3,4.5,6}

2 .

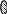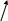
С

3. Разность

С=А\В

Разностью множеств А и В называется множество С, состоящее из тех элементов множества А, которые не содержатся во множестве В.

Примеры: 1. А={1,2,3,4} B={3,4,5,6} C=A\B={1,2}

2 .

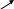
C=A\B

4. Симметрическая разность множеств

С=(А\В) (В\А)

Симметрической разностью множеств А и В называется множество С, состоящее из элементов, принадлежащих только множеству А и только множеству В.

А

В

5. Абсолютное дополнение множества

Абсолютным дополнением множества А называется множество , которое состоит из всех элементов, не принадлежащих множеству А.

Например: 1)

№29

Основные понятия теории графов.

1. Графом G=(V,X) называется совокупность двух конечных множеств: V – точек, называемых вершинами и X - линий, соединяющих некоторые пары точек, называемых ребрами. Обычно конечный граф изображают в виде диаграмм, где вершины – это точки, а ребра – это линии, их соединяющие.

2. Если на ребрах указано направление, то такой граф называют ориентированным или орграфом D=(V,X).

V=[v₁, v₂, … v_n]

X= [(x₁,x₂), (x₂,x₃), ….(x_n,x_n+1)]

3. Если x=(u,v) – ребро, то вершины u и v – концы этого ребра

Если x={u,v} – ориентированное ребро, то u – начало, v – конец ребра

4. Если x=(u,v) – ребро, то оно инцидентно к вершинам u и v, а вершина u и v инцидентны к ребру x.

5. Две вершины называются смежными, если они являются концами одного ребра.

6. Два ребра называются смежными, если они содержат одну общую вершину (выходят из одной вершины).

7. Петлей называется ребро, которое соединяет вершину саму с собой.

8. Кратными (параллельными) называются ребра, соединяющие две одинаковые вершины u и v (начало и конец, которых совпадают).

9. Количество кратных ребер называются кратностью ребра (u,v).

10. Граф, содержащий кратные ребра называется мультиграфом.

11. Граф, содержащий кратные ребра и петли, называется псевдографом.

12. Степенью вершины v deg (v) называется число ребер, выходящих из этой вершины .

13. Вершина v называется висячей, если deg (v) = 1.

14. Полустепень выхода вершины v deg_- (v) - это число ребер, выходящих из этой вершины.

15. Полустепень входа вершины v, deg₊ (v) - это число ребер, входящих в эту вершину. Вклад каждой петли и в deg_- (v) и в deg₊ (v) равен 1

16. Теорема 2. 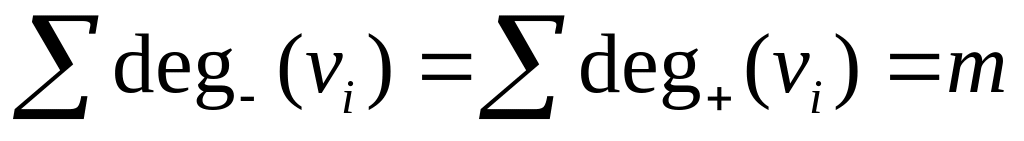суммы полустепеней входа и выхода равны между собой и равны числу ребер графа.

17. Граф называется пустым или нуль-графом, если он состоит из изолированных вершин.

18. Граф называется полным, если любые две различные вершины, соединены только одним ребром

19. Теорема 3. Степень вершины полного графа всегда на 1 меньше числа ребер.

20. Вершина называется четной (нечетной), если её степень четное (нечетное) число.

21. Теорема 4. Число нечетных вершин графа всегда четно.

№30