
- •8. Проверка гипотезы о математическом ожидании нормальной св при известной дисперсии
- •9. Проверка гипотезы о математическом ожидании нормальной св при неизвестной дисперсии.
- •10. Проверка гипотезы о равенстве дисперсий двух нормальных св.
- •11.Общая, каноническая, стандартная задача линейного программирования.
- •12. Симплексная форма злп.
- •13. Матричная форма симплексного метода. Критерии оптимальности плана и его отсутствия. Симплексные преобразования.
- •14. Геометрический способ решения системы линейных неравенств.
- •15. Графический метод решения стандартной злп
- •16. Взаимно двойственные злп.
- •17. Основные теоремы двойственности.
- •18. Транспортная задача и ее ранг.
- •19. Проверка опорного плана на оптимальность (метод потенциалов).
- •20. Переход от одного опорного плана к другому при решении транспортной задачи.
- •21. Двойственный симплекс-метод.
- •Методы решения матричной игры в смешанных стратегиях
Точечные оценки и их свойства.
Точечной оценкой Ɵ* параметра Ɵ называется числовое значение этого параметра, полученное по выборке объема n.
Оценка Ɵ* - случайная величина, меняющаяся от выборки к выборке.
Любую функцию, зависящую от выборочного значение Ɵ*= Ɵ*(x1, x2, … , xn) называют статистикой
Свойства:
Исследуемость Ɵ* параметра Ɵ называют неизменной, если M(Ɵ*)=Ɵ
Отдельная оценка Ɵ* не равняется Ɵ, но при многократном осуществлении выборки объема n среднее значение по всем выборкам будет равно Ɵ.
Разность M(Ɵ*)=Ɵ называется смещением или систематической ошибкой оценивания.
Эффективной оценки. Зачастую используют несколько несмещенных оценок одного и того же параметра.
Состоятельность. Каждая отдельная эффективная оценка не гарантирует того, что она даёт более точное значение исследуемого параметра, чем менее эффективное
2. Свойства выборочных оценок.
На начальном этапе исследования в качестве оценки той или иной числовой характеристики (M(x), D(x),…) берётся выборочная числовая характеристика. Затем исследуя эту оценку, её уточняют таким образом, чтобы она удовлетворяла условиям несмещения, состоятельности и т.д.
Свойства:
 -оценка
математического ожидания M(
-оценка
математического ожидания M(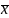 )=a.
)=a.
Пусть
D(x)
= υ
2
неизвестно. Покажем, что СВx
=
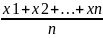 является
несмещенной оценкой M(x).
xi,
i
=
является
несмещенной оценкой M(x).
xi,
i
=
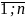 ,
является СВ, имеющая тот же закон
распределения, что и СВx.
Поэтому M(xi)=a,
D(xi)=υ2.
,
является СВ, имеющая тот же закон
распределения, что и СВx.
Поэтому M(xi)=a,
D(xi)=υ2.
Покажем,
что M(x)=a,
т.е.
-несмещенная
оценка M(x).
M(
)=M(
)=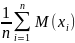 =
=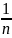 *n*a=a.
Таким образом
-несмещенная
оценка M(x)
*n*a=a.
Таким образом
-несмещенная
оценка M(x)
Рассмотрим свойства оценки дисперсии D(x) выборочной дисперсии.
S2=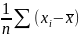 2.
Можно доказать, что M(S2)=
2.
Можно доказать, что M(S2)=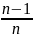 υ2.
Отсюда следует, что S2
– смещенная оценка υ2.
Введём несмещенную оценку дисперсии -
исправленную выборочную дисперсию.
υ2.
Отсюда следует, что S2
– смещенная оценка υ2.
Введём несмещенную оценку дисперсии -
исправленную выборочную дисперсию.
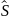 2=
2=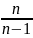 ;
S2=
;
S2=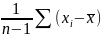 2.
Это оценка действительно будет
несмещенной, т.к. M(
2)
= M(
S2)=
M(s2)=
2.
Это оценка действительно будет
несмещенной, т.к. M(
2)
= M(
S2)=
M(s2)=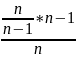 υ2=
υ2
υ2=
υ2
M( 2)= υ2
Можно
показать, что оценка является состоятельной.
Таким образом
2
– несмещенная и состоятельная оценка
υ2.
Можно ввести понятие исправленного
среднего квадратического отклонения.
=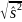 =
= )2.
Замечание: при объеме выборки n>30
различая между
2
и S2
незначительно.
)2.
Замечание: при объеме выборки n>30
различая между
2
и S2
незначительно.
Относительная частота. wi=w(x=xi)=
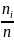 – несмещенная и состоятельная оценка
вероятности P(X=xi)
– несмещенная и состоятельная оценка
вероятности P(X=xi)Эмпирическая функция распределения. F*(x)=
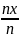 –
несмещенная и состоятельная оценка
функции распределения F(x)=P(X<x).
–
несмещенная и состоятельная оценка
функции распределения F(x)=P(X<x).
3. Интервальные оценки, их точность оценки.
После получения точечной оценки Ɵ* желательно иметь данные о надёжности такой оценки, о её точности. Поэтому, точечная оценка может быть дополненная интервальной оценкой – (Ɵ1, Ɵ2) внутри которого с посредством заданной вероятностью находится точное значение оцениваемого параметра Q. Такой интервал называется доверительным интервалом, а вероятность ɣ доверительно вероятной или надежной.
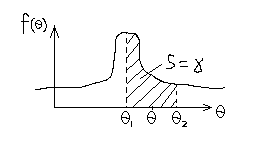
P(Ɵ1<Ɵ<Ɵ2)= ɣ
Длина доверительного интервала растет при увеличении надёжности ɣ и уменьшается увеличением объема выборки n. Обычно доверительный интервал выбирается симметрично относительно точечной оценки Ɵ*, т.е. доверительный интервал записывается в виде: (Ɵ*- υ, Ɵ*+ υ), тогда величина υ определяется из равенства (P|Ɵ - Ɵ*|< υ)= ɣ. Величина υ называется точностью оценки
4. Доверительный интервал для математического ожидания нормальной СВ при известной дисперсии.
Пусть количественный признак X генерируемой совокупности имеет нормальный закон распределения, X~N(a, υ2), а – неизвестная величина, υ2-известная. Необходимо найти по выборке объема n: x1,x2,...,xn доверительный интервал для математического ожидания a:
По данной выборке найдём точную оценку неизвестного параметра a: =
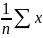 ;
;Составим СВ:
z=x-a/υ /n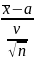 ,
,
z~N(0;1)Зададим надежность ɣ
Найдём zɣ такое, что P(|z|<zɣ)=ɣ
Изобразим на графике плотность распределения N(0;1)
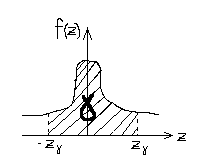
При
рассмотрении нормального законо
распределения было доказано, что
P(|z|<zɣ)
= 2Ф(zɣ).
Поэтому zɣ
можно найти из уравнения: 2Ф(zɣ)=ɣ
или Фzɣ
=
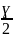
После нахождения zɣ по таблице функции Лапласса можно найти доверительный интеграл.
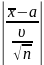 <zɣ
<zɣ
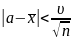 zɣ
zɣ
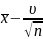 *
zɣ<a<
*
zɣ<a< *zɣ
*zɣ
Здесь
точность оценки
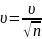 *zɣ
*zɣ
5. Доверительный интервал для математического ожидания нормальной СВ при неизвестной дисперсии.
В реальности истинное значение υ2 как правило неизвестно. Пусть X~N(a, υ2). a и υ2-неизвестные. Необходимо построить доверительный интервал для математического ожидания a:
Пусть извлечена выборка объма n: x1,x2,…,xn. Найдём точечные оценки параметров a,υ2:
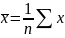 +
+
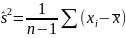 2
2
Рассмотрим статистику
 +
+
Которое имеет распределение Стьюдента с числом степеней свободы k=n-1.
Зададим надёжность ɣ
С помощью таблицы критических точек распределения Стьюдента найдём tɣ, которое удовлетворяет равенству
P(|T|<tɣ;k)= ɣ
После преобразований получим доверительный интервал
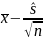 *
tɣ;k<a<
*
tɣ;k<a< *
tɣ;k
*
tɣ;k
6. Статистическая проверка гипотез. Ошибки первого и второго рода.
Статистической гипотезой называют гипотезу о виде закона распределения СВ или о параметрах известного закона распределения. Гипотеза Н0 подлежащая проверке называется нулевой (основной). Наряду с гипотезой Н0 рассматривается гипотеза Н1, которая применяется, если отклоняется гипотеза Н0. Такая гипотеза называется альтернативной (конкурирующей).
Сущность проверки статистической гипотезы заключается в том, чтобы установить согласуются ли выборочные данные и выдвинутая гипотеза.
При проверке гипотезы выборочные данные могут противоречить Н0, тогда Н0 отклоняется. Если же статистические данные согласуются с гипотезой Н0, то она не отклоняется.
Ошибка первого рода состоит в том, что будет отвергнута гипотеза Н0, в то время как она верна. Вероятность ошибки первого рода называется условием значимости и обозначается £.
Ошибка второго рода состоит в том, что будет принята гипотеза Н0, когда верна гипотеза Н1. Вероятность такой ошибки обозначается через ß.
7. Статистические критерии. Критическая область и ее нахождение.
Статистическую гипотезу проверяют на основе данных выборки. При этом используют специально подобранную СВ (статистику, критерий), распределение которой известно. Эту СВ в зависимости от её закона распределения обозначают так:
-
Z,
если она имеет N(0;1);
- T, если она имеет распределение Стьюдента;
- F, если она имеет распределение Фишера;
- X2, если она имеет распределение хи-квадрат.
В целях общности статистический критерий обозначим буквой k.
Таким образом, статистическим критерием называют СВк, которая служит для проверки статистической гипотезы. После выбора СВк множество её значений разбиваются на 2 попересекающихся подмножества:
- одно из них содержит значения k, при которых Н0 отклоняется (это критическая область);
- другое – при которых Н0 не отклоняется (область принятия гипотезы).
Основной принцип проверки статистических гипотез:
- Если k наблюдаемое (значение критерия k вычисляется по выборке) принадлежит критической области, то Н0 отклоняется и применяется гипотеза Н1.
- Если k наблюдаемое принадлежит области принятия гипотезы, но Н0 не отклоняется (принимается).
- Точки разделяются область принятия гипотезы с критической областью через критические точки
Нахождение критической области:
Пусть задан уровень значимости L для проверки гипотезы H0. Предположим, что используемая для проверки H0 статистика равна k. Для того, чтобы найти критические точки определим так, чтобы вероятность попадания СВк в критическую область равнялось L. В зависимости от вида гипотезы H1, критическая область может быть двусторонней или односторонней.
H1: Ɵ
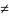 Ɵ0
Ɵ0
Тогда критическая область двусторонняя
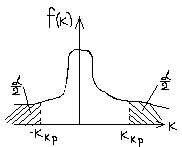
kкр. Определяется из равенства P(|k|>kкр.)=£
H1: Ɵ> Ɵ0
В этом случае критическая область правосторонняя
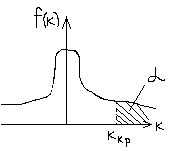
P(k>kкр.)=£
H1: Ɵ< Ɵ0
В этом случае критическая область левосторонняя
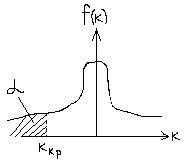
P(k<-kкр)=£
8. Проверка гипотезы о математическом ожидании нормальной св при известной дисперсии
Пусть генеральная совокупность Х распределена нормально, причем ее матем ожидание m неизвестно, а дипрессия q2 известна. Также есть основание предполагать, что m=m0. Тогда
H0: m=m0, H1:m m0, (H2:m>m0, H3:m<m0)
Для проверки Н0
извлекается выборка объема n:x1,x2,…,xn
и в качестве критерия строится статистика
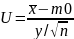 где
где
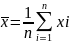 ,
y=
,
y=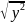 .
Доказано, что если Н0 справедлива, то
статистика U имеет
стандартизированное нормальное
распределение (U
.
Доказано, что если Н0 справедлива, то
статистика U имеет
стандартизированное нормальное
распределение (U N(0,1)).
N(0,1)).
Пусть в качестве альтернативной рассматривается гипотеза H1:m m0. Тогда критические точки
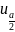 и
и
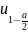 будут распределятся по таблице функций
Лапласа из условия
будут распределятся по таблице функций
Лапласа из условия
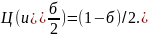
Если
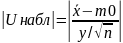 <
<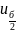 нет оснований для отклонения H0.
нет оснований для отклонения H0.
Если
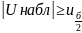 гипотеза Н0 отклоняется в пользу
альтернативной гипотезы Н1.
гипотеза Н0 отклоняется в пользу
альтернативной гипотезы Н1.
При H2:m>m0 критическую точку ua правосторонней крит области находят из равенства
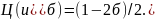
Если Uнабл < ua нет оснований для отклонения Н0
Если Uнабл ua Н0 отклоняется в пользу
Н1
ua Н0 отклоняется в пользу
Н1
При H3:m<m0 крит точка ua-1=-ua
Если Uнабл>u1-a нет оснований для отклонения Н0
Если Uнабл
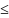 u1-a Н0
отклоняется в пользу Н1
u1-a Н0
отклоняется в пользу Н1
9. Проверка гипотезы о математическом ожидании нормальной св при неизвестной дисперсии.
Пусть
генеральная совокупность X имеет
нормальное распределение, причем ее
математическое ожидание m
и дисперсия
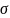 2
неизвестны. Данная ситуация более
реалистична по сравнению с предыдущей.
Пусть есть основания утверждать, что m
= m0.
Тогда строятся следующие гипотезы:
2
неизвестны. Данная ситуация более
реалистична по сравнению с предыдущей.
Пусть есть основания утверждать, что m
= m0.
Тогда строятся следующие гипотезы:
Н0: m = m0,
H1:m m0 (H2: m>m0; Н3: m <m0).
Для
Проверки Н0
извлекается выборка объема n:
x1
х2,...,
хn;
вычисляются выборочное среднее
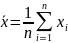 и исправленная выборочная
дисперсия
и исправленная выборочная
дисперсия
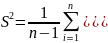 )2
| которой соответствует стандартное
отклонение
S
=
)2
| которой соответствует стандартное
отклонение
S
=
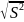 . Далее
строится следующая t-статистика:
. Далее
строится следующая t-статистика:

Имеющая при справедливости Н0 распределение Стьюдента с н=n-1 степенями свободы. Критическая область строится в зависимости от вида альтернативной гипотезы.
При Н0: m = m0 по таблице критических точек распределения Стьюдента по заданному уровню значимости
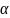 и числу степеней свободы н=n-1
критические точки
и числу степеней свободы н=n-1
критические точки
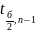 и
и
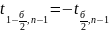
Если
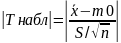 <
нет оснований для отклонения Н0.
<
нет оснований для отклонения Н0.
Если
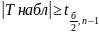 -Н0 отклоняют в пользу Н1.
-Н0 отклоняют в пользу Н1.
При H2: m>m0 определяют критическую точку tа,n-1 правосторонней критической области.
Если
Тнабл <
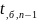 -нет оснований для отклонения Н0.
-нет оснований для отклонения Н0.
Если
Тнабл
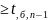 - Н0 отклоняют в
пользу Н2.
- Н0 отклоняют в
пользу Н2.
При H3 : m < т0 определяют критическую точку t1-а,n-1 = -tа,n-1 левосторонней критической области. Если Тнабл > —tб,n-1, — нет оснований для отклонения Н0.
Если Тнабл —tб,n-1 - Н0 отклоняют в пользу Н3.
10. Проверка гипотезы о равенстве дисперсий двух нормальных св.
Зачастую при сравнении двух экономических показателей на первый план выходит анализ разброса значений рассматриваемых СВ. Например, при решении вопроса об инвестировании в одну из двух отраслей остро стоит проблема риска вложений. При сравнении уровней жизни в двух странах среднедушевой доход может оказаться приблизительно равным. Сопоставив разброс в доходах, мы получаем более точное представление об интересуемом нас вопросе. Анализ, аналогичный описанному выше, целесообразно проводить путем сравнения дисперсий исследуемых СВ.
Пусть
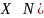 )
и
)
и
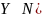 ),
причем их дисперсии
),
причем их дисперсии
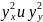 неизвестны. Выдвигается гипотеза о
равенстве дисперсий
неизвестны. Выдвигается гипотеза о
равенстве дисперсий
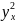 и
и
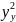 :
H0:
=
:
H0:
=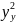 ,
H1:
,
H1:
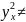 (
H2:
(
H2:
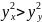 ).
).
По независимым выборкам
х1,х2,…,xn и у1,у2,…,yk
объемов n и k
соответственно определяются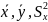 и
и
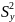 (для однозначности пусть
(для однозначности пусть
 .
В противном случае эти величины можно
переобозначить).
.
В противном случае эти величины можно
переобозначить).
В качестве критерия
проверки Н0 принимают СВ
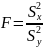 ,
определяемый отношением большей
исправленной выборочной дисперсии к
меньшей. Если Н0 верна, то данная статистика
F имеет F-
распределение Фишера с н1= n-1
и н2=k-1 степенями свободы.
,
определяемый отношением большей
исправленной выборочной дисперсии к
меньшей. Если Н0 верна, то данная статистика
F имеет F-
распределение Фишера с н1= n-1
и н2=k-1 степенями свободы.
При H1: по таблицам критических точек распределения Фишера по уровню значимости (а) и числам степеней свободы v1 и v2 определяется критическая точка
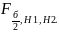
Если Fнабл<
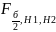 –нет оснований для отклонения Н0.
–нет оснований для отклонения Н0.
Если Fнабл≥ - Н0 отклоняется в пользу Н1.
При H2: определяется критическая точка
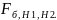
Если
Fнабл<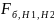 нет оснований для отклонения Н0.
нет оснований для отклонения Н0.
Если Fнабл ≥ - Н0 отклоняется в пользу Н2.
Заметим, что при проверке гипотезы о равенстве дисперсий в качестве альтернативной гипотезы в большинстве случаев используется гипотеза Н2.
