Методы решения матричной игры в смешанных стратегиях

Итак, если седловая точка отсутствует, решение игры проводят в смешанных стратегиях и решают следующими методами:

1. Решение игры через систему уравнений.  Если задана квадратная матрица nxn (n=m), то вектор вероятностей можно найти, решив систему уравнений. Этот метод используется не всегда и применим только в отдельных случаях (если матрица 2x2, то решение игры получается практически всегда). Если в решении получаются отрицательные вероятности, то данную систему решают симплекс-методом.

2. Решение игры графическим методом.  В случаях, когда n=2 или m=2, матричную игру можно решить графически.

3. Решение матричной игры симплекс-методом.  В этом случае матричная игра сводится к задаче линейного программирования.

27.

6	5	7
10	4	7
13	10	4
7	11	5

Решение:

A/B	B1	B2	B3	a = min(Ai)
A1	6	5	7	5
A2	10	4	7	4
A3	13	10	4	4
A4	7	11	5	5
b = max(Bi )	13	11	7	0

Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(ai) = 5, которая указывает на максимальную чистую стратегию A1.  Верхняя цена игры b = min(bj) = 7.  Что свидетельствует об отсутствии седловой точки, так как a ≠ b, тогда цена игры находится в пределах 5 <= y <= 7. Находим решение игры в смешанных стратегиях..  Математические модели пары двойственных задач линейного программирования можно записать так:  найти минимум функции F(x) при ограничениях:   6x₁+10x₂+13x₃+7x₄ >= 1   5x₁+4x₂+10x₃+11x₄ >= 1   7x₁+7x₂+4x₃+5x₄ >= 1   F(x) = x₁+x₂+x₃+x₄ = min   найти максимум функции Ф(y) при ограничениях:   6y₁+5y₂+7y₃ <= 1   10y₁+4y₂+7y₃ <= 1   13y₁+10y₂+4y₃ <= 1   7y₁+11y₂+5y₃ <= 1   Ф(y) = y₁+y₂+y₃ = max   Решим прямую задачу линейного программирования  симплексным методом, с использованием симплексной таблицы.  Определим минимальное значение целевой функции F(X) = x₁ + x₂ + x₃ + x₄ при следующих условиях-ограничений.   6x₁ + 10x₂ + 13x₃ + 7x₄≥1   5x₁ + 4x₂ + 10x₃ + 11x₄≥1   7x₁ + 7x₂ + 4x₃ + 5x₄≥1   Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).   6x₁ + 10x₂ + 13x₃ + 7x₄-1x₅ + 0x₆ + 0x₇ = 1   5x₁ + 4x₂ + 10x₃ + 11x₄ + 0x₅-1x₆ + 0x₇ = 1   7x₁ + 7x₂ + 4x₃ + 5x₄ + 0x₅ + 0x₆-1x₇ = 1   Поскольку задача решается на минимум и элементы единичной матрицы отрицательны, сведем задачу к нахождению максимума. Для этого умножим все строки на (-1) и будем искать первоначальный опорный план.   -6x₁-10x₂-13x₃-7x₄ + 1x₅ + 0x₆ + 0x₇ = -1   -5x₁-4x₂-10x₃-11x₄ + 0x₅ + 1x₆ + 0x₇ = -1   -7x₁-7x₂-4x₃-5x₄ + 0x₅ + 0x₆ + 1x₇ = -1   Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:

-6	-10	-13	-7	1	0	0
-5	-4	-10	-11	0	1	0
-7	-7	-4	-5	0	0	1

 Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом.   Решим систему уравнений относительно базисных переменных:   x₅, x₆, x₇,   Полагая, что свободные переменные равны 0, получим первый опорный план:   X1 = (0,0,0,0,-1,-1,-1)

План	Базис	B	x1	x2	x3	x4	x5	x6	x7
0	x5	-1	-6	-10	-13	-7	1	0	0
	x6	-1	-5	-4	-10	-11	0	1	0
	x7	-1	-7	-7	-4	-5	0	0	1
Индексная строка	F(X0)	0	1	1	1	1	0	0	0

 В столбце свободных членов есть отрицательные элементы. Используем двойственный симплекс-метод. Выберем из них наибольший по модулю, а в его строке – любой отрицательный. Взяв этот элемент в качестве разрешающего пересчитаем таблицу.   В качестве ведущего выберем столбец, соответствующий переменной x₁.   1-ая строка является ведущей.

План	Базис	B	x1	x2	x3	x4	x5	x6	x7
	x1	^1 /6	1	1^2/3	2^1/6	1^1/6	^-1 /6	0	0
	x6	^-1 /6	0	4^1/3	^5 /6	-5^1/6	^-5 /6	1	0
	x7	^1 /6	0	4^2/3	11^1/6	3^1/6	-1^1/6	0	1
Индексная строка	F(X)	^-1 /6	0	^-2 /3	-1^1/6	^-1 /6	^1 /6	0	0

 Представим расчет каждого элемента в виде таблицы:

B	x 1	x 2	x 3	x 4	x 5	x 6	x 7
^1 /6 : 1	1 : 1	1^2/3 : 1	2^1/6 : 1	1^1/6 : 1	^-1 /6 : 1	0 : 1	0 : 1
^-1 /6-(^1/6 • 0):1	0-(1 • 0):1	4^1/3-(1^2/3 • 0):1	^5 /6-(2^1/6 • 0):1	-5^1/6-(1^1/6 • 0):1	^-5 /6-(^-1/6 • 0):1	1-(0 • 0):1	0-(0 • 0):1
^1 /6-(^1/6 • 0):1	0-(1 • 0):1	4^2/3-(1^2/3 • 0):1	11^1/6-(2^1/6 • 0):1	3^1/6-(1^1/6 • 0):1	-1^1/6-(^-1/6 • 0):1	0-(0 • 0):1	1-(0 • 0):1
^-1 /6-(^1/6 • 0):1	0-(1 • 0):1	^-2 /3-(1^2/3 • 0):1	-1^1/6-(2^1/6 • 0):1	^-1 /6-(1^1/6 • 0):1	^1 /6-(^-1/6 • 0):1	0-(0 • 0):1	0-(0 • 0):1

    В столбце свободных членов есть отрицательные элементы. Используем двойственный симплекс-метод. Выберем из них наибольший по модулю, а в его строке – любой отрицательный. Взяв этот элемент в качестве разрешающего пересчитаем таблицу.   В качестве ведущего выберем столбец, соответствующий переменной x₄.   2-ая строка является ведущей.

План	Базис	B	x1	x2	x3	x4	x5	x6	x7
	x1	^4 /31	1	2^20/31	2^11/31	0	^-11 /31	^7 /31	0
	x4	^1 /31	0	^-26 /31	^-5 /31	1	^5 /31	^-6 /31	0
	x7	^2 /31	0	7^10/31	11^21/31	0	-1^21/31	^19 /31	1
Индексная строка	F(X)	^-5 /31	0	^-25 /31	-1^6/31	0	^6 /31	^-1 /31	0

 Представим расчет каждого элемента в виде таблицы:

B	x 1	x 2	x 3	x 4	x 5	x 6	x 7
^4 /31-(^1/31 • 0):1	1-(0 • 0):1	2^20/31-(^-26/31 • 0):1	2^11/31-(^-5/31 • 0):1	0-(1 • 0):1	^-11 /31-(^5/31 • 0):1	^7 /31-(^-6/31 • 0):1	0-(0 • 0):1
^1 /31 : 1	0 : 1	^-26 /31 : 1	^-5 /31 : 1	1 : 1	^5 /31 : 1	^-6 /31 : 1	0 : 1
^2 /31-(^1/31 • 0):1	0-(0 • 0):1	7^10/31-(^-26/31 • 0):1	11^21/31-(^-5/31 • 0):1	0-(1 • 0):1	-1^21/31-(^5/31 • 0):1	^19 /31-(^-6/31 • 0):1	1-(0 • 0):1
^-5 /31-(^1/31 • 0):1	0-(0 • 0):1	^-25 /31-(^-26/31 • 0):1	-1^6/31-(^-5/31 • 0):1	0-(1 • 0):1	^6 /31-(^5/31 • 0):1	^-1 /31-(^-6/31 • 0):1	0-(0 • 0):1

 В базисном столбце все элементы положительные.   Переходим к основному алгоритму симплекс-метода.

План	Aacen	B	x1	x2	x3	x4	x5	x6	x7	min
1	x1	^4 /31	1	2^20/31	2^11/31	0	^-11 /31	^7 /31	0	^4 /73
	x4	^1 /31	0	^-26 /31	^-5 /31	1	^5 /31	^-6 /31	0	-
	x7	^2 /31	0	7^10/31	11^21/31	0	-1^21/31	^19 /31	1	^1 /181
	F(X1)	^-5 /31	0	^-25 /31	-1^6/31	0	^6 /31	^-1 /31	0	0

28. Игры с природой. Матрица рисков.

Отличительная особенность игры с природой состоит в том, что в

ней имеется один активный игрок (игрок 1), а игрок 2 (природа) не дейст-

вует сознательно против игрока, а выступает как не имеющий

конкретной цели партнер по игре, который выбирает свои ходы случайным

образом. Термин «природа» характеризует некую объективную действи-

тельность.

Платежная матрица игры с природой имеет вид:

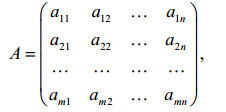
где aij – выигрыш игрока 1 при выборе им i-й стратегии, а игроком 2 – j-й

стратегии (i= 1,2,…,m; j = 1,2,…,n). Следует сразу отметить, что мажори-

рование стратегий в игре с природой имеет определенную специфику: ис-

ключать из рассмотрения можно лишь доминируемые стратегии 1-го игро-

ка. Если для всех j = 1,2,…,n выполняется условие aqj ≤ akj

, то q-ю стратегию игрока 1 можно не рассматривать и удалить из матрицы А. Столбцы

же, которые отвечают стратегиям игрока 2 (природы) исключать из матри-

цы игры А недопустимо, т.к. природа не стремится к выигрышу и для нее

нет целенаправленно выигрышных или проигрышных стратегий. С одной

стороны отсутствие противодействия упрощает игроку 1 задачу выбора

решения, но имеет место проблема обоснования выбора, так как гаранти-

рованный результат не известен.

Методы принятия решений в играх с природой зависят от характера

неопределенности в поведении игрока 2, т.е. от того, известны или нет ве-

роятности состояний (стратегий) природы. В первом случае мы имеем си-

туацию риска, а во втором – полной неопределенности. В силу этого ино-

гда игру с природой задают не в виде матрицы выигрышей, а в виде мат-

рицы рисков или матрицы упущенных возможностей

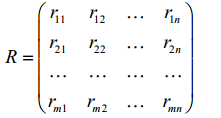
Риском rij игрока 1 при использовании им i-й стратегии и при j-м со-

стоянии среды (природы) называется разность между выигрышем, кото-

рый игрок получил бы, если бы он знал, что наступит j-е состояние среды и выигрышем, который игрок получит, не обладая этой информацией. Зная j-е состояние природы, игрок выбирает ту стратегию, при которой его вы-

игрыш максимален, т.е.

29. Критерий Бейеса-Лапласа. Критерий Лапласа.

Критерий Байеса - Лапласа

 (по ММ-критерию) каждый

. Критерий

Байеса - Лапласа (BL-критерий), напротив, учитывает каждое из возможных следствий.

Т огда для BL-критерия

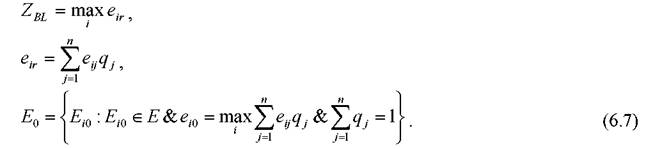
Правило выбора решения в соответствии с BL-критерием следующее.

дополняется еще одним столбцом, содержащим

 в строках которых стоит наибольшее значение eir этого

столбца.

При этом предполагается, что ситуация, в которой принимается решение, характеризуется следующими обстоятельствами:

известны и не зависят от времени;

решение реализуется (теоретически) бесконечное число раз;

- для малого числа реализаций решения допускается некоторый риск. При достаточно большом количестве реализаций среднее значение

постепенно стабилизируется. Поэтому при полной (бесконечной) реализации какой-либо риск практически исключен.

Исходная позиция при применении BL-критерия оптимистичнее, чем в случае ММ-критерия, однако она предполагает более высокий уровень информированности и достаточно длинные реализации.

30. Критерий Вальда. Критерий минимального риска Сэвиджа.

Минимизирует потери эффективности при наихудших условиях. Для оценки систем на основе данного критерия матрица эффективности должна быть преобразована в матрицу потерь (риска). Каждый элемент матрицы потерь определяется как разность между максимальным и текущим значениями оценок эффективности в столбце: Dkij = maxi kij - kij.                                          (10) После преобразования матрицы используется критерий минимакса: Оценим эффективность систем из приведенного примера в соответствии с данным критерием. Матрице эффективности будет соответствовать матрица потерь (таблица 3). Тогда К(а1) = 0,3; К(а2) = 0,2; K(a3) = 0,1. Оптимальное решение – система а1 . Критерий минимального риска отражает сожаление по поводу того, что выбранная система не оказалась наилучшей при определенном состоянии обстановки. Так, если произвести выбор системы а1, а состояние обстановки в действительности n3, то сожаление, что не выбрана наилучшая из систем (аз), составит 0,3. О критерии Сэвиджа можно сказать, что он, как и критерий Вальда, относится к числу осторожных критериев. По сравнению с критерием Вальда в нем придается несколько большее значение выигрышу, чем проигрышу. Таким образом, эффективность систем в неопределенных операциях может оцениваться по целому ряду критериев. На выбор того или иного критерия оказывает влияние ряд факторов: • природа конкретной операции и ее цель (в одних операциях допустим риск, в других — нужен гарантированный результат); • причины неопределенности (одно дело, когда неопределенность является случайным результатом действия объективных законов природы, и другое, когда она вызывается действиями разумного противника, стремящегося помешать в достижении цели); • характер лица, принимающего решение (одни люди склонны к риску в надежде добиться большего успеха, другие предпочитают действовать всегда осторожно). Устойчивость выбранного рационального варианта можно оценить на основе анализа по нескольким критериям. Если существует совпадение, то имеется большая уверенность в правильности выбора варианта.

31. Критерий Гурвица.

Минимаксное решение. Критерий Гурвица

Решения, принимаемые в условиях неопределенности, занимают весомую часть всего множества решений, принимаемых менеджерами. Но, как правило, на практике решения, принимаемые в условиях полной неопределенности, не встречаются. Для принятия решений предприятие должно собрать необходимый дополнительный объем релевантной информации и проанализировать ситуацию, либо принять решение на основе суждений, интуиции, анализа накопленного опыта руководителя. Для принятия оптимальных решений необходимо использовать научный подход при использовании различных методов.

К правилам принятия решений, при которых не учитывается численное значение вероятных исходов, относятся рассмотренные ранее максимаксное и максиминное решение, а также минимаксное решение и критерий Гурвица.

Минимаксное решение - это решение, при котором минимизируются максимальные потери. Это наиболее осторожный подход к принятию решений и наиболее учитывающий все возможные риски.

Правило минимакса (минимаксное правило возможных потерь) состоит в том, чтобы для каждого решения выбрать максимально возможные потери. Затем выбирается решение, которое ведет к минимальному значению максимальных потерь.

Под потерями учитываются не только реальные потери, но и упущенные возможности. При использовании данного правила внимание уделяется возможным потерям, чем доходам.

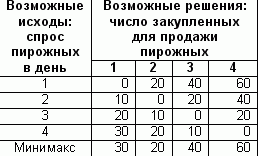
На основании данных предыдущего примера по реализации пирожных составим таблицу возможных потерь, которая дает представление о прибылях каждого исхода, потерянных в результате принятия неправильного решения (число закупленных единиц). 

Таблица возможных потерь за день 

Таблица заполняется следующим образом.

Если количество закупленных пирожных равняется спросу за день, то возможные потери равняются нулю.

Если было принято решение приобрести, например, 1 пирожное, а спрос в этот день составил 2 штуки, то упущенная выгода составит 1*(60-50)=10 руб. Это и есть возможные потери. Для 2 штук пирожных, которые могли бы продать, сумма возможных потерь составляет 20 руб., для 3-х пирожных - 30 руб.

В тех случаях, когда закупленная единица не была реализована, она приносит убыток 1* (50-30)=20, это тоже возможные потери.

Для каждого решения выбирается максимальное число возможных потерь. Это числа 30, 20, 40, 60 и определяем из них минимальное 20. Данное значение соответствует решению о закупке 2 штук. Следовательно, руководствуясь правилом минимакса, минимальная величина максимальных потерь возникает в результате закупки двух пирожных в день.

Критерий Гурвица (Hurwicz criterion)- это компромиссный способ принятия решений.

При выборе решения из двух крайностей: пессимистической оценкой по критерию максимина и оптимистической оценкой максимакса рационально придерживаться промежуточной позиции, граница которой регулируется показателем пессимизма-оптимизма µ, называемым степенью оптимизма в критерии Гурвица.

В соответствии с этим компромиссным решением будет линейная комбинация минимального и максимального выигрыша 

 

где 0 < µ < 1,

gnm - размер возможного дохода, который соответствует решениям при данных исходах.

Причем величину µ определяет исследователь или лицо, принимающее решение, при этом значению µ=1 критерию Гурвица соответствует правилу максимина (критерий Вальда), а значению µ =0 - правило максимакса (критерий Сэвиджа).

Критерий Гурвица заключается в том, что минимальному и максимальному результатам каждого решения присваивается "вес". Умножив результаты на соответствующие веса и суммируя их, лицо, принимающее решение, получает общий результат. Далее выбирается решение с наибольшим результатом.

Вернемся к предыдущему примеру и заполним таблицу по методу Гурвица.

Для четырех возможных решение были ранее получены максимаксное и максминное решения. Пусть вес минимального результата равен 0,4, следовательно, вес максимального - 0,6. 

Таблица возможных решений 

В данном примере критерий Гурвица свидетельствует в пользу решения о закупке одного пирожного, максимальная сумма составила 10. Очевидно, что при выборе других весов результат получается иным.

Поэтому к достоинству и одновременно недостатку критерия Гурвица относится необходимость присваивания весов возможным исходам: это позволяет учесть специфику ситуации, однако при этом всегда присутствует субъективный человеческий фактор - предпочтения аналитика.

32. Сетевые модели. Правила построения сетевой модели.

Правила построения сетевых моделей

Наиболее распространенным способом изображения СПУ являются сетевые модели в терминах работ и событий, где работы изображаются стрелками, а события — кружками. При построении сетевых моделей следует придерживаться следующих основных правил:

1. Строится трафарет событий.

2. Наносятся на трафарет последовательно все работы.

3. Просматриваются возможные варианты следования событий и работ, их табличная запись и формы изображения.

4. Всем стрелкам сетевого графика задают общее направление слева направо.

5. Не должно быть стрелок, которые ниоткуда не выходят и никуда не входят. 

 

6. Между одной парой событий можно изобразить только одну работу.

7. При необходимости изображения двух параллельно выполненных работ между двумя событиями 5 и 7  вводят дополнительное промежуточное событие 6 и фиктивную работу  с нулевой продолжительностью.

8. Из сети исключают тупиковые события, от которых не начинается ни одна работа, за исключением завершающего события комплекса.

9.  Проводят преобразование геометрии взаимного расположения работ и событий к виду, удобному для восприятия в целом, например устраняют пересечения работ.

10. Нумерацию событий проводят последовательно слева на право и сверху вниз.

В случае больших комплексов работ сначала строят частные сетевые графики ответственные исполнители, а затем формируют сводную модель комплекса путем их сшивания.

Установлено, что на листе бумаги размером 1,5x2 м можно разместить сетевой график, включающий до 1000 событий.

 

Правила построения сетевых моделей

 

1. Сеть вычерчивается слева направо, и каждое событие с большим порядковым номером изображается правее предыдущего. Общее направление стрелок, изображающих работы, также в основном должно быть расположено слева направо, при этом каждая работа должна выходить из события с меньшим номером и входить в событие с большим номером.

 

2. Два соседних события могут объединяться лишь одной работой. Для изображения параллельных работ вводятся промежуточное событие и фиктивная работа.

 

3. В сети не должно быть тупиков, т.е. промежуточных событий, из которых не выходит ни одна работа.

 

4. В сети не должно быть промежуточных событий, которым не предшествует хотя бы одна работа.

 

5. В сети не должно быть замкнутых контуров, состоящих из взаимосвязанных работ, создающих замкнутую цепь. Для правильной нумерации событий поступают следующим образом: нумерация событий начинается с исходного события, которому дается номер 1. Из исходного события 1 вычеркивают все исходящие из него работы, на оставшейся сети вновь находят событие, в которое не входит ни одна работа. Этому событию дается номер 2. Затем вычерчивают работы, выходящие из события 2, и вновь находят на оставшейся части сети событие, в которое не входит ни одна работа, ему присваивается номер 3, и так продолжается до завершающего события.

 

Продолжительность выполнения работ устанавливается на основании действующих нормативов или по экспертным оценкам специалистов. В первом случае временные оценки являются детерминированными (однозначными), во втором - стохастическими (вероятностными).

33. Расчет временных параметров сетевого графика.

Табличный метод расчета параметров сетевого графика

Пример. Определить временные параметры сетевого графика на рисунке, пользуясь табличным методом.  Решение: все вычисления будем заносить в таблицу 3.  Перечень работ и их продолжительность перенесем во вторую и третью графы. При этом работы следует записывать в графу 2 последовательно: сначала начиная с номера 1, затем с номера 2 и т.д.  В первой графе поставим число, характеризующее количество непосредственно предшествующих работ (КПР) тому событию, с которого начинается рассматриваемая работа. Так, для работы (5,10) в графу 1 поставим число 2, т.к. на номер 5 оканчиваются 2 работы: (1,5) и (3,5).  Таблица 3 – Табличный метод расчета сетевого графика

КПР	Код  Работы		Продолжительность работы		Ранние  сроки							Поздние  сроки									Резервы  времени
	( i,j)		t(i,j)		tрн(i,j)			tро(i,j)				tпн(i,j)				tпо(i,j)				Rп					Rс
1	2		3		4			5				6				7				8					9
1	2		3		4			5=3+4				6=7-3				7				8					9
0	(1,2)		5		0			5				2				7				2					0
0	(1,3)		7		0			7				0				7				0					0
0	(1,5)		4		0			4				11				15				11					3
1	(2,4)		0		5			5				7				7				2					2
1	(2,6)		8		5			13				12				20				7					0
1	(3,4)		0		7			7				7				7				0					0
1	(3,5)		0		7			7				15				15				8					0
1	(3,8)		7		7			14				13				20				6					0
1	(3,9)		11		7			18				12				23				5					1
2	(4,7)		12		7			19				7				19				0					0
2	(5,10)		5		7			12				15				20				8					2
1	(6,11)		7		13			20				20				27				7					7
1		(7,9)		0		19				19				23				23					4				0
1	(7,11)		8		19			27				19				27				0					0
1	(8,9)		0		14			14				23				23				9					5
1	(8,10)		0		14			14				20				20				6					0
1	(8,11)		4		14			18				23				27				9					9
3	(9,11)		4		19			23				23				27				4					4
2	(10,11)		7		14			21				20				27				6					6

Далее заполняем графы 4 и 5. Для работ, имеющих цифру 0 в графе 1, в графу 4 также заносятся нули, а их значения в графе 5 получаются в результате суммирования граф 3 и 4 (по формуле (2.4)). В нашем случае для работ (1,2), (1,3), (1,5) в графе  4  ставим 0, а в графе 5 -  0+5=5, 0+7=7, 0+4=4. Для заполнения следующих строк графы 4 , т.е. строк начиная с номера 2, просматриваются заполненные строки графы 5, содержащие работы, которые оканчиваются на этот номер, и максимальное значение переносится в графу 4 обрабатываемых строк. В данном случае такая работа одна - (1,2). Цифру 5 из графы  5 переносим в графу 4 для всех работ, начиная с номера 2, т.е. в две последующие строки с номерами (2,4) и (2,6). Для каждой из этих работ путем суммирования  значений граф 3 и 4 сформируем значение графы 5: t_р.о.(2,4)=0+5=5, t_р.о.(2,6)=8+5=13. Этот процесс повторяется до тех пор, пока не будет заполнена последняя строка таблицы. Графы 6 и 7 заполняются “обратным ходом”, т.е. “снизу вверх”. Для этого просматриваются строки, оканчивающиеся на номер последнего события, и из графы 5 выбирается максимальная величина, которая записывается в графу 7  по всем строчкам, оканчивающимся на номер последнего события (т.к. t_р(i)= t_п(i)).  В нашем случае t(11)=27. Затем для этих строчек находится содержание  графы 6 как разности граф 7 и 3 по формуле (2.7). Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 10. Для определения графы 7 этих строк (работы (8,10) и (5,10)) просматриваются все строчки, начинающиеся с номера 10. В графу 6 среди них выбирается минимальная величина, которая переносится в графу 7 по обрабатываемым строчкам. В нашем случае она  одна - (10,11), поэтому заносим в строчки (8,10) и (5,10) графы 7 цифру 20. Процесс повторяется до тех пор, пока не будут заполнены все строчки по графам 6 и 7.  Содержимое графы 8 равно разности граф 6 и 4 или граф 7 и 5 (формула (2.8).  Содержимое графы 9 вычисляется по формуле (2.9):  R_с(3,9)= t_р.н(9,11)- t_р.о.(3,9)=19-18=1.  Учитывая, что резерв времени имеют только события и работы, которые принадлежат критическому пути, получаем критический путь (1,3,4,7,11).

34. Критический путь. Резервы времени событий.

Критический путь определяет непрерывную последовательность критических операций, связывающих начальное и завершающее события сети. Критический путь задает все критические операции проекта. 

Расчет критического пути включает два этапа. Первый этап называется прямым проходом. Вычисления начинаются с начального события и продолжаются до тех пор, пока не будет достигнуто завершающее событие всей сети. Для каждого события j вычисляется одно число ESj , представляющее ранний срок его наступления (ранний срок окончания всех операций, входящих в событие j; ранний срок начала всех операций, выходящих из события j). На втором этапе, называемом обратным проходом, вычисления начинаются с завершающего события сети и продолжаются, пока не будет достигнуто начальное событие. Для каждого события i вычисляется число LFi , представляющее поздний срок его наступления (поздний срок окончания всех операций, входящих в событие i, поздний срок начала всех операций, выходящих из события i).

Первый этап. Если принять i = 0, т.е. считать, что номер исходного события сети равен нулю, то при расчете сети полагаем ES0 = 0. Обозначим символом Dij продолжительность операции (i,j). Тогда вычисления при прямом проходе выполняются по формуле: ESj = max{ESi + Dij}, где max берется по всем операциям, завершающимся в j-ом событии. Следовательно, чтобы вычислить ESj для события j, нужно сначала определить ESi начальных событий всех операций (i,j), входящих в событие j.

Второй этап начинается с завершающего события сети, для которого полагаем LFn ESn , где n – завешающее событие. Затем, для любого события i LFi = min{LFj - Dij}, где min берется по всем операциям, выходящим из i-го события.

Используя результаты вычислений первого и второго этапа, можно определить операции критического пути. Операция (i, j) принадлежит критическому пути, если она удовлетворяет следующим трем условиям: ESi = LFi; ESj = LFj; ESj - ESi = LFj - LFi = Dij. 

Эти условия означают, что между ранним сроком начала (окончания) и поздним сроком начала (окончания) критической операции запас времени отсутствует. В сетевой модели это отражается в том, что для критических операций числа, проставленные у начальных и конечных событий, совпадают, а разность между числом у конечного события и числом у начального события равна продолжительности соответствующей операции. Критический путь представляет собой непрерывную цепочку операций, соединяющую исходное событие сети с завершающим. 

После определения критического пути необходимо вычислить резервы времени для некритических операций. Очевидно, что резерв времени для критической операции должен быть равен нулю. Поэтому она и называется критической. Рассмотрим произвольную операцию (i,j).

Наиболее ранний возможный срок начала операции (i,j) – ESij – определяется при допущении, ESij = ESi, поскольку работа не может начаться раньше наступления предшествующего события i. Отсюда следует, что наиболее ранний возможный срок окончания операции (i,j): EFij = ESjj + Dij.

Наиболее поздний допустимый срок окончания работы (i,j) – LFij – определяется как самое позднее время завершения работы без задержки срока окончания всего проекта. Поскольку операция должна быть закончена не позднее наибольшего допустимого срока наступления последующего события j, то имеем LFij = LFj. Отсюда следует, что наиболее поздний допустимый срок начала работы (i,j) – LSij вычисляется следующим образом: LSij = LFij – Dij.

Резерв времени является показателем гибкости планирования сроков некритических работ в сетевой модели. Можно определить четыре показателя: полный, свободный, независимый и гарантированный резервы времени.

Полный резерв времени TFij для работы (i,j) представляет собой максимальную продолжительность задержки работы (i,j), не вызывающую задержки в осуществлении всего проекта. Он вычисляется как TFij = LSij – ESij = LFij – EFij.

Свободный резерв времени FFij для работы (i,j) является показателем максимальной задержки работы (i,j), не влияющей на начало последующих работ. Операции со свободным резервом уникальны, так как выполнение операции может откладываться, не влияя на ранний старт следующих операций. Изменение сроков операции со свободным резервом требует меньше координации с другими участками проекта. Он вычисляется как FFij = ESj – EFij .

Независимый резерв времени IFij. Не оказывает никакого влияния на предшествующие и последующие операции. Независимый резерв времени является удобным показателем свободы планирования сроков. Он представляет собой максимальную продолжительность задержки работы (i,j) без задержки последующих работ, если все предшествующие работы заканчиваются как можно позже, т.е. IFij = max {0, ESi – (LFi + Dij)}.

Гарантированный резерв времени SFij – это максимально возможная задержка работы, не влияющая на окончательный срок выполнения проекта, если предшествующие работы выполняются с запаздыванием: SFij = LFij – (LFi + Dij).

Только критические операции должны иметь нулевой полный резерв времени. Когда полный резерв равен нулю, свободный резерв также должен быть равен нулю. Однако обратное неверно, поскольку свободный резерв некритической операции также может быть нулевым.

Необходимо учитывать, что при вычислении полного резерва времени принимается неявное допущение, согласно которому все предшествующие работы должны выполняться как можно раньше, чтобы обеспечить полный резерв времени для данной работы. Следовательно, практически невозможно для каждой работы реализовать собственный полный резерв времени.

Свободный резерв времени для определенной работы не может превышать полный резерв.

Различные показатели резерва времени помогают распределять имеющиеся ресурсы для каждой работы. При наличии резерва времени имеется некоторая свобода распределения ресурсов.

35. Задача об оптимальном распределении инвестиций. Принцип Беллмана.