20. Переход от одного опорного плана к другому при решении транспортной задачи.

Числа и называют потенциалами. В распределительную таблицу добавляют строку и столбец . Потенциалы и находят из равенства , справедливого для занятых клеток. Одному из потенциалов дается произвольное значение, а остальные потенциалы определяются однозначно. Если известен потенциал , то , если известен потенциал , то .

Обозначим , которую называют оценкой свободных клеток. Если все оценки свободных клеток , то опорное решение является оптимальным. Если хотя бы одна из оценок , то опорное решение не является оптимальным и его можно улучшить, перейдя от одного опорного решения к другому.

Наличие положительной оценки свободной клетки ( ) при проверке опорного решения на оптимальность свидетельствует о том, что полученное решение не оптимально и для уменьшения значения целевой функции надо перейти к другому опорному решению. При этом надо перераспределить грузы, перемещая их из занятых клеток в свободные. Свободная клетка становится занятой, а одна из ранее занятых клеток - свободной.

Для свободной клетки с строится цикл (цепь, многоугольник), все вершины которого, кроме одной, находятся в занятых клетках; углы прямые, число вершин четное. Около свободной клетки цикла ставится знак (+), затем поочередно проставляют знаки (-) и (+). У вершин со знаком (-) выбирают минимальный груз, его прибавляют к грузам, стоящим у вершин со знаком (+), и отнимают от грузов у вершин со знаком (-). В результате перераспределения груза получим новое опорное решение. Это решение проверяем на оптимальность и т.д. до тех пор, пока не получим оптимальное решение.

21. Двойственный симплекс-метод.

Смысл двойственного симплекс-метода заключается в том, что вместо прямой задачи решают двойственную при помощи обычного симплекс-метода. Затем по решению двойственной задачи находят оптимальное решение прямой. Для этого устанавливается взаимнооднозначное соответствие между переменными прямой и двойственной задач. Исходным переменным прямой задачи ставятся в соответствие дополнительные переменные двойственной, а дополнительным переменным исходной задачи ставятся в соответствие исходные переменные задачи прямой.

Пусть решена двойственная задача и получена оптимальная симплекс-таблица. Оптимальное решение прямой задачи определяется коэффициентами F-строки. Переменные прямой задачи приравниваются к коэффициентам при соответствующих им небазисных переменных в F-строке оптимальной симплекс-таблицы двойственной задачи. Остальные переменные равны нулю. Наиболее целесообразно применять двойственный симплекс-метод в случае, когда число ограничений прямой задачи намного больше, чем число неизвестных, а также в задачах целочисленного программирования.

Пример 1. Применяя двойственный симплекс-метод, решить следующую задачу:

F(x)=6x₁+12x₂ (min)

-2x₁+3x₂≤6;

4x₁-3x₂≤12;

3x₁+x₂≥3;

x₁≤2;

x_1,2≥0;

Приводим неравенства задачи к знаку ≥, умножая первое, второе и четвертое ограничения на (-1); тогда модель двойственной задачи будет иметь вид:

F(x)=-6y₁-12y₂+3y₃-2y₄ (max)

2y₁-4y₂+3y₃-y₄≤6

-3y₁+3y₂+y₃≤12

y₁≥0, y₂≥0, y₃≥0, y₄≥0.

Решение двойственной задачи осуществляем обычным симплекс-методом (табл. 1 и 2).

Таблица 1

базисные переменные	Свободные члены	Небазисные переменные
		y1	y2	y3	y4
y5	6	2	-4	3	-1
y6	12	-3	3	1	0
F	0	6	12	-3	2

Таблица 2

базисные переменные	Свободные члены	Небазисные переменные
		y1	y2	y5	y4
y3	2	2/3	-4/3	1/3	-1/3
y6	10	-11/3	13/3	-1/3	1/3
F	6	8	8	1	1

Решение, соответствующее табл. 2, является оптимальным. Запишем соответствие между переменными прямой и двойственной задач. Если ограничения прямой задачи приводить к виду равенств, то в качестве дополнительных появятся переменные x₃, x₄, x₅, x₆.

Тогда

В F-строке расположены коэффициенты при небазисных переменных y₁, y₂, y₅, y₄. Найдем оптимальное решение прямой задачи:

x₃ = 8; x₄ = 8; x₁ =1; x₆ =1.

Переменная x₅ , соответствующая y₃, и x₂, соответствующая y₆ , равны нулю.

min F( y) = max F(x) = 6.

Таким образом, решая симплексным методом одну из пары двойственных задач, автоматически получаем решение другой.

22. Целочисленное программирование. Методы отсечения.

Специфика задач целочисленного программирования заключается в том, что на переменные x_i и функцию цели F(x) налагается дополнительное ограничение – условие целочисленности. Целочисленное программирование иногда называют дискретным программированием. Если требование целочисленности распространяется не на все переменные, а только на часть из них, то задача называется частично целочисленной.

В большинстве случаев целочисленные задачи сильно отличаются от своих непрерывных аналогов и требуют для решения специальных методов. Условно методы решения задач целочисленного программирования можно разделить на три основных группы: методы отсечения; комбинаторные методы; приближенные методы.

Процедура решения задачи методом отсечения осуществляется следующим образом:

1. Решается задача линейного программирования с отброшенным условием целочисленности. Если в полученном оптимальном решении хотя бы одна переменная или функция цели являются дробными, то переходят ко второму шагу.

2. Строятся дополнительные линейные ограничения, отсекающие от ОДЗП ту её часть, в которой содержится оптимальное решение и не содержится ни одного целочисленного решения.

3. В исходную задачу включается дополнительное ограничение и применяется симплекс-процедура. Если же найденное оптимальное решение опять будет дробным, то формируется новое дополнительное ограничение и процесс вычислений повторяется.

Способы построения дополнительных линейных ограничений известны как алгоритмы Гомори. Они различны для полностью и частично целочисленных задач и обеспечивают решение задачи за конечное число шагов.

23. Метод Гомори

Алогоритм Гомори включает в себя следующие этапы:

1. Решается задача линейного программирования без учета целочисленности.

2. Среди дробных чисел выбирается элемент с наибольшей дробной частью и составляется дополнительное ограничение.

3. Неравенство преобразуется в уравнение путем введения дополнительной неортицательной переменной.

4. Полученная задача решается двойственным симплекс-методом.

24. Матричные игры. Платежная матрица.

Игра– это математическая модель реальной конфликтной ситуации.

Конфликтная ситуация двух игроков называется парной игрой. Парную игру с нулевой суммой удобно исследовать, если она описана в виде матрицы. Такая игра называется матричной; матрица, составленная из чисел a_ij, называется платежной.

0	-1	-2
1	0	4
2	1	0

Математической моделью антагонистической игры является матричная игра с матрицей A, в которой ходы (стратегии) игрока A расположены по строкам, а ходы (стратегии) игрока B расположены по столбцам. В самой матрице записаны выигрыши игрока A при соответствующих ходах игроков A и B (отрицательный выигрыш – это проигрыш).

25. Матричная игра с седловой точкой. Нижняя и верхняя цены игры. Седловая точка.

Конец формы

В таблице представлены варианты решения игры, заданной платежной матрицей А.

	Наличие седловой точки	Отсутствие седловой точки
Тип стратегии	Чистая стратегия	Смешанная стратегия
Метод решения	Решение найдено	1. Через систему уравнений. 2. Графический метод. 3. Использование симплекс-метода.

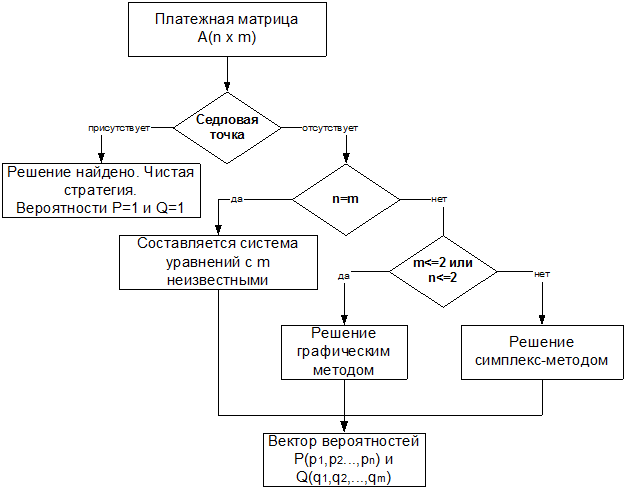
Описание алгоритма:

1. На основании анализа платёжной матрицы следует определить, существуют ли в ней доминируемые стратегии, и исключить их.

2. Найти верхнюю и нижнюю цены игры и определить, имеет ли данная игра седловую точку (нижняя цена игры должна быть равна верхней цене игры).

3. Если седловая точка существует, то оптимальными стратегиями игроков, являющимися решением игры, будут их чистые стратегии, соответствующие седловой точке. Цена игры равна верхней и нижней цены игры, которые равны между собой.

4. Если игра не имеет седловой точки, то решение игры следует искать в смешанных стратегиях. Для определения оптимальных смешанных стратегий в играх m × n следует использовать симплекс-метод, предварительно переформулировав игровую задачу в задачу линейного программирования.

Представим алгоритм решения матричной игры графически.

26. Смешанные стратегии. Цена игры.