14. Геометрический способ решения системы линейных неравенств.

A1x1+a2x2≤b1 (10)

(x1,x2) будем рассматривать как точку на координатной плоскости. Совокупность решения (х1,х2) неравенства 10 называется областью решения данного неравенства.

Теорема: областью решения линейного неравенства с двумя переменными (10) является одна из полуплоскостей на который вся плоскость делится прямой а1х1+а2х2=в1, включающая и эту прямую, а другая полуплоскость с той же прямой является областью решений неравенства а1х1+а2х2 в1

Область решений линейного неравенства является выпуклой(она с любыми двумя точками содержит и отрезок соединяющий эти точки)

Теорема: пересечение любого числа выпуклых областей, есть область выпуклая. Отсюда следует что областью решений системы лин неравенств с двумя переменными явл выпуклая многоугольная область как пересечение конечного числа полуплоскостей.

15. Графический метод решения стандартной злп

Этот метод часто используется при решении задач, в которых только две неизвестных величины.

Небольшая фабрика изготовляет два вида красок: INT - для внутренних работ и EXT - для наружных работ. В производстве красок используются два исходных продукта А и В. Из-за малой площади склада максимально возможные суточные запасы этих продуктов равны 6 т. и 8 т. соответственно. На производство 1 тонны краски INT расходуется 1 тонна продукта А и 2 тонны продукта В, а на изготовление 1 тонны краски EXT идет 2 тонны продукта А и 1 тонна продукта В. Фабрика продает краску по цене 3 тыс. долл. за тонну краски INT и 2 тыс. долл. за тонну краски EXT. Исходные данные удобно свести в таблицу:

Исходные продукты	Расход продукта на 1 т. краски		Запас продуктов
	INT	EXT
A	1	2	6
B	2	1	8
Цена 1т. краски	3 тыс. долл.	2 тыс. долл.

Изучение рынка сбыта показало, что суточный спрос на краску EXT никогда не превышает спрос на краску INT, более чем на 1 тонну. Какое количество краски каждого вида должна производить фабрика в сутки, чтобы доход от реализации продукции был максимален?

Построим математическую модель задачи. Для этого надо определить переменные задачи, целевую функцию и ограничения, которым удовлетворяют переменные. Обозначим через x₁ - планируемый суточный объем производства краски INT, а через x₂ - суточный объем производства краски EXT. Целевая функция f(x) будет выражать суточный доход от продажи краски, равный 3x₁ + 2x₂ (тыс. долл.). Этот доход подлежит максимизации

f(x)= 3x₁ + 2x₂  max.

Построим ограничения задачи, связанные с ограниченными запасами продуктов А и В. На производство краски INT в количестве x₁ (т) будет использовано 1x₁ (т) продукта А, а на производство краски EXT в объеме x₂ (т) будет затрачено 2x₂ (т) продукта А. Поскольку суточный запас продукта А равен 6 т., то расход продукта А на изготовление красок двух видов не может превышать в сутки этой величины: 1x₁+ 2x₂  6. Аналогично получим ограничение, связанное с запасом продукта В: 2x₁+1x₂  8. Ограничение по соотношению спроса на краски можно описать неравенством: x₂ - x₁  1. Учитывая естественные условия неотрицательности объемов выпуска продукции, окончательно получим следующую задачу линейного программирования

f(x) = 3 x₁ + 2 x₂  max (1.1)

1 x₁ + 2 x₂  6, (1.2)

2 x₁ + 1 x₂  8, (1.3)

- x₁ + x₂  1, (1.4)

x₁  0, x₂  0. (1.5)

Построим множество планов задачи, описываемое ограничениями (1.2)-(1.5). Рассмотрим первое неравенство. Оно задает некоторую полуплоскость, расположенную по одну сторону от граничной прямой

p₁: 1x₁+2x₂=6

Построим эту прямую на плоскости с координатными осями x₁ и x₂. Для проведения прямой достаточно знать две ее точки. Проще всего найти точки пересечения прямой с осями координат. Полагая x₁ = 0, из уравнения прямой получим x₂ = 3, а при x₂ = 0 найдем x₁ = 6. Таким образом прямая p₁ пройдет через точки (0,3) и (6,0). Чтобы определить, по какую сторону от прямой расположена искомая полуплоскость, достаточно подставить в неравенство (1.2) координаты любой точки плоскости. Если прямая не проходит через начало координат, то удобнее всего взять точку (0, 0). Очевидно, что в этой точке неравенство (1.2) строго выполняется (1* 0 + 2* 0 < 6), значит полуплоскость, определяемая этим неравенством, лежит ниже прямой p₁, включая в себя начало координат. Искомую полуплоскость отметим штриховкой (рис.1.1).

Аналогично построим полуплоскость, задаваемую неравенством (1.3). Для этого нанесем на координатную плоскость граничную прямую

p₂: 2x₁+x₂=8,

найдя ее точки пересечения с осями координат: (0,8) и (4,0).

Подставляя координаты точки (0,0) в неравенство (2.3), видим, что начало координат лежит в искомой полуплоскости (2* 0 + 1* 0 < 8), значит все точки, удовлетворяющие неравенству (2.3), расположены левее прямой p₂. Отметим эту область штриховкой (рис.1.1).

Точки, задаваемые ограничением (4), находятся ниже прямой

p₃: -x₁+x₂=1,

проходящей через точки (0, 1) и (-1, 0).

Наконец, условия неотрицательности: x₁  0, x₂ 0 задают все точки первой четверти, что также отметим штриховкой.

Выделяя теперь точки плоскости, удовлетворяющие всем ограничениям задачи (1.1)-(1.5), то есть расположенные одновременно во всех заштрихованных полуплоскостях, получаем множество планов X. Оно представляет собой многоугольник (в данной задаче - пятиугольник). Его стороны лежат на прямых, уравнения которых получаются из исходной системы неравенств (1.2)-(1.5) заменой знаков неравенств на строгие равенства.

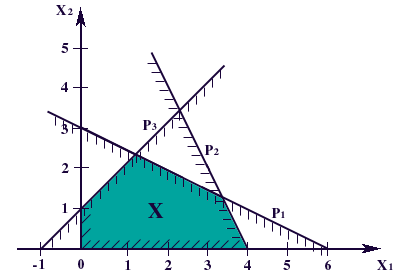
Рис. 1.1

Для графического представления целевой функции введем понятие линии уровня (изолинии функции).

Определение. Линией уровня (изолинией) функции f(x) называется множество точек x = (x_1, x₂), в которых она принимает одно и то же постоянное значение f(x) = h, где h - некоторое число. Для линейной функции двух переменных f(x) = c₁ x₁ + c₂ x₂ линия уровня, соответствующая числу h, будет представлять прямую с уравнением

c₁ x₁ + c₂ x₂ = h (1.6)

При изменении числа h будем получать семейство линий уровня (параллельных прямых) с одним и тем же направляющим вектором c = =(c₁, c₂₎, перпендикулярным всем прямым. Известно, что вектор c = (c₁, c₂) для линейной функции f(x) = c₁ x₁ +c₂ x₂ указывает направление ее возрастания. Геометрически это означает, что при параллельном перемещении прямой (1.6) в направлении целевого вектора c значение целевой функции возрастает.

Построим линии уровня целевой функции f(x) = 3x₁ + 2 x₂ в нашей задаче. Их уравнения будут иметь вид 3x₁ + 2 x₂ = h. Они задают семейство параллельных прямых, зависящих от параметра h. Все прямые перпендикулярны целевому вектору c = (3, 2), составленному из коэффициентов целевой функции, поэтому для построения семейства линий уровня целевой функции достаточно построить ее целевой вектор, и провести несколько прямых, перпендикулярных этому вектору. Линии уровня будем проводить на множестве планов X, помня при этом, что при параллельном перемещении прямых в направлении целевого вектора c = (3, 2₎ значение функции f(x)= 3x₁ + 2x₂ будет возрастать. Поскольку в задаче оптимальный план должен доставлять целевой функции максимально возможное значение, то для решения задачи графически надо среди всех точек x = (x_1, x₂) множества планов X найти такую точку x* = (x₁*_, x₂*), через которую пройдет последняя линия уровня в направлении целевого вектора c = (3,2₎. Из рисунка 1.2 видно, что искомой точкой будет точка, лежащая в вершине множества X, образованной пересечением прямых p₁ и p₂. Решая систему уравнений, описывающих эти прямые найдем оптимальный план x₁* = 3 ¹/₃, x₂* = 1 ¹/₃. При этом максимальное значение целевой функции будет равно f(x*) = 12 ²/₃. Таким образом, ежесуточно фабрика должна производить 3 ¹/₃ тонн краски INT и 1 ¹/₃ тонн краски EXT, получая при этом доход 12 ²/₃ тыс. долларов.

x₁ + 2 x₂ = 6,

2 x₁ + x₂ = 8,