
- •Билет 19 поверхностный интеграл.
- •Билет 20 вычисление поверхностного интеграла.
- •Билет 21. Формула остроградского
- •Билет 22. Понятие дифф уравнения, общее решение, задача коши
- •3.5.1. Понятие дифференциального уравнения
- •Задача Коши
- •Билет 23. Понятие дифа 1го порядка, уравнения с разделяющимися переменными.
- •Решение. Разделим переменные
- •Интегрируем обе части, полученного равенства
- •Возвращаясь к переменной у , получаем
- •Билет 24. Однородные уравнеиня 1го порядка
Билет 19 поверхностный интеграл.
Пусть в каждой точке гладкой ориентированной простой поверхности σ определена векторная функция:
![]() (M)
= P(M)
(M)
= P(M)![]() + Q(M)
+ Q(M)![]() + R(M)
+ R(M)![]() с непрерывными проекциями P,
Q, R.
с непрерывными проекциями P,
Q, R.
Разобьём
поверхность σ произвольным образом на
элементарные части ∆σ1, ∆σ2,…∆σn
с диаметрами: d1,
d2, …dn.
Наибольший из диаметров обозначим через
dM.
На каждом элементе возьмем произвольную
точку MK
и составим интегральные суммы вида:
 (1)
(1)
![]() 0(Mk)-единичный
вектор нормали к поверхности в точке
Мk.
0(Mk)-единичный
вектор нормали к поверхности в точке
Мk.
Обозначим через αk, βk и γk углы, образуемые вектором 0(Mk) с осями координат (направляющие углы). Тогда:
0(Mk)
= cos αk![]() + cos βk
+ cos βk![]() + cos γk
+ cos γk![]() и
и
(![]() (Mk),
0
(Mk))
=
(Mk),
0
(Mk))
=
=P(Mk) cos αk + Q(Mk) cos βk + R(Mk) cos γk
Интегральная сумма (1) распадается на три однотипные суммы:
Jn
=![]() [P(Mk)
cos αk
+Q(Mk)
cos βk
+R(Mk)
cos γk
]∆σK
=
[P(Mk)
cos αk
+Q(Mk)
cos βk
+R(Mk)
cos γk
]∆σK
=
= JnI + JnII + JnIII . (2)
Если существует предел интегральных сумм (1) при dM→0, не зависящий ни от способа разбиения поверхности на части, ни от выбора промежуточных точек МК, то он называется поверхностным интегралом второго рода от векторной функции = {P, Q, R,} по выбранной стороне поверхности.
Обозначается:
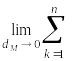 (
(Mk),
(
(Mk),![]() (Mk))∆σk
=
(Mk))∆σk
=
=
![]() (
(MK),
(MK))∆σK
(3)
(
(MK),
(MK))∆σK
(3)
или
 [P(хk,
yk,
zk)
cos αk
+ Q(хk,
yk,
zk
) cos βk
+
[P(хk,
yk,
zk)
cos αk
+ Q(хk,
yk,
zk
) cos βk
+
+ R(хk, yk, zk ) cos γk] = [P(хk, yk, zk) cos αk +
+ Q(хk, yk, zk ) cos βk + R(хk, yk, zk ) cos γk] dσ (4)
Свойства поверхностных интегралов:
1.
Из определения поверхностного интеграла
следует, что если изменить ориентацию
поверхности, то
![]() +
заменится на
+
заменится на
![]() -,
а т.к.
+
= -
, то и поверхностный интеграл изменит
знак на противоположный;
-,
а т.к.
+
= -
, то и поверхностный интеграл изменит
знак на противоположный;
( , +)dσ = - ( , )dσ
2. Если поверхность σ разбить на части σ1 и σ1, то:
(
,
)dσ
=
![]() (
,
)dσ
+
(
,
)dσ
+
![]() (
,
)dσ
(
,
)dσ
Остальные свойства поверхностных интегралов также совершенно аналогичны свойствам всех интегралов.
Замечание 1: Поверхность σ может быть замкнутой. В этом случае, обычно выбирают внешнее направление нормали, а интеграл обозначается;
![]() (
,
)dσ
(
,
)dσ
Замечание 2: Так как cosγ dσ = dxdy, cosβ dσ = dxdz, cosγdσ = dydz – проекции элемента поверхности на соответствующие координатные плоскости, то (4) можно записать в виде:
![]() (
(M),
(M))dσ
=
(Pdydz
+ Qdxdz + Rdxdy)
(5)
(
(M),
(M))dσ
=
(Pdydz
+ Qdxdz + Rdxdy)
(5)
(проекции положительны, если углы α, β, γ – острые, если они тупые, то проекции отрицательны).
Поверхностный интеграл (4) или (5) можно рассматривать как сумму трёх соответствующих простых интегралов от функций P, Q, R:
[Pcosα
+ Qcosβ
+ Rcosγ]dσ
=![]()
= Pcosαdσ + Qcosβdσ + Rcosγdσ (6)
Обозначим: Pcosαdσ = J1, Qcosβdσ = J2,
Rcosγdσ = J3
Каждый из интегралов в правой части является пределом своей
частной интегральной суммы в (2).
Пусть, например, поверхность σ такая, что каждая прямая параллельная оси Oz пересекает ее только в одной точке. Тогда её уравнение можно записать в виде: z = ƒ(x,y), где (x,y) D1, а D1, – проекция поверхности σ на плоскости Oxy. Тогда:
J3 = R(x, y, z)cosγdσ =
=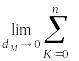 R(xk,yk,zk)
cosγkΔσk
R(xk,yk,zk)
cosγkΔσk
=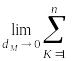 R(xk,yk,zk)Δ
Sxy(k)
=
R(xk,yk,zk)Δ
Sxy(k)
=
=
±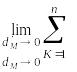 R[xk,yk,
ƒ(xk,yk
)]| Sxy(k))
| ;
R[xk,yk,
ƒ(xk,yk
)]| Sxy(k))
| ;
Так как zk = ƒ(xk,yk ) и Δ Sxy(k)=cosγk Δσk
Знак (-) берут тогда, когда угол γk тупой (cosγk<0)( нормаль к поверхности с осью Оz образует тупой угол), а знак (+) когда этот угол острый (cosγk>0).
dM - максимальный диаметр частичных областей ∆σ1, ∆σ2…∆σn поверхности σ, а d'M - максимальный диаметр частичных областей с площадями ΔS1, ΔS2,…ΔSn области D1 на плоскости Оху. Если d'M→0, то и dM→0 (поверхность гладкая).
Полученная сумма является интегральной для двойного интеграла от функции двух переменных R[x,y, ƒ(x,y )]по области D1. Таким образом,
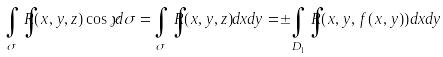 Поверхностный
интеграл выражен через двойной. Для
вычисления интеграла J2
надо уравнение поверхности σ разрешить
относительно y:
y = φ(х,
z), а поверхность σ
проектировать на плоскость Охz
(обл D2):
Поверхностный
интеграл выражен через двойной. Для
вычисления интеграла J2
надо уравнение поверхности σ разрешить
относительно y:
y = φ(х,
z), а поверхность σ
проектировать на плоскость Охz
(обл D2):
 А
для вычисления интеграла J3
уравнение поверхности представляем в
виде x = ψ(y,
z), а поверхность
проектируем на плоскость Oyz
(обл. D3):
А
для вычисления интеграла J3
уравнение поверхности представляем в
виде x = ψ(y,
z), а поверхность
проектируем на плоскость Oyz
(обл. D3):
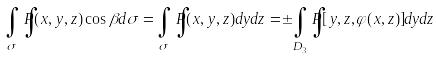
Знаки (+) берут если углы β и α острые, если тупые то берут (-).
Замечание1: интеграл (6) можно свести к двойному, выразив направляющие косинусы и dσ с помощью уравнения поверхности.
Замечание 2. Если поверхность σ не является простой или гладкой, то её разбивают на участки, являющиеся простыми и гладкими.
