Рис.
41.
Разобьем поверхность на части σ0 и σ1. Заданный интеграл представим в виде суммы трех интегралов:
I= x4dydz + dxdz + zdxdy =
= x4dydz + dxdz + z dxdy= I1 +I2 +I3.
Рассмотрим последовательно каждый из них.
1.
I1 =
Рис. 42. Рис. 43.
т.к. для σ1 cosα=0, то
,
I1 =
σ0:
x =
(передняя и задняя поверхности σ01
и σ02). Обе они проектируются
на область D2 в
плоскости Oyz (рис.
42). Поэтому:
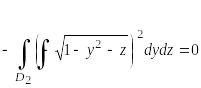
Таким
образом, I1=
.
2.
I2=
т.к.
cosβ=0.
σ03 и σ04 – правая и левая части поверхности σ0, соответствующие y<0 и y>0:
y
=
.
Обе они проектируются на область D3 в плоскости Oxz
(рис. 43); таким образом
I2
=
.
3.
Здесь
,
так как z
0 на 1.
Таким
образом, I=
.
Пример 3. Найти поток вектора
через часть поверхности эллипсоида
,
лежащую в первом октанте, в направлении
внешней нормали.
Решение. Вычислим поверхностный интеграл 2-го рода, сведя его к интегралу 1-го рода:
.
Так как в первом октанте внешняя нормаль эллипсоида со всеми осями координат образует острые углы, то все три направляющих косинуса неотрицательны. Поэтому
(Здесь каждый из интегралов по D1, D2, D3 определяет объем одной восьмой части эллипсоида).
Билет 21. Формула остроградского
Пусть
в пространстве Оxyz
дана трёхмерная область Т, ограниченная
гладкой поверхностью σ, ориентированной
по правилу внешней нормали. Пусть функции
Р(x, y,
z), Q(x,
y, z),
R(x, y,
z) непрерывны вместе
со своими частными производными в
замкнутой области
. Тогда имеет место формула Остроградского,
устанавливающая связь интеграла по
поверхности σ с тройным интегралом по
области Т:
(1)
Пусть
дано векторное поле
= P(M)
+ Q(M)
+ R(M)
,
причём функции P,Q и R имеют частные производные.
Теперь, используя векторное обозначение поверхностного интеграла и понятие дивергенции формула Остроградского может быть записана в виде
=
(2)
(векторная формула записи).
Поток
вектора
через замкнутую поверхность в направлении
внешней нормали равен тройному интегралу
от дивергенции этого вектора, взятому
по области, ограниченной данной
поверхностью.
Пример 1.
Используя теорему Остроградского, найти
поток вектора
через всю поверхность тела
в направлении внешней нормали.
Решение. Имеем
.
Поэтому по формуле (15)
.
Для вычисления
тройного интеграла перейдем к
цилиндрическим координатам:
Уравнение поверхности принимает вид
.
.
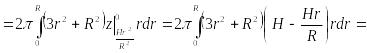
Билет 22. Понятие дифф уравнения, общее решение, задача коши
3.5.1. Понятие дифференциального уравнения
Рассмотрим движение тела массы m в вязкой среде с коэффициентом сопротивления k. По второму закону Ньютона можно записать:
ma = –kv. |
|
Так
как ускорение – первая производная
скорости,
В это уравнение входит неизвестная величина v и ее производная по времени (v c точкой вверху) |
|
|
Уравнения, подобные этому, нередко встречаются в физике, химии, экономике и других дисциплинах. Уравнение вида
|
называется обыкновенным дифференциальным уравнением n-го порядка. Решением этого уравнения является произвольная функция y = y (x), подстановка которой в уравнение превращает его в верное тождество. График решения дифференциального уравнения называется интегральной кривой.
Простейшим дифференциальным уравнением является уравнение вида
|
Чтобы
его решить, нужно представить
производную 
как 
домножить
обе части уравнения на dx и
проинтегрировать обе части получившегося
уравнения:
|
Как видно, это уравнение имеет бесконечное количество решений, отличающихся друг от друга на постоянную C. Выбрать конкретное решение уравнения можно, если знать начальные условия, например, точку, через которую проходит график функции y = y (x). Так, если известно, что
y (x0) = y0, |
то
подставляя это значение в общее
решение 
получаем 
откуда 
и
|
Это
решение можно записать в виде 
.
Общим решением дифференциального уравнения называется функция y = y (x, C1, C2,…, Cn), зависящая от n констант, если она является решением дифференциального уравнения при любых значениях постоянных C1, C2,…, Cn.
Неоднозначность общего решения многих уравнений имеет простой физический смысл. Так, дифференциальное уравнение движения материальной точки массы m под действием силы F (второй закон Ньютона)
|
не определяет однозначно закон движения этой точки: для этого необходимо знать его начальные скорость и координату.
Частным решением дифференциального уравнения называется решение, получаемое из общего решения путем придания определенного значения постоянным Ci.
Задача Коши
Дифференциальное уравнение обычно имеет бесчисленное множество решений. Для того, чтобы из всех решений выделить одно, надо задать какое-либо конкретное значение функции при некотором значении независимого переменного. Задать значение y0 искомой функции при некотором значении x0 независимого переменного — это значит задать начальное условие
= y0.
С геометрической точки зрения задача отыскания решения дифференциального уравнения с заданным начальным условием равносильна тому, чтобы найти ту интегральную кривую, которая проходит через точку M0 (x0, y0) на плоскости XOY.
Естественно возникает вопрос: всегда ли существует решение дифференциального уравнения, удовлетворяющее данному начальному условию, и, если существует, то будет ли оно единственным?
Ответ на поставленные вопросы дает теорема существования и единственности решения дифференциального уравнения первого порядка.
Теорема
Пусть дано уравнение y' = f (x, y) с начальным условием = y0, и относительно функции f (x, y) выполнены следующие условия:
В прямоугольнике R, определенном неравенствами
x0 – a ≤ x ≤ x0 + a,
y0 – b ≤ y ≤ y0 + b,
функция f (x, y) непрерывна. Из этого условия вытекает, что в замкнутой области R функция f (x, y) ограничена, т.е. существует действительное число M > 0 такое, что для любой точки (x, y) ∈ R | f (x,y)| ≤ M.
В области R функция f (x, y) относительно аргумента y удовлетворяет условию Липшица, т.е. существует такое действительное число A > 0, что | f (x, y1) – f (x, y2)| ≤ A|y1 – y2|.
Обозначим
через h меньшее
из двух чисел a, 
.
При данных условиях существует единственное решение y = y(x), где x0 – h ≤ x ≤ x0 + h, удовлетворяющее начальному условию = y0.
Билет 23. Понятие дифа 1го порядка, уравнения с разделяющимися переменными.
Общий вид дифференциального уравнения первого порядка: F (x, y, y ' ) = 0.
Если его возможно разрешить относительно производной y ', то оно приводится к виду y ' = f (x, y). (3.1)
Такая форма дифференциального уравнения первого порядка называется нормальной, а уравнение являетсяразрешимым относительно производной от искомой функции.
Выясним геометрический смысл дифференциального уравнения первого порядка вида (3.1).
Общее решение геометрически задает однопараметрическое семейство интегральных кривых.
Решение y = y (x) уравнения (3.1) представляет собой на плоскости XOY кривую, а y ' — угловой коэффициент касательной к этой кривой в точке M (x, y). Уравнение (3.1) дает, таким образом, соотношение между координатами точки и угловым коэффициентом касательной к интегральной кривой в этой точке.
Задание уравнения (3.1) означает, что в каждой точке M (x, y) области, где определена функция f (x, y), задано направление касательной к интегральной кривой в точке M (x, y). Значит, имея уравнение (3.1) мы получаем поле направлений. Это поле графически можно изобразить, поместив в каждой точке M (x, y) черточку, наклоненную к оси Ox под углом, тангенс которого равен f (x, y).
Задача интегрирования уравнения (3.1) заключается в том, чтобы найти семейство кривых, у которых касательная к каждой точке совпадает с направлением поля в этих точках. Такое истолкование уравнения(3.1) дает графический способ построения его решения.
Уравнения
с разделяющимися переменными могут
быть записаны в виде
,
(1)
а также в виде
.
(2)
Для решения данного уравнения надо обе его части умножить или разделить на такое выражение, чтобы в одну часть уравнения входила только переменная х, а в другую – только у. Затем проинтегрировать обе части, т.е.
для уравнения (1)
для уравнения (2)
.
При делении обеих частей уравнения на выражение, содержащее неизвестные х и у, могут быть потеряны решения, обращающие это выражение в нуль.
Пример
1. Решить уравнение
(3)
Решение. Приводим уравнение к виду (2)
Делим обе части
уравнения на
:
Переменные разделены. Интегрируем обе части уравнения.
.
При делении на , могли быть потеряны решения х = 0 и у = 1. Очевидно, у = 1 – решение уравнения (3), а х =0 – нет.
Интегрирование дифференциального уравнения в общем случае приводит к бесчисленному множеству решений ( отличающимися друг от друга на постоянную величину) .
Чтобы
решение дифференциального уравнения
приобрело конкретный смысл, его надо
подчинить некоторым дополнительным
условиям. Условие, что при
функция
у должна быть равна заданному числу
,
т.е.
,
называется начальным условием. Начальное
условие записывается в виде
или
.
(4)
Задача отыскания решения дифференциального уравнения первого порядка, удовлетворяющего данному начальному условию (4), называется задачей Коши.
Пример 2. Решить задачу Коши
;
у (0)= -1.
Решение. Разделим переменные
;
.
Интегрируем обе части, полученного равенства
;
;
;
-
общее решение данного дифференциального
уравнения. Используя начальное условие
у (0)= -1, определим константу С:
;
;
С=3.
Таким
образом,
-
частное решение дифференциального
уравнения или решение задачи Коши.
Уравнения
вида
приводятся
к уравнениям с разделяющимися переменными
заменой
;
;
т.е.
.
Пример 3.
Решить уравнение
.
Решение.
Сделаем замену
,
тогда
,
т.е.
,
а
,
следовательно,
или
.
Разделяем переменные
.
Интегрируем обе части полученного
равенства
,
,
.
Возвращаясь к переменной у , получаем
.
Это общий интеграл данного дифференциального уравнения.
Билет 24. Однородные уравнеиня 1го порядка
Функция
f(
x,
y)
называется однородной функцией n-го
порядка относительно переменных х и
у , если при любом
справедливо
тождество f(
x,
y)
= 
f(
x,
y).
Например, функция f
( x,
y)=
-
однородная функция первого порядка,
так как f(
x,
y)
=
=
f
( x,
y).
Уравнение
первого порядка
(1)
будет
однородным, если функция f(x,y)
есть однородная функция нулевого порядка
относительно х и у. Это равносильно
тому, что f (x,
y)= f
(1,
),
т.е. функция нулевого порядка зависит
только от отношения аргументов.
Сделаем подстановку
,
т.е. y = zx,
дифференцируя последнее равенство,
найдем
.
Подставляя выражение производной в
уравнение (1), получим
.
Это уравнение с разделяющимися переменными.
Пример
4. Решить уравнение
.
Решение. Справа стоит однородная функция нулевого порядка , следовательно, имеем однородное уравнение. Делаем замену y/x=z, тогда y = zx
,
,
,
Разделяя переменные, получим
;
;
отсюда, интегрируя, находим
или
Подставляя
y/x=z,
получим общий интеграл исходного
уравнения:
