1. Сетевая модель и ее основные элементы. Правила построения сетевых моделей

2. Событие. Временные параметры событий

3. Работа. Временные параметры работ

4. Путь. Характеристики путей. Коэффициент напряженности

5. Оптимизация сетевых графиков по стоимости

6. Оптимизация сетевых графиков по времени

7. Общая постановка задачи линейного программирования. Формы ее записи

8. Геометрическая интерпретация задачи линейного программирования

9. Симпл метод реш задачи лин программирования. Алгоритм построения начального опорного плана

10. Симпл метод реш задачи линейного программирования. Алгоритм построения оптимального плана

11. Понятие двойственности. Правила построения двойственных задач

12. Экономическая интерпретация задачи, двойственной задаче об использовании ресурсов

13. Теоремы двойственности – формулировка, экономический смысл

14. Проверка решения задачи линейного программирования на устойчивость. Изменение вектора цен.

15. Проверка реш задачи лин прогр на устойчивость. Изменение вектора ограничений по ресурсам

16. Экономико-математическая модель транспортной задачи. Построение исходного базисного плана

17. Транспортная задача. Построение оптимального плана

18. Транспортная задача в сетевой форме. Метод решения.

19. Венгерский алгоритм решения задачи о назначениях.

20. Эконометрика и ее связь с другими дисциплинами

21. Эконометрическая модель и основные типы данных

22. Эндогенные и экзогенные переменные. Цель эконометрического моделирования. Типы связей

23. Классификация и основные типы эконометрических моделей

24. Этапы построения эконометрических моделей

25. Случайная величина. Типы и описание случайных величин.

26. Основные числовые характеристики случайных величин

27. Регрессионный анализ. Статистическая постановка задачи

28. Модель парной линейной регрессии. МНК

29. Проверка гипотез отн-но коэффициентов уравнения парной регрессии. Доверительные интервалы

30. Проверка общего качества уравнения парной регрессии. Коэффициент детерминации

31. Множественная линейная регрессия. Определение параметров уравнения регрессии

32. Проверка стат-ой значимости коэф-ов ур-ия множ-ой линейной регрессии и их интервальные оценки

33. Проверка общего качества уравнения множественной регрессии

34. Проверка гипотезы об общей значимости множественной линейной регрессии

35. Анализ статистической значимости коэффициента детерминации

36. Модели управления запасами. Основные понятия

37. Статическая детерминированная модель управления запасами без дефицита

38. Статическая детерминированная модель управления запасами с дефицитом

39. Предпочтения потребителей. Функция полезности

40. Модель поведения потребителя

41. Взаимозаменяемость благ. Эффекты компенсации. Уравнение Слуцкого

42. Игровые модели исследования операций

43. Матричные игры и понятие седловой точки

44. Решение игр в смешанных стратегиях. Приведение матричной игры к задаче линейного прогр

45. Игры с природой или принятие решений в условиях неопределённости и риска

46. Постановка задачи динамического программирования

47. Принцип оптимальности и уравнения Беллмана

1-4. Сетевая модель и её основные элементы. Правила построения сетевых моделей

Сетевой моделью (СМ) называется экономико-математическая модель, отражающая весь комплекс работ и событий, связанных с реализацией проекта в их логической и технологической последовательности и связи.

Математическим аппаратом СМ является теория графов.

Графом называется совокупность двух конечных множеств: множества точек (х1,х2,…, xn), которые называются вершинами, и множества пар вершин, которые называются ребрами (e1,e2,…,en). Если пары вершин упорядочены, т.е. на каждом ребре задано направление, ребро называется дугой, а граф называется ориентированным; иначе – неориентированным.

Последовательность ребер, ведущая от некоторой вершины к другой образует путь. Замкнутый путь называется циклом.

Граф называется связным, если для любых двух вершин существует путь, их соединяющий. В противном случае граф называется несвязным.

Если дугам присвоены некоторые числа или веса (C_ij), то граф называется нагруженным.

В ориентированном графе вершины, не имеющие входных дуг, называются начальными (источниками), а вершины не имеющие выходных дуг – конечными (стоками), остальные – промежуточными.

Основные понятия СМ: событие, работа, путь.Работа характеризует любое действие, требующее затрат времени или ресурсов. Работами считаются и процессы, не требующие затрат времени и ресурсов и устанавливающие зависимости выполнения работ, такие работы называются фиктивными.Работа обозначается парой чисел (i, j), где i – номер события, из которого работа выходит, j –номер события, в которое она входит. Работа не может начаться раньше, чем свершится событие, из которого она выходит. Каждая работа имеет свою продолжительность t(i,j). Работы на графах обозначаются дугами (стрелками), фиктивные работы обозначаются пунктирными стрелками. Событиями называются начало или завершение одной или нескольких работ. Они не имеют протяженности во времени. Событие совершается в тот момент, когда оканчивается последняя работа, входящая в него. На графе события изображаются кружками, внутри которых записывается номер события. В моделях СПУ имеется одно начальное событие (номер 0), одно конечное событие (номер N) и промежуточные события (номер i).

Путь – цепочка следующих друг за другом работ (дуг), соединяющих начальную и конечную его вершины. Полный путь L – путь, начало которого совпадает с начальным событием сети, а конец – с завершающим.Продолжительность пути определяется суммой продолжительностей составляющих его работ. Путь, имеющий максимальную продолжительность, называют критическим (L_кр), а его продолжительность – t_кр. Работы, принадлежащие критическому пути, называются критическими. Их несвоевременное выполнение ведет к срыву сроков всего комплекса работ. Таким образом, в СМ работы представляются дугами, а события – вершинами графа, отображая весь процесс выполнения комплекса работ. Сетевая модель должна удовлетворяет следующим требованиям:

1. Не должно быть событий с одинаковыми номерами.

2. Для каждой работы (i,j) i<j.

3. Должны быть только одно начальное и одно конечное события.

4. Отсутствуют циклы, т.е. замкнутые пути, соединяющие событие с ним же самим.

При выполнении этих требований можно приступать к вычислениям числовых характеристик СМ. Исходные числовые данные СМ представляются в виде таблицы длительности выполнения каждой работы.

Характеристики путей

1.Продолжительность пути, равна сумме продолжительностей составляющих ее работ.

2. Резерв времени пути – разность между длинами критического пути и рассматриваемого пути.

Резерв времени пути показывает, на сколько может увеличиться продолжительность работ, составляющих данный путь, без изменения продолжительности срока выполнения всех работ. Критический путь и его длина. Критический путь L_кр состоит из работ (i,j), у которых полный резерв времени равен нулю R_п(i,j)=0, кроме этого резерв времени всех событий i на критическом пути R(i) =0.

L_кр определяет величину наиболее длинного пути, от начального до конечного события сети. Длина критический пути равна

t_кр=t_p(N)= t_п(N). В проекте может быть несколько критических путей.

1-4. временные параметры сетевых графиков

Ранний срок свершения события: t_p(0) = 0,

t_p(j) = max_i {t_p(i) + t(ij)}, j = 1/N, характеризует самый ранний срок завершения всех путей в него входящих. Этот показатель определяется, начиная с начального события сети.

Поздний срок свершения события: t_п(N) = t_p(N),

t_п(i) = min_j {t_п(j) - t(ij) }, i = 1/N-1, характеризует самый поздний срок, после которого остается ровно столько времени, сколько требуется для завершения всех путей следующих за этим событием.

Для каждого события определяется резерв времени:

R(i) = t_п(i) - t_p(i). Резерв показывает, на какой максимальный срок можно задержать наступление этого события, не вызывая при этом увеличения срока выполнения всего комплекса работ. Резервы времени для событий на критическом пути равны нулю, R(i)=0.

Характеристики работ (i,j):

Ранний срок начала работы: t_pн(i,j)=t_p(i).

Ранний срок окончания работы: t_po(i,j)= t_pн(i,j) + t_ij =t_p(i) + t_ij

Поздний срок начала работы: t_пн(i,j)=t_п(j) – t_ij.

Поздний срок окончания работы: t_по(i,j) = t_п(j).

Полный резерв R_п(i,j) = t_п(j) - t_p(i) - t_ij. Это максимальный запас времени, на который можно отсрочить начало или увеличить длительность работы без увеличения длительности критического пути. Работы на критическом пути не имеют полного резерва времени, для них R_п(i,j)=0.

Частный резерв R₁(i,j) = R_п(i,j) - R(i) = t_п(j) – t_п(i) - t_ij. Это часть полного резерва, на которую можно увеличить продолжительность работы, не изменив позднего срока ее начального события.

Свободный резерв R_с(i,j) = R_п(i,j) - R(j) = t_p(j) – t_p(i) - t_ij. Это максимальный запас времени, на который можно задержать начало работы или (если она началась в ранний срок) увеличит ее продолжительность, не изменяя ранних сроков начала последующих работ.

Независимый резерв R_н(i,j) = R_п(i,j) - R(i) – R(j) = t_p(j) – t_п(i) - t_ij. Запас времени, при котором все предшествующие работы заканчиваются в поздние сроки, а все последующие – начинаются в ранние сроки. Использование этого резерва не влияет на величину резервов времени других работ.

Если на L_кр лежит начальное событие i работы (i,j), то R_п(i,j) = R₁(i,j)

Если на L_кр лежит конечное событие j работы (i,j), то R_п(i,j) = R_c(i,j)

Если на L_кр лежат и событие i, и событие j работы (i,j), а сама работа не принадлежит критическому пути, то R_п(i,j) = R_с(i,j) = R_н(i,j).

Работы, лежащие на критическом пути резервов времени не имеют. Для оценки трудности своевременного выполнения работ служит коэффициент напряженности работ: К_н(i,j) = ( t(L_max)-t_кр ) / (t_кр-t^'_кр) = 1 – R_п(i,j) / (t_кр-t^'_кр),

где: t(L_max) – продолжительность максимального пути, проходящего через работу (i,j);

t^'_кр – продолжительность отрезка рассматриваемого пути, совпадающего с критическим путем.

Видно, что К_н(i,j)<1. Чем ближе К_н(i,j) к 1, тем сложнее выполнить данную работу в установленный срок. Напряженность критических работ полагается равной 1.

Все работы СМ могут быть разделены на 3 группы: напряженные – К_н(i,j)>0,8; подкритические – 0,6< К_н(i,j) <0,8; резервные – К_н(i,j)<0,6.

??. Задача минимизации стоимости проектов

Задача минимизации стоимости проекта. Минимизация стоимости проекта при сохранении t_kp достигается увеличением продолжительности выполнения некритических работ, использованием их свободных резервов времени, которые не влияют на ранние сроки начала последующих работ.

Увеличения продолжительности осуществляется на величину , пока не будет исчерпан весь свободный резерв времени, или не будет достигнуто максимально допустимое значение продолжительности работы в (i,j), т.е.:

(5.5)

Тогда полная стоимость проекта

С=∑ С(i,j),

? Задача минимизации времени выполнения проекта

Она возможна за счет сокращения продолжительности работ лежащих на Крит пути. С этой целью проводится расчет исходного сетевого графика и выполняется его оптимизация t(ij)=b(ij)

Алгоритм:

1. составляем список всех полных путей и определяем их длительность

2. начиная с Крит пути, если он один строится линейные графы всех полных путей с упорядочиванием по уменьшению их длительности

3. на каждом шаге начинается с первого к=1, составляется список {L^k_kp} критических путей рассчитыв продолжительность и его стоимость. Если t(ij)=a(ij), то расчеты окончены.

4. Для путей {L^k_kp} из списка критических путей, определ работы подлежащие содержанию:

   • {L^k_kp} есть работы общие для всех путей, выбирается одна общая работа (p, q) для которой h^*_pq=min h(ij), t(ij)>a(ij)

Определяется время сокращения длительности выбранной работы

T= min {t^/(p,q) – a(p,q)

Сокращение длительности работы не превышает длительность ближайшего к Крит пути

Tⁿ_(p,q)= t_(p,q)- t

C учетом изменения времени выполнения работ идет пересчет длин всех полных путей.

C(t)=c+ h_pq)(T_kp-t)

Если новая продолжительность работы tⁿ_(pq)=a(pq), то она в величинах не участвует т к исчерпала свой резерв времени

5. с=c(t) строится график зависимости стоимости от длины критического пути

6. для определения миним времени t^* по заданной стоимости проекта С*, решается уравнение C(t^n)=C

^{Замечание:} Дополнительные затраты связанные с сокращением t1-t2 определяется разностью C(t2)-C(t1)

5-6 Задача оптимизации моделей СПУ

Общие сведения Сокращение времени завершения проекта, как правило, связано с привлечением дополнительных средств (количество рабочих, сверхурочные работы). Постановка задачи 1. Для сокращения времени выполнения проекта выделяется некоторая сумма дополнительных средств В. Задан сетевой график G=(Е,U) выполнения проекта, где Е - множество событий, U - множество работ. Продолжительность каждой работы равна t_ij . Известно, что вложение дополнительных средств х_ij в работу (ij) сокращает время ее выполнения от t до t'ij,. Для каждой работы существует минимально возможное время ее выполнения d_ij.

Требуется определить время начала tⁿ_ij и окончания t⁰_ij выполнения работ, а также количество дополнительных средств х_ij, которые необходимо вложить в работы (і, Д чтобы общее время выполнения проекта было минимальным, а сумма вложенных дополнительных средств не превышала величины В, время выполнения каждой работы было не меньше минимально возможного времени.

Математически условия задачи можно записать

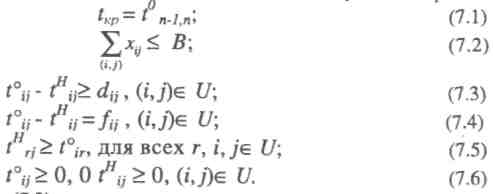
Ограничение (7.2) определяет сумму вложенных дополнительных средств: она не должна превышать величины В. Ограничения (7.3) показывают, что продолжительность каждой работы должна быть не менее минимально возможной ее продолжительности. Ограничения-равенства (7.4) показывают зависимость продолжительности каждой работы от вложенных в нее дополнительных средств. Ограничения (7.5) обеспечивают выполнение условий предшествования работ в соответствии с топологией сети: время начала выполнения каждой работы должно быть не меньше времени окончания непосредственно предшествующих ей работ. Ограничение (7.6) - условие неотрицательности.

Если в последнее событие сети п входят сразу несколько работ, то необходимо добавить фиктивную работу (n, п + 1), время выполнения которой равно нулю (t⁰_nij+1 – tⁿ_nn+1- = 0) добавить в ограничение (7.4). Тогда целевая функция запишется так : t_кр= t⁰_n-1,n(min).

Постановка задачи 2. Пусть задан срок выполнения проекта t₀, а расчетное время t_кр>=t₀. В этом случае оптимизация комплекса работ сводится к сокращению продолжительности критического пути. Задача заключается в определении величины дополнительных вложений x_ij в отдельные работы проекта с тем, чтобы общий срок его выполнения не превышал заданной величины t₀ , а суммарный расход дополнительных средств был минимальным. Время выполнения каждой работы должно быть не меньше минимально возможного времени d_ij.

Математическая запись этой задачи имеет вид

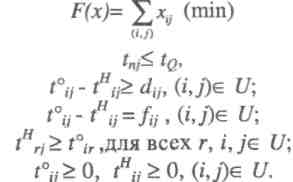
Смысл ограничений аналогичен. Приведенные постановки задачи относятся к классу задач математического программирования и могут быть решены известными методами в зависимости от вида функций f_ij (х_ij). Если предположить, что продолжительность выполнения работ линейно зависит от дополнительно вложенных средств и выражается соотношением (t'_ij =t_ij – к_ij Х_ij , где к_ij -технологические коэффициенты использования дополнительных средств, го будем иметь задачу линейного программирования