
Часть 3. Ряды.
Задача
1. Найти
сумму ряда:
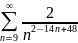
Произведем эквивалентные преобразования ряда:
Так
как
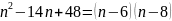 ,
то получаем, что исходный ряд мы можем
переписать в следующем виде:
,
то получаем, что исходный ряд мы можем
переписать в следующем виде:
=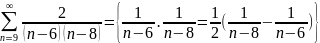 =
=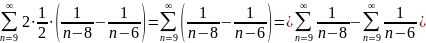 .
.
Рассмотрим
ряд
 .
.
Произведем
замену
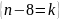 ,
тогда суммирование будет производиться
от k=n-8=
,
тогда суммирование будет производиться
от k=n-8= =9-8=1,
a
=9-8=1,
a
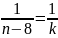 .
.
Подставим
полученные значения в ряд


Произведем
аналогичные преобразования и с рядом
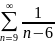 .
Тогда для него замена
.
Тогда для него замена
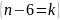 :
:
начальное
k=n-6=
=9-6=3,
a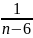 =
=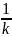 .
.
Подставим
данные в
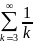 .Итак,
мы получили, что исходный ряд равен
разности двух рядов:
.Итак,
мы получили, что исходный ряд равен
разности двух рядов:
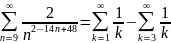 =
=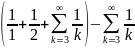 =
=
Ответ: =
Задача 2. Исследовать ряд на сходимость:
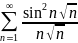
Обозначим

Тогда
для всех n
верно следующее утверждение: ,
так как
,
так как
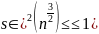
Докажем
сходимость ряда
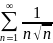 .
Тогда из его сходимости будет следовать
сходимость исходного ряда, так как тогда
он будет ограничен сходящихся рядом
сверху и нулем снизу(все члены ряда
неотрицательны).
.
Тогда из его сходимости будет следовать
сходимость исходного ряда, так как тогда
он будет ограничен сходящихся рядом
сверху и нулем снизу(все члены ряда
неотрицательны).
Обозначим
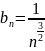 .
По признаку сравнения (говорящему, что
ряд вида
.
По признаку сравнения (говорящему, что
ряд вида
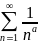 сходится только при условии, что а строго
больше 1, т.е. а
сходится только при условии, что а строго
больше 1, т.е. а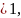 и расходится в противном случае, при
а
и расходится в противном случае, при
а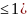 ,
ряд
сходится, так как выполняется условие
сходимости:1.5
,
ряд
сходится, так как выполняется условие
сходимости:1.5 .
.
Поэтому и исходный тоже сходится.
Ответ: ряд сходится.
Задача 3. Исследовать ряд на сходимость:
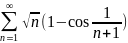
Обозначим
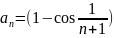
При
n
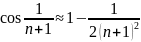 ,поэтому сходимость исходного ряда
эквивалентна сходимости следующего
ряда:
,поэтому сходимость исходного ряда
эквивалентна сходимости следующего
ряда:
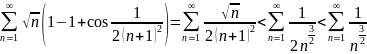
Докажем
сходимость ряда
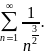 Тогда из его сходимости будет следовать
сходимость исходного ряда, так как тогда
он будет ограничен сходящимся рядом
сверху и нулем снизу ( все члены ряда
неотрицательны).
Тогда из его сходимости будет следовать
сходимость исходного ряда, так как тогда
он будет ограничен сходящимся рядом
сверху и нулем снизу ( все члены ряда
неотрицательны).
Обозначим
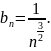 По признаку сравнения (говорящему, что
ряд вида
сходится только при условии, что а
строго больше 1, т.е. а
и расходится в противном случае, при а
ряд
По признаку сравнения (говорящему, что
ряд вида
сходится только при условии, что а
строго больше 1, т.е. а
и расходится в противном случае, при а
ряд
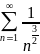 сходится, так как выполняется условие
сходимости: 1,5
сходится, так как выполняется условие
сходимости: 1,5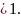
Поэтому и исходный ряд тоже сходится.
Ответ:
ряд сходится.
Задача
4. Исследовать
ряд на сходимость:

Обозначим
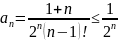 ,
т.к.
,
т.к.
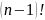 растет быстрее чем (n+1)
при n
.
растет быстрее чем (n+1)
при n
.
Докажем
сходимость ряда
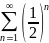 .
Тогда из его сходимости будет следовать
сходимость исходного ряда, т.к. тогда
он будет ограничен сходящимся рядом
сверху и нулем снизу ( все члены ряда
неотрицательны).
.
Тогда из его сходимости будет следовать
сходимость исходного ряда, т.к. тогда
он будет ограничен сходящимся рядом
сверху и нулем снизу ( все члены ряда
неотрицательны).
есть
сумма бесконечной убывающей геометрической
прогрессии, которая находится по формуле
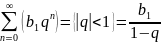
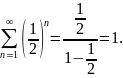
Тогда исходный ряд тоже сходится.
Ответ: сходится.
Задача
5. Исследовать
ряд на сходимость:
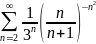
Воспользуемся признаком Коши:
Если
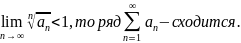
Если
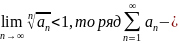 расходится.
расходится.
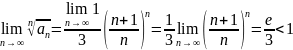
Таким образом, по признаку Коши исходный ряд является сходящимся.
Ответ: сходится.
Задача
6. Исследовать
ряд на сходимость:
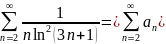
Воспользуемся предельным признаком сходимости.
Если
два ряда
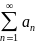 и
и
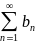 удовлетворяют условию:
удовлетворяют условию:
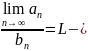 конечное число, не равное 0, то ряды
и
конечное число, не равное 0, то ряды
и
Сходится или расходятся одновременно.
Рассмотрим следующий ряд:
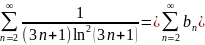
lim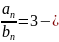 это
конечное число число, не равное 0
это
конечное число число, не равное 0
Значит,
ряды
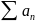 и
и
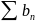 сходится
или расходится одновременно.
сходится
или расходится одновременно.
Для исследования сходимости второго ряда воспользуемся интегральным признаком сходимости рядов.
Если
некоторая функция f(x)
удовлетворяет условию f(n)=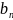 ,
то если
,
то если
 сходится, то и ряд
сходится, то и ряд
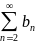 сходится, а если
расходится, то и ряд
расходится.
сходится, а если
расходится, то и ряд
расходится.
Рассмотрим следующую функцию:
f(x)=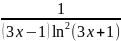
Если сходится, то и ряд сходится, если интеграл расходится, то и ряд расходится.
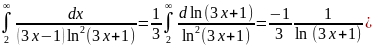
Интеграл сходится, значит и ряд сходится. Из сходимости этого ряда
следует сходимости исходного.
Ответ: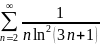 сходится.
сходится.
Задача 7.
Исследовать
ряд на сходимость:
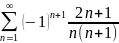
Воспользуемся признаками Лейбница:
если
ряд
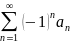 удовлетворяет условиям:
удовлетворяет условиям:
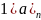 -
монотонно убывающая, начиная с некоторого
n=N
-
монотонно убывающая, начиная с некоторого
n=N
