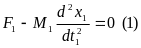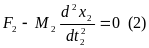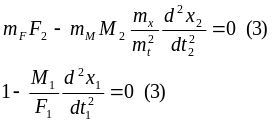Не знПонятие модели. Понятие моделирования. Типы моделирования.

Требования, предъявляемые к моделям. Математическое моделирование. Классификация математических моделей.

Моделирование – представление характеристик поведения физической или абстрактной системы (оригинала) с помощью другой системы (модели).

Моделирование – выявление свойств каких-либо объектов, систем или процессов путем построения и исследования их моделей.

Модель – материальный, мысленно представляемый объект, который в процессе познания замещает объект оригинал, сохраняя некоторые важные для данного исследования типичные его черты.

Модель – материальный объект, система математических зависимостей или программа, имитирующие структуру или функционирование исследуемого объекта.

Модель – система или процесс, свойства которых в каком-либо смысле подобны свойствам другой системы или процесса.

Из этих определений следует, что модель – отображение натуры. Она всегда проще оригинала. Причем для одного и того же оригинала может быть построено множество моделей.

Все существующие виды моделирования можно объединить в две большие группы:

Виды моделирования
Материальные (предметы)	Идеальные (абстрактные)
Физические	Интуитивное
Аналоговые	Знаковое
	Математическое

К материальным относят моделирование, при котором модели воспроизводят основные геометрические, физические, динамические и функциональные характеристики оригинала.

В основе материального моделирования лежит понятие подобия прямого, косвенного и условного.

Прямое подобие устанавливается через физическое взаимодействие и приводит к физической модели.

Косвенное подобие устанавливается через общую абстрактную модель и приводит к аналоговой модели.

Условное подобие устанавливается через соглашение.

Примерами могут служить: удостоверение личности, чертежи, схемы, сигналы.

Физическим называют моделирование, при котором оригиналу соответствует его увеличенная или уменьшенная копия.

Теоретической основой является теория подобия.

Аналоговое моделирование основано на одинаковом формальном описании различных физических процессов.

Интуитивное моделирование основано на не поддающемся формализации представлении человека о тех или иных объектах процесса. Весь жизненный опыт человека – это его интуитивная модель окружающего мира.

Важнейшим видом является знаковое моделирование, где в качестве моделей используются совокупности знаков и правила их преобразования.

Одним из видов знакового моделирования является математическая, поскольку в математике обеспечена высочайшая степень формализации знаковых преобразований.

Требования к моделям.

1. степень универсальности характеризует полноту отображения свойств реального объекта. Полной универсальностью обладает только оригинал;

2. точность оценивается степенью совпадения параметров оригинала и соответствующих параметров модели, полученных в ходе моделирования;

3. адекватность – способность отображать исследуемые свойства объекта с заданной точностью в указанной области изменения параметров.

4. экономичность характеризует материальные (финансовые, трудовые, временные) и вычислительные (требуемый объем памяти, требуемое машинное время) затраты на реализацию модели.

5. ингерентность, т.е. степень согласованности с общим уровнем развития техники технологий культуры.

Математическое моделирование – это процесс установления соответствия данного реального объекта, этот объект описывается с помощью математической логики, мат.методов и носит чисто теоретический характер

Математическая модель – совокупность мат.объектов(чисел, переменных) и отношения между ними, которая адекватно отображает св-во исследуемого объекта.

Существует достаточно большое число классификационных признаков моделей. Прежде всего, модели можно разделить на позна­вательные и прагматические.

Познавательные модели являются формой организации и пред­ставления знаний, средством соединения новых знаний с имеющими­ся; они отражают реальность и поэтому "подгоняются" под неё.

Прагматические модели являются средством управления, сред­ством организаций практических действий, способом представления образцово правильных действий или их результата, т.е. рабочим пред­ставлением целей; они отражают не существующее на данный момент, но желаемое и (возможно) осуществимое, поэтому реальность "подго­няется" под модель.

Ниже представлен один из возможных способов классификации моделей по наиболее существенным признакам.

A. По области применения: модели технических, экономиче­ских, биологических, социальных и др. объектов и систем.

B. В зависимости от класса решаемых задач различают деск­риптивные (описательные), оптимизационные, поведенческие (имита­ционные), информационные и т.п. модели.

C. По характеру отображаемых свойств: структурные и функ­циональные модели.

С.1. Структурные модели подразделяются на топологические и геометрические.

С. 1.1, В топологических моделях отображаются состав и взаи­мосвязи элементов системы. Их чаще всего применяют для решения задач привязки конструктивных элементов к определенным простран­ственным позициям (например, задача компоновки оборудования, за­дача трассировки соединений в печатных платах) или к относительным моментам времени (например, задача разработки расписаний, задача формирования маршрутов технологических процессов). Топо­логические модели обычно имеют форму графов, таблиц (матриц), списков и т.п.

С. 1.2. В геометрических моделях дополнительно к сведениям о взаимном расположении элементов содержатся сведения о форме де­талей. Их чаще всего применяют для решения задач конструирования в машиностроении, приборостроении, радиоэлектронике, для оформления конструкторской документации, при задании исходных данных на разработку технологических процессов изготовления деталей. Гео­метрические модели обычно имеют форму уравнений линий и поверхностей (аналитические модели), графов и списков, отображающих конструкции из типовых элементов, и т.п. В машиностроении для ото­бражения геометрических свойств деталей со сложными поверхностя­ми используют каркасные модели в виде множества точек или линий, принадлежащих моделируемой поверхности. В частности, на поверх­ность может быть нанесена прямоугольная сетка.

С.2. Функциональные модели предназначены для отображения физических (электрических, механических,, гидравлических, тепловых, оптических) или информационных процессов, протекающих при функционировании или изготовлении объектам Обычно функциональ­ные модели представляют собой системы уравнений, связывающих внутренние, внешние и выходные параметры объекта.

Параметр объекта - величина, характеризующая некоторое свойство объекта или режим его функционирования, Выходные па­раметры - показатели качества, по которым можно судить о правиль­ности функционирования объекта, т.е. они характеризуют свойства системы. Внутренние параметры характеризуют свойства элементов системы, а внешние - свойства внешней (по отношению к системе) среды. Например, для электронного усилителя? выходными парамет­рами являются полоса пропускания, коэффициент усиления на сред­них частотах, входное сопротивление, мощность рассеяния; внутрен­ние параметры - R, L, С, VD, VT и т.д.; внешние параметры - сопро­тивление нагрузки, напряжение питания и т.д.

С.2.1. Статические функциональные модели описываются сис­темами линейных или нелинейных алгебраичееких уравнений (СЛАУ, СНАУ) и предназначены для исследования установившихся состояний объекта.

С.2.2. Динамические функциональные модели описываются системами обыкновенных дифференциальных уравнений (ОДУ) или дифференциальных уравнений в частных производных (ДУЧП), что позволяет анализировать переходные процессы в объекте.

По способу представления свойств объекта различают анали­тические и алгоритмические функциональные модели.

С.2.3. Аналитические модели представляют собой явные выра­жения выходных параметров как функций входных и внутренних па­раметров. Они характеризуются высокой экономичностью, однако их удается получить, как правило, лишь при принятии существенных допущений и ограничений, снижающих точность и сужающих область адекватности модели.

С.2.4. Алгоритмические модели выражают связи выходных па­раметров с внутренними и внешними параметрами объекта в форме того или иного алгоритма (программы).

Имитационная модель - алгоритмическая модель, отражающая поведение исследуемого объекта (системы) во времени при задании тех или иных внешних воздействий.

D. В зависимости от места в иерархии описаний различают мо­дели микро-, макро- и мета- уровней.

D.I. Особенностью моделей микроуровня является отражение физических процессов, протекающих в

непрерывных пространстве и времени (НПНВ - модели). Типичная форма этих моделей - системы ДУЧП, в которых независимыми переменными являются пространст­венные координаты х, у, z и время t С помощью этих моделей рас­считываются поля механических напряжений и деформаций, электри­ческих потенциалов, давлений, температур и т.д.

D.2. На макроуровне используют укрупненную дискретизацию пространства или времени, что позволяет перейти к системам ОДУ (ДПНВ-, НПДВ- модели) или к СЛАУ (ДПДВ- модели). Системы ОДУ являются универсальной формой представления моделей, т.к. позво­ляют анализировать динамические процессы и установившиеся со­стояния объектов.

D.3. На метауровне в качестве элементов системы принимают достаточно сложные совокупности ее компонентов (например, пред­приятие или отрасль в целом). Важный класс моделей этого уровня составляют модели массового обслуживания, которые применяются для описания процессов функционирования информационных и вы­числительных систем, производственных участков, линий и цехов.

Приведенная выше классификация, естественно, не претендует на полноту и единственность подхода и отражает лишь взгляд авторов на эту проблему.

Физическое моделирование. Понятие подобия. Критерии подобия. Первая теорема подобия. Зависимые и независимые единицы измерения. Нахождение числа критериев подобия. Вторая теорема подобия. Третья теорема подобия.

В основе физического моделирования лежит прямое подобие, поэтому, прежде всего, нужно уточнить понятие подобия. Элементарное понятие подобия вводится в планиметрии:

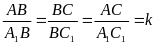
В общем случае имеем следующий случай: пусть имеется некоторый оригинал, описываемый как некая ф-ция от некоторого набора параметров 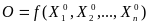, и пусть имеется модель, описываемая как . Если для всех параметров x_i выполняются соотношения 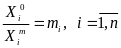, то говорят, что объект и модель подобны. Это означает, что, исследуя свойства модели, можно перенести полученные результаты на объект, пересчитав все параметры с помощью масштабов m_i.

Проблема заключается в том, что не все m_i могут принимать независимые значения, поскольку среди параметров X есть взаимосвязанные, например, физическими законами. Простейший случай I=U/R, тогда m_i=m_U/m_R. Поэтому из трех величин произвольно могут быть выбраны только две.

Правило выбора масштабных соотношений определяет теория подобия, в основе которой лежат три теоремы.

Тогда под подобием понимают такое взаимооднозначное соот­ветствие между параметрами модели и объекта, при котором правила перехода (критерии подобия) от X i_м к X i₀ известны.

Теория подобия дает возможность установить наличие подобия и разработать способы его достижения. Основу теории подобия со­ставляют три теоремы, которые ниже рассмотрены на примерах.

Первая теорема подобия (теорема Ньютона-Бертрана): подобные явления имеют определенные сочетания параметров, называемые критериями подобия (π), численно одинаковые.

Проиллюстрируем примеры следующими примерами: пусть имеем механические поступательные системы, подчиняющиеся второму закону Ньютона:

Согласно второму закону Ньютона они описываются уравнениями вида:

F1-M1a1=0

F2-M2a2=0

M₁=m_M·M₂; x₁=m_x·x₂; t₁=m_t·t₂ – тогда уравнения примут следующий вид:

Произвольно введем масштабные коэффициенты:

M1=mM·M2 F1=mF·F2

x1=mx·x2 t1=m1·t2

Подставляя полученные соотношения в уравнение (3), имеем:

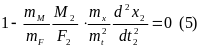
Сравнивая (4) и (5), приходим к фундаментальному соотношению для механических поступательных систем: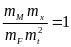

Переходя от масштаба к соответствующим физическим величинам, получаем формулировку критерия подобия Ньютона: 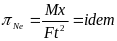. Оно справедливо для всех подобных механических поступательных систем. - величина обязательно безразмерная.

Полученный результат трактуется следующим образом: для всех механических поступательных систем, подчиняющихся второму закону Ньютона, величина π_Ne (безразмерная!) должна быть одной и той же, если эти системы подобны.

Следствие: количество критериев подобия всегда на единицу меньше числа членов уравнения, описывающего исследуемый процесс.

Критерий Ньютона является динамическим, поскольку в него входит время.

Кроме динамических существует статистические критерии, например: для электрических цепей, подчиняющихся закону Ома, имеем: .

Теорема вводит понятие критерия подобия, но не дает формальные процедуры его определения.

Вторая теорема подобия: всякое полное уравнение физического процесса, записанное в определенной системе единиц измерения, может быть представлено функциональной зависимостью критериев подобия.

Полным уравнением будем называть уравнение, в которое входят все интересующие нас в данном случае физические величины.

Системой единиц измерения называется совокупность определенным образом установленных единиц измерения, физических величин, которая включает основные (первичные), производные (вторичные) и дополнительные единицы измерения.

Основные единицы измерения выбираются произвольно!

Г ОСТ 8.417-81 называется «Единицы физических величин», определяет систему СИ, в которой введено семь основных единиц:

- длина, L. м;

- масса, M, кг;

- время, T, с;

- сила электрического тока, I, А;

- термодинамическая температура, Θ, К;

- количество вещества, N, моль;

- сила света, J, кд.

Д ополнительными единицами являются радиан и стерадиан.

Производные единицы измерения выражаются через основные с помощью формул размерности, которые отражают те или иные физические законы, например: из второго закона Ньютона следует формула размерности вида f=ma; [f]=[M]¹[L]¹[T]^-2=кг·м·с^-2=Н.

Аналогично устанавливаются единицы измерения для электрических величин:

- потенциал, разность потенциалов, напряжение, Вольт [B]=[L]²[M]¹[T]^-3[I]^-1;

- емкость, Фарада [Ф]=[L]^-2[M]^-1[T]⁴[I]²;

- сопротивление, Ом [Ом]=[L]²[M]¹[T]^-3[I]^-2;

- индуктивность, Генри [Гн]=[L]²[M]¹[T]^-2[I]^-2.

П оказатели степеней при основных единицах измерения образуют матрицы размерности.

Группой независимых параметров объекта (процесса) называется такая группа, в которой размерность ни одного параметра не может быть получена из размерностей других параметров. Например, параметры m (масса), x (перемещение), υ (скорость) образуют группу независимых параметров, а группа m, f, a является группой зависимых параметров →f-ma=0.

Тогда некий объект (процесс) можно описать функциональной зависимостью бита O=f(x₁,x₂,…,x_k,x_k+1,…,x_m), где x₁,…,x_k – независимые параметры, а x_k+1,…,x_m – зависимые. Тогда количество критериев подобия будет равно m-k, т.е. будем иметь π₁,π₂,…, π_m-k, а k=rankA, A – матрица, образованная в формулу размерности для параметров x₁,x_m. Рангом матрицы называется наибольший порядок определителя отличного от нуля.

В результате , где α_i – целочисленная степень.

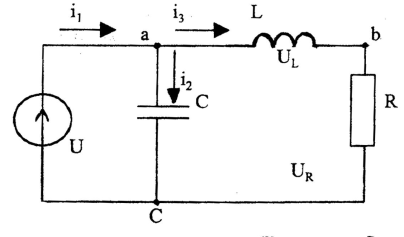
Рассмотрим пример: пусть есть электрическая цепь, изображенная на рисунке:

Эта цепь описывается уравнением вида: iR+Ldi/dt-U=0.

Рассуждая также как при выводе критерия Ньютона, имеем:

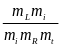
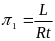
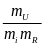
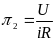
В соответствии со второй теоремой подобия, прежде всего, составляем полное уравнение физического процесса: 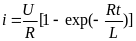. Имеем пять параметров: m=5 i, U, R, L, t. Формируем матрицу A следующим образом:

X	L	M	T	I
i	0	0	0	1
U	2	1	-3	-1
R	2	1	-3	-2
L	2	1	-2	-2
t	0	0	1	0

rankA=3

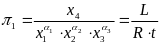
Критерии определяются следующим образом: разделим параметр на группы независимых и зависимых. Независимыми являются i,R,T; зависимыми являются L,U. Тогда в конечном итоге имее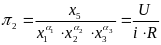м: . Причем ,

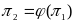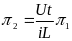
В результате формальная запись теоремы принимает вид: O=f(1,1,1,π₁,π₂).

Итог: таким образом, первая теорема вводит само понятие критерия подобия как безмерной величины, связывающих физические параметры объекта или процесса. Вторая теорема дает формальную процедуру для определения количества и конкретного вида критериев подобия, используя понятие формулы размерности.

Третья теорема подобия (теорема Кирпичева-Гухмана): необходимым и достаточным условиями для создания подобия явля­ются: а) пропорциональность сходственных параметров, входящих в условия однозначности; б) равенство критериев подобия сопостав­ляемых явлений (процессов).

Для примера рассмотрим электрическую схему из последова­тельно соединенных источника э.д.с. U, ключа Кл, емкости С, индуктивности L и сопротивления R (рис. 2.4).

Процессы в схеме описываются уравнением вида

В данном случае имеем m = 6 физических величин (парамет­ров):

Из второй теоремы подобия следует, что к = 3, т.е. число критериев подобия m-k = 3. При выборе группы независи­мых параметров

получаем

Тогда для двух произвольных систем такой структуры справед­ливы соотношения вида:

из которых следуют выражения для определения масштабов:

Для независимых переменных U, С, t соответствующие мас­штабы выбираем произвольно.

Тогда для зависимых переменных L, R, i масштабы вычисляются из В результа­те получаем

Аналоговое моделирование. Терминология. Последовательность действий при моделировании. Положения, используемые при переходе от одной системы к другой.

Большинство современных технических систем включают в себя подсистемы различной физической природы. При моделировании сложных систем возникает проблема единообразного описания стыковки различных физических процессов.

В основе лежит понятие косвенного подобия: разнородные системы могут быть описаны одинаковыми формальными уравнениями. Отсюда следующая процедура формирования моделей сложных систем:

а. Выделить однородные физические подсистемы.

б. Сформировать эквивалентные схемы этих подсистем.

в. Составить формальное математическое описание подсистем.

г. Установить связи между подсистемами.

При формировании эквивалентных схем используют следующие положения:

1. В каждой подсистеме выделяют элементы (компоненты), состояния которых определяет состояние системы в целом.

2. Выявить связи между компонентами т.е.определить узлы (полюсы) эквивалентных схем. При этом все компоненты делятся на двухполюсные и многополюсные.

В общей теории систем доказано, что любой многополюсный элемент может быть представлен совокупностью двух полюсов, поэтому рассматривают двухполюсный элемент.

3. Состояние каждого узла двухполюсника определяется переменной типа потенциал. Состояние самого двухполюсника определяется двумя переменными U=φ₁-φ₂ и переменная i типа поток.

4. Математическая модель двухполюсника представляет собой компонентное уравнение, связывающее либо U, I, либо i, t.

4.1. Компонент вида C соответствует массе в механических поступательных системах, моменту инерции в механических вращательных системах, емкости в электрических системах, теплоемкости в тепловых системах и гидравлической емкости в гидравлических системах.

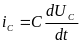
4.2. Компонент типа L соответствует упругости, жесткости в механических системах, индуктивности в электрических системах, гидравлической индуктивности в гидравлических системах.

В эл. схемах: В механических: .

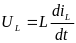
4.3. Компонент типа R соответствует коэффициенту трения в механических системах, активному сопротивлению в электрических системах, теплопроводности в тепловых системах и гидросопротивлению в гидравлических системах.

В эл. схемах: В механических:

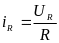
4.4. Компонент типа J соответствует источнику силы в механических поступательных системах, источнику момента в механических вращательных системах, источнику тока в электрических системах, источнику расхода в гидравлических системах.

Обозначение в схемах:

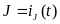
4.5. Компонент типа E соответствует источнику скорости в механических поступательных системах, источнику напряжения (ЭДС) в электрических системах, источнику температуры в тепловых системах и источнику давления в гидравлических системах.

Обозначение в схемах:

5 . Уравнения межкомпонентных связей называют топологическими. Имеется два вида топологических уравнений:

а. условие равновесия в узлах ;

б. условие неразрывности в каждом контуре .

С помощью топологического уравнения осуществляется связь компонентов. Единый вид компонентных и топологических уравнений позволяет создать единое математическое описание систем различной физической природы, следовательно, создать единую методику их моделирования. В результате, например, моделирование механических, тепловых и гидравлических систем можно свести к построению соответствующих электрических цепей.

В результате имеем приблизительно следующую схему:

1. Определение цели моделирования;

2. Формирование основных требований к модели;

3. Выбор свойств оригинала, которые подлежат отражению в модели;

4. Сбор априорной информации об оригинале (знание, опыт, результаты экспериментов и т.д. и т.п.);

5. Синтез структуры модели, т.е. её общего вида без конкретных числовых значений параметров (наиболее сложный и наименее формализованный этап);

6. Параметрический синтез (расчет значений параметров с целью минимизации погрешности);

7. Реализация модели в заданной среде;

8. Исследование модели (физические или вычислительные эксперименты, анализ полученных результатов);

9. Оценка точности, адекватности, экономичности, организация цикла.

Электрическая система:

Механическая система:

Понятие системы. Свойства системы. Типы систем. Характеристики систем.

Физич сист-ма котор мы управляеем наз объкт упр-я его долж описать матем–ки, а закономерности кот подчиняются процессы управления общие для объекта упр-я люб природы поэт мож рассм их общ структ и некое общее мат описание проц упр-я Объект предст не отдельн эл-т, а некую сист-у.

Св-ва системы

Если выполн эти св-ва то это система

1.Целостность и членимость

система – целост совокуп-ть элементов => сист с одн стор целостное образование с др в нем мож выделить отдел элем-ты (выделен-е элем-ты функц-т лишь в данной системе)Для любой сист первичн явл признак целостности т.е. она предст собой что – то еденое целоесостоящ из взаимод-х частей

2.Наличие связей – характерно наличие устойчивых связей между элем-ми или их св-ми превосх по силесвязи с др элем-ми не входящ в дан сист. Особ-ть связи – преобр-е некот велич без изм-я их физич природыОсн харак связи:

*физич наполнение св.(прир св.: инфо, физич, энерг-го поля)*направлен-ть связи(прям, обрат, конрсвязь)*Мощ-т

3.Организация св. – формиров сущест св-й элем-в благодаря их упорядоч распр. во времени и в прост-еПри организ св склад определ структура сист-ы, а св-ва элементов перех в ф-ии

4 Интегратив-е(объедин) качества –св-во кот присуще системе в целом, но не свойствен ни одному из элем сист в отдельности

т.е.сист не сводит к прост совок-ти эл-в и при расчлен сит на элем мы (изуч их св-в)не смож позн св-во сист в целом

Типы систем

1Естественные - сущест в дейст-ти (солнеч, организм)

2.Идеальная – отражает упрощенно действит системы

3.Искуственные сист –ы созд чел-м напр плотина

Характеристики систем

1.Поведение – способ-ть сист-ы перех из одн-го сост в др

2.Равновесие – сп-ть сист при отсут внешн воздейств сохр свое состояние как возможно долго

3.Устойчив-ть-сп-ть сист возвращ в сост равновесия после того как она была вывед из него под дейст-м как-либо возмущений

Понятие управления. Общее уравнение управления. Критерий качества управления. Оптимальное управление. Причины приближенного решения задач моделирования управления. Основные положения при разработке систем управления.

Одна из основных задач – задача управления. Сущность управления это вмешательство в естественный ход протекания какого-либо процесса и изменение его.

Управление – это организация процесса, кот.обеспечивает достижение какой-либо заданной цели. Для любого процесса управления характерны следующие 4 этапа:

1)появление цели

2)оценка ситуации

3)принятие решения

4)исполнение решения

1-ый этап – сбор и обработка информации с целью оценки сложившейся ситуации

2-ой этап – принятие решения о наиболее целесообразных действиях и выдача рекомендаций.

Во многих задачах управления 1-ый этап сбор и обработка информации хорошо обработаны и тогда остаётся только один этап управления – такие задачи носят название одноэтапные или одношаговые. Но в большинстве случаев – это идеализированного решения задачи или идеализирован.управления.

На этапе обработки информации реализация управления сводится к процессу управления конкретными объектами. Тогда физическую систему, пр-ми в кот мы стараемся упростить, будем называть объектами управления. При моделировании объект управления необходимо описать математически. Закономерности кот.подчиняются процессы управления – общие для любых объектов управления любой природы. Поэтому можно рассматривать их общую структуру и общее математическое описание процесса управления.

В системах управления различают несколько классов природы системы:

1)системы естественные – те системы кот.существуют в объективной действительности

2)идеальные системы – системы кот.вымышлены человеком, но отражают действительный мир

3)искусственные системы – системы созданные человеком для своих потребностей.

Решение систем нелинейных уравнений. Метод итерации. Метод покоординатного спуска. Метод градиентного спуска. Метод наискорейшего градиентного спуска. Метод Ньютона.

Общий вид СНАУ можно записать следующим образом:

Для решения СНАУ, прежде всего, нужно выбрать начальную точку, т.е. некий вектор 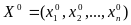. Выбор произволен, но от его качества зависит сходимость численного метода. После этого строится вычислительная процедура, основанная на разложении ф-ции в ряд Тейлора.

Имеем:

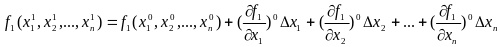
Продолжая дальше:

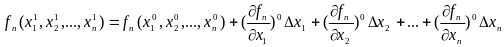
Предполагая, что в т. все n ф-ций равны нулю, получаем систему линейных алгебраических ур-ний относительно ∆x. Определив ∆x_i, осуществляем переход к новой точке:

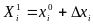
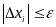
Практическое использование этого метода вызывает огромные сомнения, т.к. на каждом шаге приходится вычислять n² частных производных, что возможно только при наличии аналитических выражений.

Итог: как правило в инженерных расчетах нелинейные ур-ния линеализируют. Для этого используются специальные методы, в частности методы сплайнов.

Методы спуска

Основная идея методов спуска состоит в том, чтобы построить алгоритм, позволяющий перейти из точки начального приближения в следующую точку таким образом, чтобы значение целевой функции приблизилось к минимальному.

Метод покоординатного спуска

Этот метод является редукцией поиска функции многих переменных к последовательности поиска минимумов функции одной переменной. Пусть — начальное приближение к минимуму Φ(u).

Рассмотрим как функцию одной переменной u₁ при фиксированных и находим одним из приведенных методов поиска минимума функции одной переменной

Полученное значение u₁, доставляющее минимум Φ(u₁), обозначим ; при этом

Далее, при фиксированных значениях ищем

как функции от u₂; соответствующее значение u₂ обозначим ; при этом

Этот процесс продолжаем аналогичным образом и для оставшихся координат; в результате получим

Таким образом, переходим из точки u₀ в точку u₁. Этот процесс повторяется до тех пор, пока не будет выполнено условие выхода из итераций, например:

где ε > 0 — заданная точность.

Метод градиентного спуска

Напомним, что градиент функции

есть вектор, ортогональный линиям уровня целевой функции, а его направление совпадает с направлением наибольшего роста Φ(u) в данной точке. В точке минимума grad Φ(u) = 0.

Построим итерационный процесс следующим образом:

где τ — шаг спуска (итерационный параметр). Итерации продолжим до выполнения заданного условия окончания процесса поиска минимума, например

Метод наискорейшего спуска

В методе градиентного спуска выберем шаг τ так, чтобы функция Φ(u) максимально уменьшала свое значение:

В предыдущем примере выбор шага в точке u₀ сводится к задаче о поиске минимума функции

откуда τ = 10/9, поскольку

На следующих шагах τ будет зависеть от .

Метод Ньютона.

Как говорилось выше, метод Ньютона наиболее точный метод решения систем нелинейных уравнений и поэтому наиболее распро­странен. Но для решения системы методом Ньютона необходимо уже иметь приближенное решение данной системы, найденное каким-либо грубым методом.

Пусть существует достаточно близкое решение Х°. Нелиней­ные уравнения системы (3.5) линеаризуются путем разложения их в ряд Тейлора в точке Х°, ограничиваясь членами 1-го порядка малости:

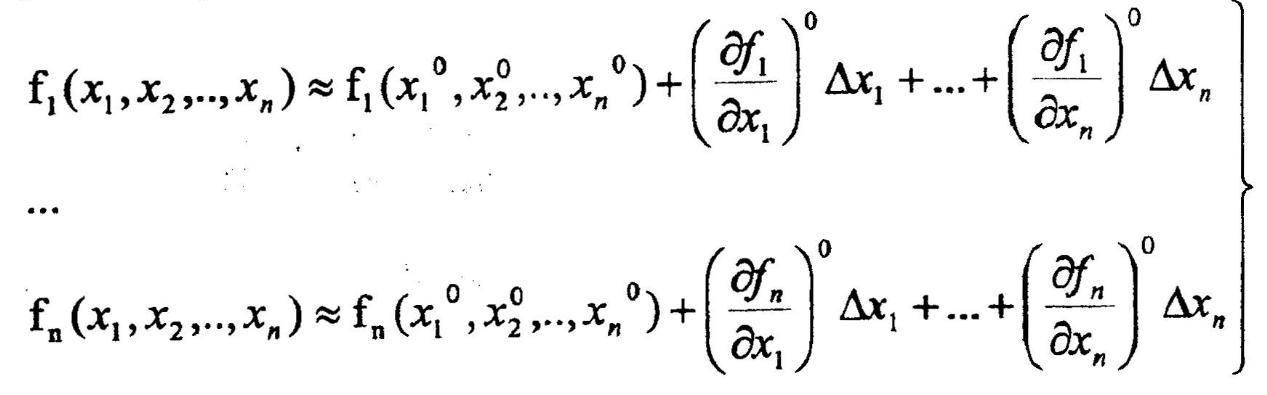
Получаем систему n линейных уравнений относительно неизвестных

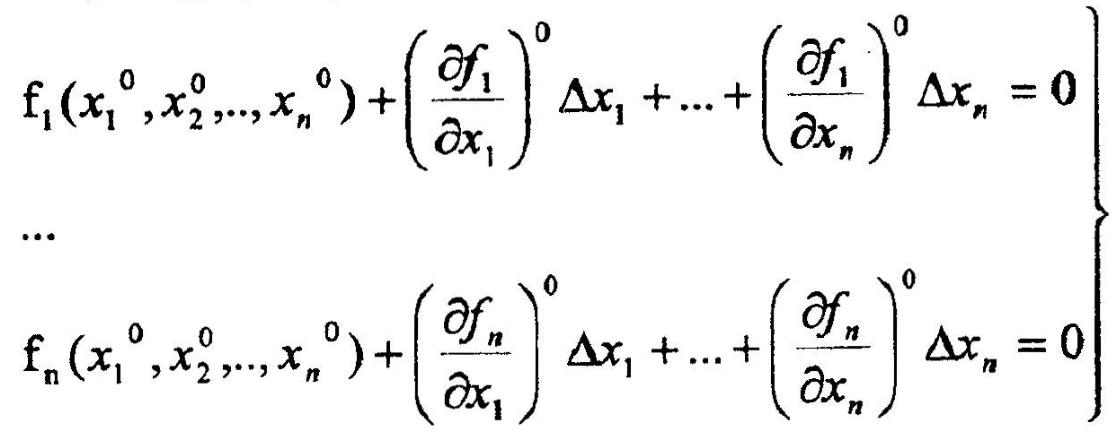
Что равносильно:

Обозначаем:

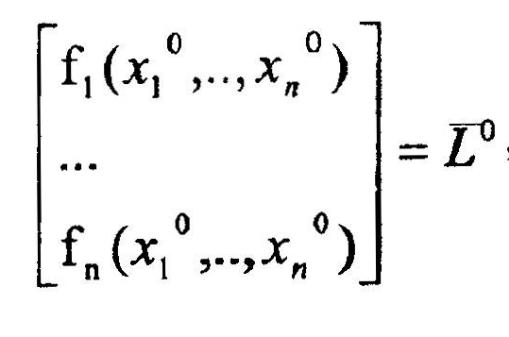
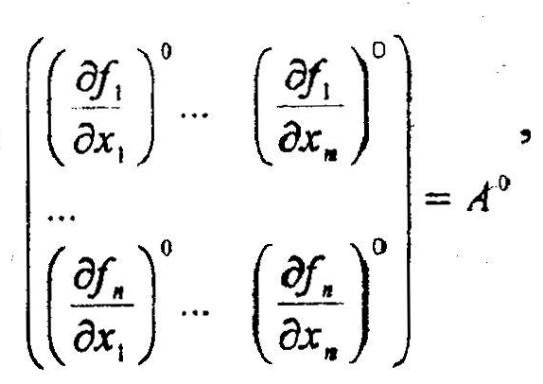
получаем систему в векторном виде:

Решая эту систему (необходимым условием решения является невырожденность матрицы А), получим вектор ∆X¹ , который приводит нас к новой точке X¹ решения заданной системы:

Решение системы с точностью до ε будет точка Х^*=Х ^к

Понятие интерполяции. Виды интерполяции. Конечные и разделенные разности. Их свойства и применение. Интерполяция параболическими полиномами по методу Ньютона и методу Лагранжа. Понятие сплайн – интерполяции. Интерполяция сплайнами второго порядка.

Интерполяция функции – построение достаточно простой для вычисления ф-ции (х) совпадающей в заданных узлах со значением ф-ции f(x), а в остальных точках заданного отрезка [a,b] приближенно представляющей ф-цию f(x) с заданной точностью.

[x0,x1,x2]=([x1,x2]-[x0,x1])/(x2-x0) разделенные разности 2-го порядка

[x1,x2,x3]=([x2,x3]-[x1,x2])/(x3-x1)

конечные разности записываются так же в таблице. Для полинома f(x) степени n разделённые разности n-го порядка есть константы, которые не зависят от узлов и равны коэффициенту при старшей степени х, все разделенные разности порядка больше чем n тождественно равны нулю. Степень интерполяционного полинома в случае неравно отстоящих узлов выбирается так, чтоб она совпадала с порядком практически постоянных разделенных разностей.

Существует несколько видов интерполяции: 1. линейная 2. круговая 3. винтовая 4. сплайнами

Интерполяционные полиномы в форме Ньютона удобно использовать, если точка интерполирования находится вблизи начала (прямая формула Ньютона) или конца таблицы (обратная формула Ньютона).

Многочлен Ньютона:

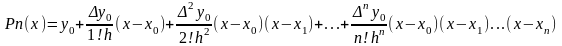
Где

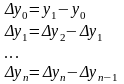и

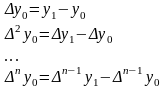
Конечные разности

Способ Лагранжа

Пусть ф-ция задана таблично. Ищем полином в виде: f(x)=yi*Li(x) Li(x) – коэффициент Лагранжа (полином влияния)

Св-ва: а)степень равна к б) Li(x)=1, если x=xi; Li(x)=0, если x=xj (j<>i)

Li(x)=(x-x0)(x-x1)… (x-xi-1)(x-xi+1)…. (x-xn)

(xi-x0)(xi-x1)… (xi-xi-1)(xi-xi+1)… (xi-xn)

По теореме из Анализа существует единственный полином к-ой степени походящий через заданные точки, видно что найденный полином Лагранжа является единственный полиномом.

Достоинства: коэффициенты Лагранжа зависят только от х. При больших сериях опытов, если х-ы постоянны, то коэффициенты Лагранжа можно вычислять всего один раз.

Недостатки: допустим для к точек составили полином Лагранжа. В случаи добавления или изменения 1 точки нужно пересчитывать все коэффициенты Лагранжа заново.

Сплайн (англ. spline - рейка, линейка) - это определенная в некоторой области G ∈ Rⁿ кусочно-полиномиальная функция из класса C^r(G).

Таким образом в соответствии с определением существует разбиение области G на подобласти такое, что внутри каждой подобласти сплайн представляет собой полином некоторой степени М.

Параболическая сплайн интерполяция:

Классический подход основывается на требовании строгого совпадения значений 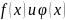в точках

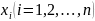
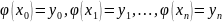(1)

Будем искать интерполяционную функцию 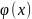в виде полинома степени n

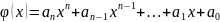(2)

Этот полином имеет (n+1) коэффициент. Естественно предположить, что (n+1) условий (1), наложенные на полином (2), позволяют однозначно определить его коэффициенты. Действительно, требуя для выполнения условий (1), получаем систему (n+1) уравнений с (n+1) неизвестной.

(3)

Решая эту систему относительно неизвестных 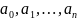мы получим аналитическое выражение полинома (2). Система (3) имеет единственное решение, т.к. ее определитель отличен от нуля.

Отсюда следует, что интерполяционный полином для функции 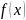, заданной таблично, существует и единственен.

Второго порядка

Пусть заданы точки: (x₀;y₀), (x₁;y₁), … , (xn;y_n), и пусть непрерывна первая производная. На каждом интервале [x_i;x_i+1] найдём интерполяционный сплайн S_2i=c_i+b_i(x-x_i)+a_i(x-x_i)².

Для нахождения i-го сплайна надо решить систему уравнений:

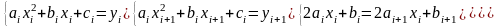
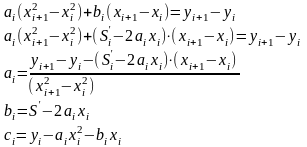
Где

Понятие аппроксимации. Критерии близости. Метод наименьших квадратов. Аппроксимация параболическими полиномами. Аппроксимация ортогональными полиномами по методу наименьших квадратов (НК). Аппроксимация показательными полиномами по методу НК. Аппроксимация тригонометрическими полиномами по методу НК.

f(x) задана таблично на [a,b]. Процесс апроксимации это построение полинома проходящего в близи этих точек, сглаживающего их.По исходным данным подобрать такую аналитическую ф-ю φ (х), где х є[a,b], которая имела бы простую структуру и сглаживала бы исходные даные и как можно лучше отображала ф-ю f(x). Это процесс назыв. апроксимацией. Интерполяция это частный случай апроксимации. При апроксимации используются различные классы ф-й (это степен.ф-и, тригоном-е ф-и.). Он выбирается из физического смысла задачи. Степень полинома k<n (кол-во точек) т.к точность от нас не требует точного совпад-я в узлах апроксимации.

Сущест-ют две меры близости f(x) к φ (х). 1) δ²=_i=0Σⁿ(φ(х_i)-f(x_i))² 0 Нам необходимо найти min этой ф-и т.е сумма квадратов отклонения в узлах апроксимации должна быть min. Это метод наимен. квадратов.2)Δ=max|φ(х_i)-f(x_i)|→ 0 max отклонения апроксимирующей ф-ии должно быть min. Это равномер. апроксимация. Он использ. редко.

Методом наим-ых квадратов(МНК). О качестве полученной апроксимации можно судить по величене уклонений

Vi=| φ(х_i)-f(x_i)|, i=0…n. Если мы составили апроксимирующий полином, вычислили отклонения для всех узлов и эти уклонения нас не устраивают, то нам необходимо увеличить степень полинома с k до k+1.Это приводит к повтору всех проделанных вычислений. Поэтому желательно найти способ составления всех апроксимир-их полиномов от кот. Легко перейти от k к k+1 без сложных вычислений.

Пусть дана n+1 ф-ця f(x) – задана таблично

X: X0; X1… Xn

Y: Y0; Y… Yn

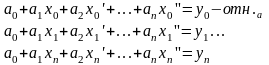
получаем полином

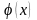
Аппроксимация парабол полиномом

F(x): x₀=a, x₁, x₂, ..., x_n=b

y₀, y₁, y₂, ..., y_n

(x) = a₀ + a₁x + ... + a_kx^k k<n

Составляется целев ф-ция по МНК

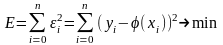
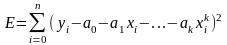
Частные произв равны 0 – сост-м систему

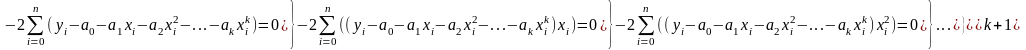
Решив систему получим коэффициенты для полинома (x) = a₀ + a₁x + ... + a_kx^k

Аппроксимация показательным полиномом

Имеются узлы аппроксимации: x0 x1 x2 … x

y0 y1 y2 … yn

Из теории д.у. известно что решением нелин. д.у. n-го порядка является показат полином, причем степень полинома совпадает со степенью д.у.

Ищем д.у., решением кот-го явл-ся показат полином

Рассм полином 2-й степени

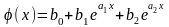
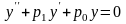
В реальных задачах

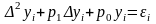
Поиск коэффицентов a1, a2:

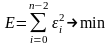
E=∑(Δ²yi+p1*Δyi+p0*yi)² i=0,…,n-2

Δyi=y(i+1)-yi Δ²yi=y(i+2)-2y(i+1)+yi

dE/dpo=0

dE/dp1=0

В результате получаем СЛАУ. Решаем ее.

λ1=-p1/2+(p1²/4-p0)½

λ2=-p1/2-(p1²/4-p0)½

Находим искомые коэффициенты:

a1=ln| λ1|

a2=ln| λ2|

Поиск коэффицентов b0, b1, b2:

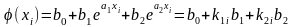
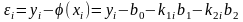
E=∑(yi-b0-k1i*b1-k2i*b2)² i=0,…,n

k1i=exp(a1*xi) k2i=exp(a2*xi)

dE/db0=0

dE/db1=0

dE/db2=0

В результате получаем СЛАУ. Решаем ее.

_{Аппроксимация ортогональными полиномами по методу наименьших квадратов (НК).}

Аппроксимирующую функцию будем искать в виде

для этого необходимо

1. Составить ортогональные полиномы

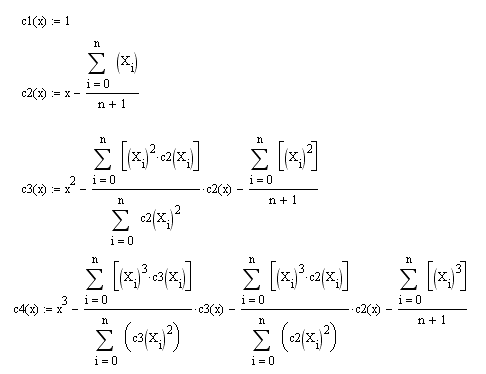
и так далее до необходимого порядка точности

2. Вычислить коэффициенты Фурье

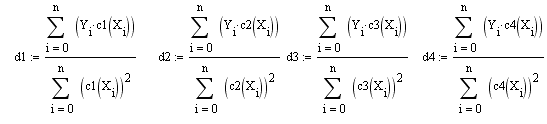
Здесь массивы X и Y – массивы экспериментальных значений

П ри аппроксимации тригонометрическим полиномом в качестве базовой аппроксимирующей выбирается:

где m-порядок полинома.

Коэффициенты полинома определяются на основании метода наименьших квадратов при минимизации среднеквадратического отклонения:

Тогда коэффициенты тригонометрического полинома определятся по формулам:

где j=0,1,2…m.

Сначала устанавливается минимальный порядок ряда m=1, а потом увеличивается, пока не будет достигнута требуемая точность.

Понятие численного интегрирования. Нахождение интеграла методом прямоугольников, методом трапеций, методом Симпсона.

В ряде случаев невозможно найти аналитически праобраз перваобразную, даже если находится, то бывает она грамозка для вычисления. Или ф-я задана таблично. В определении интегралов уже заложена основная идея численого интегрирования.

Пусть функция f(x)вещественная определена на (ab) разобьем ab на x₀x₁…x_n в каждом интервале x_i;x_i+1. Произвольно выбираем O_i . 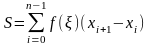Если сущ-ет предел - это будет значения интеграла можем предположить S=I. Можно оценить |I-S|=S₂-S₁ – S₂,S₁ сумы верхняя и нижняя ф-ии

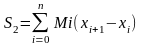
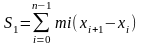
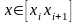
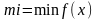
Ф-лы численного интегрирования много сущ-ет они отличаются

Выбором точек x_i,O_i

Скоростью сходимости

Оценка погрешности – используется в том случае если что либо известно о ф-ии F(x). Если неизвестно то вычисления S происходит по определению интеграла

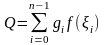
Пусть O_i – узлы X_i+1-X_i=g_i вес ф-ии веса не зависит от значения y_i, тогда 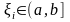и тогда S=Q+R, где R- отвечает за погрешность в-я интеграла. S=Q+R -эта ф-ла носит название квадратурная ф-ла.

С читается, что квадр. Ф-ла задана если указано как вибирать O_i, g_i и как рассчитывать R

1 Формула прямоугольников.

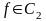
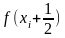
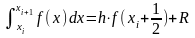
- ф-ла для одного шага Если 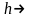0 то погрешность 0. И погрешность

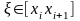
При использовании ф-лы прямоуг значение ф-ии вычисляется 1 раз Если перейти к интервалу [ab]

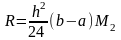, где 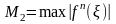-взятое со своим знаком.

2 Формула Трапеции

на

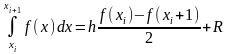
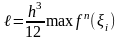
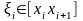
в формуле трапеции ф-ии f(x) вычисляются 2 раза и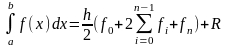

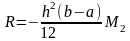
где

3 Формула Симпсона

Кривая f(x)на интервале заменяется параболой проходящей через 3 точки

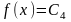
На интервал строится 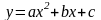тогда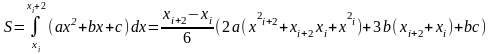

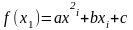
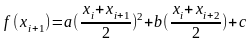
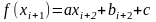
Запишем сочетание

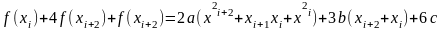
видим, что

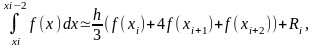
где

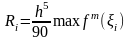
Для ф-лы Симпсона Значение ф-ии вычисляются трижды

где где

По виду оценки погрешности для всех 3х случаев сделаем вывод

1 чем больше [a,b], тем больше ошибка интегр-ия.

2 чем меньше h, тем меньше ошибка инт-ия.

Для данного случая существует насыщенность метода, так при уменьшении h,R на некотором значении увеличивается.

Решение обыкновенных дифференциальных уравнений. Методы решения. Задача Коши. Краевая задача. Решение ОДУ методом Эйлера, модифицированным методом Эйлера, методом Рунге – Кутта, методами прогноза и коррекции. Решение ОДУ большого порядка. Решение систем ОДУ. Методы решения краевых задач

Основные понятия.

Ур-ния, содержащие неизвестную ф-цию под знаком производной, называются дифференциальными уравнениями.

Классификация ДУ осуществляется по ряду признаков:

1. Если ур-ние содержит одну независимую переменную и производную по ней =>ОДУ. Если две и более и производные по ним, то ДУРЧП

2. Порядок старшей производной.

Различают ДУ первого, второго и т.д. порядков.

3. Если зависимая переменная входит в первой степени, то имеем линейные ДУ, в противном случае – нелинейные ДУ.

Решить ОДУ – это значит найти некоторую ф-цию, которая удовлетворяла бы как самому ур-нию, так, возможно, дополнительным условиям.

В зависимости от дополнительных условий различают задачу Коши и краевую задачу.

Для решения задачи Коши существует набор хорошо апробированных методов, а решение каждой отдельной краевой задачи может потребовать специфических подходов. Поэтому в классической вычислительной математике рассматривают вычисления задачи Коши, которую в простейшем случае можно рассмотреть следующим образом:

Задано ОДУ первого порядка: 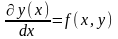и начальное условие: y(x₀)=y₀. Требуется найти ф-цию, удовлетворяющую как уравнению, так и начальному условию.

Численные методы для решения этой задачи могут быть разбиты на две группы: одношаговые и многошаговые.

Одношаговый метод.

В основе всех одношаговых методов лежит разложение ф-ций в ряд Тейлора:

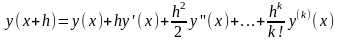, в котором сохраняются члены до установленного порядка. Если сохраняется член вида , то говорят, что метод имеет порядок n, а погрешность метода пропорциональна hⁿ⁺¹. Для нахождения следующей точки y(x^k+1) требуется информация только об одной предыдущей точке y(x^k) – способность самостартования.

Простейшим представителем одношаговых методов является метод Эйлера.

y(x+h)=y(x)+hy’(x)+O(h²)

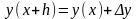
В результате имеем общую формулу метода Эйлера:

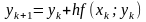
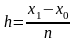y(x₀)=y₀, k=0,1,2,…

Несомненное преимущество метода Эйлера – простота реализации. Существенный недостаток – крайне низка точность, которую, однако, можно заранее оценить. Как правило, для повышения точности осуществляют решение с шагом h, с шагом h/2 и т.д. В этом случае процедуру называют самоконтролирующей или с автоматическим выбором шага.

Модификации метода Эйлера

Приведенный метод Эйлера можно улучшить, незначительно увеличив сложность вычислений, при этом повысится точность реше­ния.

Будем рассматривать дифференциальное уравнение того же

вида: y'=F(x,y) с начальным условием у(х₀)=у₀

1 шаг. Выбираем фиксированное приращение аргумента h=(Xf-Xo)/n, где Xf - Конечная точка интервала интегрирования, n - число шагов.

2 шаг. Применяя процедуру модиф-го метода Эйлера, вычисляем у_к по рекуррентной формуле:

Все остальные одношаговые методы базируются на идее Эйлера, но для значительного повышения точности используются дополнительные точки.

Классическим считается метод Рунге-Кутта четвертого порядка точности.

y_n+1=y_n+1/6(k₀+2k₁+2k₂+k₃)

k₀=hf(x_n;y_n)

k₁=hf(x_n+1/2h;y_n+1/2k₀)

k₂=hf(x_n+1/2h;y_n+1/2k₁)

k₃=hf(x_n+1/2h;y_n+k₂)

Ошибка пропорциональна O(h⁵).

Этот метод сочетает простоту реализации с достаточной точностью в связи с чем он стал базовым во всех библиотеках математических программ. Для повышения точности в основную процедуру добавляют механизм половинного деления.

ОДУ высших порядков. Системы ОДУ.

Если есть ОДУ порядка P, то последовательные замены переменных его можно свести к системе из P ОДУ первого порядка, которая в общем случае имеет вид:

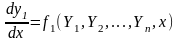Y₁(0)=Y₁₀

…

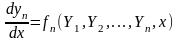Y_n(0)=Y_n0

Для решения C в системе ОДУ могут быть использованы методы, рассмотренные для решения отдельного уравнения.

Сложность заключается в том, что ф-ции f_i могут иметь абсолютно разные динамические характеристики, а независимая переменная x одна, поэтому шаг интегрирования выбирается для всех ф-ций, что в конечном итоге может привести к катастрофическому накоплению погрешности ошибок. Особая проблема – решение краевых задач. Постановка краевой задачи отличается наличием дополнительных условий прохождения кривой y(x) через все точки. Как правило, для поиска решения используют метод «стрельбы».

Методы прогноза и коррекции.

При использовании методов прогноза и коррекции одного порядка точности их погрешности выражаются через одну и ту же старшую производную искомой функции. Так, для

методов второго порядка прогноз дает

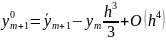
Коррекция:

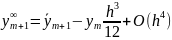
Исключая из этих соотношений неизвестное истинное решение , можно выразить третью производную (а значит и погрешности методов прогноза и коррекции) через значение (прогноз) и стационарную точку коррекции

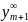
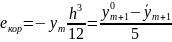
Т. о., если после проведенных корректирующих итераций взять значение

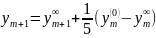
то погрешность (m + 1)-го шага будет уже

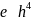
Преимущества.

• Использование информация о предыдущих уже пройденных точках (не требуется до-

полнительных расчетов, как в методах Рунге–Кутты).

• Высокая точность расчета.

Недостатки.

• Методы являются несамостартующими.

Для запуска вычислений, на первых нескольких узлах необходимо использовать дру-

гой (одношаговый, самостартующий) метод, например, метод Рунге–Кутты.

Решение дифференциальных уравнений в частных производных (ДУЧП). Конечно-разностные методы решения. Решение стационарного, одномерного волнового уравнения, одномерного уравнения теплопроводности.

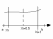
Модель длинной линии. Телеграфные и волновые уравнения.

На рисунке изображена эквивалентная схема отрезка длинной электрической линии провода кабеля и т.д. и т.п.

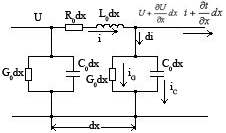
R₀, L₀, C₀, G₀ – погонные параметры, dx – длина отрезка, который мы рассматриваем.

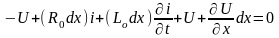
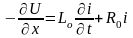(1)

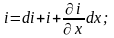
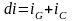
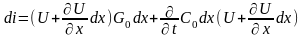
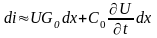
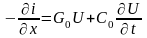(2)

Продифференцируем обе части уравнения по dx:

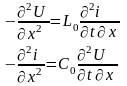
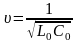
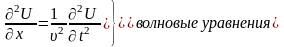
Телеграфные уравнения представляют собой ДУЧП первого порядка, а волновые ДУЧП второго порядка. Решая эти уравнения тем или иным численным методом можно получить кривые изменения токов и напряжения как во времени, так и по длине.

Решение стационарного уравнения разностным методом

Решение ищется в области D с границей Г. Пусть a > 0 , b > 0 , g <= 0 в D

Заданы граничные условия: 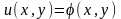для всех

Покроем обл D сеткой параллельных прямых: 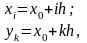где

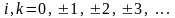
Точки пресечения прямых – узлы. Узлы внутри D- внутренние, если хотя бы один соседний узел данного узла вне области D, то узел – граничный.

Заменим производные во внутренних точках уравнениями по шаблону «крест»

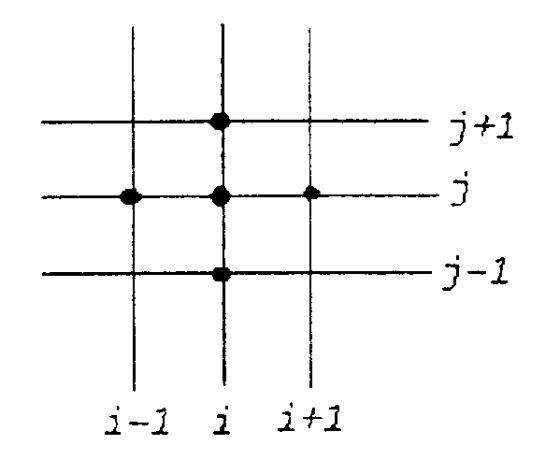
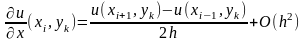
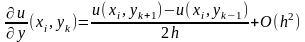
Подставим в исходное уравнение отбросив погрешность

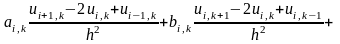
Такое уравнение составляется для каждой внутренней точки

Далее рассм граничные точки. Значения в них вычисляются в зависимости от того какая из 4-х точек пересечения границы обл D ближе к нашей гр точке 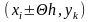или

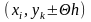
Получим или

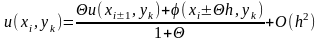
Или

Отбросив погрешность получим уравнение для нраничной точки.

Такое ур-е сост-ся для всех точек.

Решение системы из ур-й для внутренних и граничных точек есть решение исходного уравнения

Решение волнового уравнения конечно-разностным методом

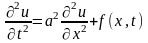
Где

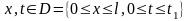
Заданы граничные условия: оба конца закреплены

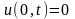
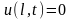
Заданы начальные условия:

Начальная форма струны

Начальная скорость точек струны

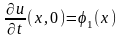
Покроем обл D сеточной областью

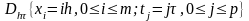
где m=l/h; p=t₁/τ

Заменим производные во внутренних точках уравнениями по шаблону «крест»

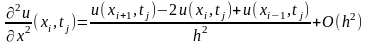
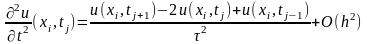
Подставим в исходное уравнение отбросив погрешность

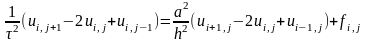
где i=1,m-1; j=1,p-1

Добавим начальные условия:

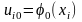
де i=0,m

и граничные условия:

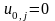
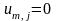
где j=0,p

Получили СЛАУ относительно узлов сетки

Для волнового ур-я можно найти реш-я, не решая системы. Для этого необходимо явно выразить переменные любого временного слоя, через предыдущие слои:

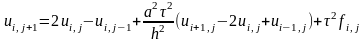
Для первого слоя находим из начальных условий, для второго – из первого слоя и т. д.

Пока не будет достигнут нужный слой. Нужно помнить о том, что переменные для всех слоев вычисляются исходя из гран. усл. Данная схема работает устойчиво при

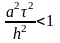
Решение уравнения теплопроводности разностным методом

где

Начальные условия: начальное распределение температур

где

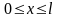
Граничные условия: температурные решения на концах стержня

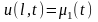
Покроем обл D сеточной областью

где m=l/h, p=t₁/τ

Запишем уравнения для внутренних точек основываясь на 3-х шаблонах: явном, неявном четырехточечных и неявным шеститочечным

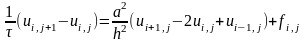
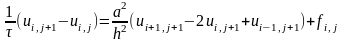
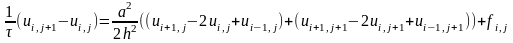
Первые две схемы условно сходимы, а третья – Кранка-Николсона – сходима безусловна и более применима.

Переход от нулевого слоя к 1-му выполняется за счет нач усл.

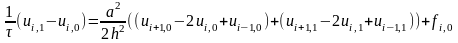
После преобразований:

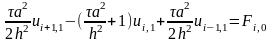
Где

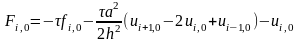
Добавив граничные условие получим систему лин ур-й. Решив ее получим зн-я переем-х на 1-м слое.

Аналогично зн-я переем считается для 3-го, 4-го слоев и т. д. до нужного слоя

Проекционные методы решения ДУЧП. Вариационный принцип. Дискретизация Ритца. Проекционная постановка. Метод конечных элементов.

Большой класс методов решения УрЧП носит название проекционных ме­тодов, которые включают в себя вариационные методы и собственно проекционно-разностные методы.

Вариационные методы

Эти методы применяются для решения задач, которые могут быть описаны с помощью так называемых вариационных принципов. Простейший из них - функция и(х), являющаяся решением задачи, должна быть стационарной точкой вариационного функционала

где функция и принимает на границе Г области D значения :

Функционалом называется оператор, который ставит число в соответствие функции, а стационарная точка функции (функционала) - точка локального минимума этой функции

Поиск стационарной точки функционала сводится к решению дифференциального уравнения, называемого уравнением Эйлера:

неизвестные коэффициенты

некоторые фиксированные линейно независимые функции, назы­ваемые базисными.

Метод Ритца заключается в том, что задача решается не на всем пространстве U функций u(х,у), заданных на области D для которых определен функционал I(u), а только на m-мерном подпространстве U^m, состоящем из всевозможных линейных комбинаций элементов e_i(x,y). В этом случае приближенное решение получаем в виде минимума функ­ционала

Необходимое условие минимума есть которое дает т урав­нений для нахождения а_i. Если система разрешима, то находим величину и_т

Задача может быть сформулирована как вариационная только в том случае, если для этой задачи выполняется уравнение Эйлера. Но этим свойством обладают далеко не все задачи. В этом случае можно использовать проекцион­ную постановку, для которой не требуется выполнения данного условия.

Пусть дана функция в области D

(5.11)

которая принимает на границе Г области D значения

Пусть также дана некоторая произвольная непрерывная на D функция называемая пробной функцией, которая обращается в ноль на границе Г области D. Умножая уравнение (5.11) на функцию и интегрируя полу­ченное равенство по , получим интегральное тождество

(5.12)

Таким образом, задачу (5.11) можно сформулировать в следующей проек­ционной постановке. Требуется найти такую функцию и(х,у) , которая удовле­творяет интегральному тождеству (5.12) для произвольной пробной функции и удовлетворяет заданным краевым условиям.

Проекционная постановка краевой задачи используется в случаях уравне­ний с разрывными коэффициентами, а также для функций и(х,у), не имеющих второй производной.

Приближенное решение задачи в проекционной постановке, называемое методом Галеркина, ищется в виде функции

неизвестные коэффициенты

которая удовлетворяет интегральному тождеству (5.12) для любой пробной функции , тем самым задача сводится к решению системы уравнений

В общем случае применение методов Ритца и Галеркина к решению крае­вых задач приводит к необходимости решения системы уравнений с заполненными матрицами. Современный вариант проекционных методов, носящий на­звание «метод конечных элементов», не имеет такого недостатка. Можно вы­делить характерные черты, выделяющие этот метод среди других проекцион­ных методов:

1)Расчетная область (область определения независимой переменной) разбива­ется на конечное число элементарных подмножеств стандартной формы (кото­рые и называются конечными элементами).

2) Используемые базисные функции e_i(x,y) таковы, что они на каждом элемен­те имеют простой вид (чаще всего - многочлены) и отличны от нуля лишь на нескольких соседних элементах

Понятие оптимизации. Типы задач оптимизации.

Оптимизация (optimus – наилучший) подразумевает выбор наилучшего варианта решения среди некоторого множества допустимых вариантов.

Если выбора нет, то и оптимизации нет.

Если есть выбор, то должно быть некое правило предпочтения одного варианта другому. Это правило получило название критерий (от лат. Criterion -оценка).

В основе построения критерия лежит понятие целевой функции F_ц (функции качества), которая количественно выражает те или иные свойства (качества) реального объекта.

Любая задача оптимизации реальных объектов имеет 2 аспекта:

1. Нужно формализовать понятия наилучший, оптимальный, т.е. физическую постановку задачи превратить в математическую: сформировать целевую функцию и ограничения.

2. Нужно решить полученную математическую задачу наиболее эффективным методом.

1 аспект подразумевает знание предметной области.

2 – научный.

Область математики, изучающая теорию и методы решения задач оптимизации (определение экстремума функции) называется математическим программированием.

Классификация задач математического программирования основана на специфике функций и ограничений.

В зависимости от количества независимых переменных различают одномерные и многомерные задачи.

В зависимости от вида функции различают линейное и нелинейное программирование.

В зависимости от числа экстремумов рассматриваемой области различают задачи локальной (1 экстремум) и глобальной (много экстремумов) оптимизации.

В зависимости от наличия или отсутствия ограничений, накладываемых на независимые переменные, различают задачи на условные и безусловные экстремумы.

Задача наилучшего приближения.

Если рассматривать систему n линейных уравнений с m неизвестными 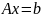в случае, когда она переопределена, то иногда оказывается естественной задача о нахождении вектора x, который "удовлетворяет этой системе наилучшим образом", т. е. из всех "не решений" является лучшим. Например, бывает полезной задача о нахождении вектора x, для которого разность правой и левой частей системы (невязка) минимальна, т. е. минимальна функция

(1) Эту задачу символически записывают в виде .

Норму в (1) можно брать разную. Например, если взята евклидова норма, то получается задача о наилучшем квадратичном приближении

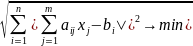или, что эквивалентно,

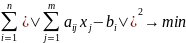
Геометрически эта задача интерпретируется как задача о нахождении на гиперплоскости A(R^m) в пространстве Rⁿ точки, ближайшей к точке b = (b₁, ..., b_n).