2. Задача Штейнера.

Классическая формулировка: требуется найти точку x ∈ R^m, сумма расстояний от которой до заданных точек x¹, ..., xⁿ ∈ R^m минимальна. Эта задача типично оптимизационная:

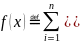
Задачи 1 и 2 - задачи безусловной оптимизации — на искомое решение не налагается никаких дополнительных условий, кроме того, что оно должно доставлять минимум некоторой функции (минимум функции ищется на всей области определения функции). Чаще встречаются задачи условной оптимизации:

3. Задача о рационе.

Пусть имеется n различных пищевых продуктов, содержащих m различных питательных веществ. Обозначим через a_ij содержание (долю) j-го питательного вещества в i-ом продукте, через b_j — суточную потребность организма в j-ом питательном веществе, через c_i — стоимость единицы i-го продукта. Требуется составить суточный рацион питания минимальной стоимости, удовлетворяющий потребность во всех питательных веществах. Если обозначить через x_i суточное потребление i-го продукта, то эта задача может быть формализована следующим образом. Нужно минимизировать функцию 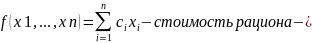при условиях 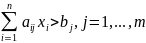(рацион должен содержать не менее суточной потребности в каждом из питательных веществ). 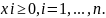Очевидно, также следует требовать, чтобы В векторных обозначениях задача о рационе может быть записана так: минимизировать функцию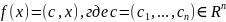 ; эту задачу, как обычно, мы записываем в виде где c = (c₁, ..., c_n) ∈ Rⁿ; эту задачу, как обычно, мы записываем в виде (c, x) → min при ограничениях Ax ≥ b, x ≥ Θ.

В них первое неравенство связывает два вектора Ax и b из R^m, а второе – два вектора x и Θ из Rⁿ.

Θ - нуль пространства R^m - m-мерного вещественного линейного.

4. Транспортная задача.

Эта задача - классическая задача линейного программирования. К ней сводятся многие оптимизационные задачи. Формулировка: на m складах находится груз, который нужно развезти n потребителям. Пусть a_i (i = 1, ..., n) - количество груза на i-ом складе, а b_j (j = 1, ..., m) - потребность в грузе j-го потребителя, c_ij - стоимость перевозки единицы груза с i-го склада j-му потребителю. Требуется минимизировать стоимость перевозок. Если обозначить через x_ij объем перевозок с i-го склада j-му потребителю, то транспортная задача формализуется так: 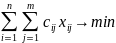, 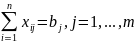(все потребители должны быть удовлетворены),

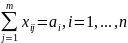(весь груз должен быть доставлен потребителю),

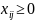(нельзя перевозить груз от потребителя на склад).

3,4 - линейные задачи условной оптимизации. 5 - нелинейная.

5. Задачи о распределении ресурсов.

Общий смысл таких задач — распределить ограниченный ресурс между потребителями оптимальным образом. Рассмотрим простейший пример — задачу о режиме работы энергосистемы. Пусть m электростанций питают одну нагрузку мощности p. Обозначим через x_j активную мощность, генерируемую j-ой электростанцией. Техническими условиями определяются возможный минимум μ_j и максимум M_j вырабатываемой j-ой электростанцией мощности. Допустим затраты на генерацию мощности x на j-ой электростанции равны e_j(x). Требуется сгенерировать требуемую мощность p при минимальных затратах. В наших обозначениях

,

,

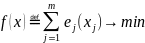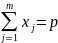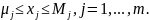
Если обозначить 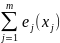через , через g(x), а через Ω, то эта задача переписывается так

.

Признаки классификации.

Один из классификационных признаков делит оптимизационные задачи на два класса: задачи безусловной оптимизации и задачи условной оптимизации. Первые из них характеризуются тем, что минимум функции f: R^m → R ищется на всем пространстве:

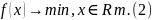
В задачах же второго класса поиск минимума идет на некотором собственном подмножестве Ω пространства R^m:

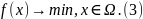
Множество Ω часто выделяется ограничениями типа равенств

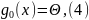
где g₀: R^m → R^k, и/или ограничениями типа неравенств 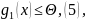где g₁: R^m → R^l.

Другой классификационный признак задач оптимизации — свойства функций f и множеств Ω. Линейные задачи - функция f — аффинная, а множество Ω — многогранное (множество Ω называется многогранным, если оно выделяется ограничениями вида (4) и (5) с аффинными функциями g₀ и g₁). Квадратичные задачи оптимизации - функции f, g₀ и g₁ квадратичные.

Задачи выпуклого программирования - функции f, g₀ и g₁ выпуклые. В общем случае говорят о задачах нелинейного программирования. В таких задачах обычно предполагается гладкость фигурирующих в них функций.

Линейное программирование (ЛП). Геометрическая интерпретация задачи ЛП. Примеры задач ЛП.

Линейное программирование — математическая дисциплина, посвященная теории и методам решения задач об экстремумах линейных функций на множествах n-мерного векторного пространства, задаваемых системами линейных уравнений и неравенств.

Обобщенная постановка задачи линейного программирования

В самом общем случае задача линейного программирования формализуется следующим образом:

Найти экстремум некой функции F(x) вида

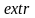
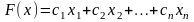
где

n – кол-во независимых переменных

m – число ограничений

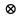- операция отношения типа

m n

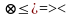
Как правило общая задача тем или иным способом сводится к канонической форме (все ограничения имеют вид равинства).

Симплекс-метод - алгоритм решения задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве. Метод был разработан американским математиком.

Суть метода заключается в следующем: в n-мерном пространстве строится исходный симплекс, в вершинах которого вычисляются значения целевой функции. Если ищется минимум, то отбрасывается вершина, в которой функция имеет max значение; если ищется максимум, то отбрасывается вершина, в которой функция имеет min значение, и строится новый симплекс.

Транспортная задача

Имеется некий однородный груз, который нужно перевести с n складов на m заводов. Для каждого склада i известно, сколько в нем находится груза ai, а для каждого завода известна его потребность bj в грузе. Стоимость перевозки пропорциональна расстоянию от склада до завода (все расстояния cij от i-го склада до j-го завода известны). Требуется составить наиболее дешевый план перевозки. Решающими переменными в данном случае являются xij — количества груза, перевезенного из i-го склада на j-й завод.

Ограничениями будут и

.

Целевая функция имеет вид: , которую надо минимизировать.

Нелинейное программирование (НП). Аналитические условия решения задач НП. Типы методов НП. Методы решения задач одномерной минимизации. Метод дихотомии. Метод золотого сечения. Методы решения задач многомерной оптимизации. Метод деформируемого многогранника Нелдера-Мида.

Многомерную задачу нелинейного программирования в общем случае нужно сформулировать следующим образом:

Найти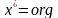

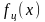
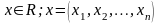
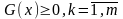- ограничения

и граничные условия:

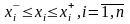
При этом G_k(x) могут быть как линейными, так и нелинейными функциями.

Все методы решения задач нелинейного программирования основаны на необходимых и достаточных условиях существования экстремума функции.

Функция f(x) – ищется локальный минимум

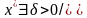при любых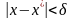

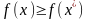
Раскладывая одномерную функцию в ряд Тейлора:

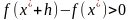
1)

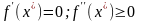
условие существования минимума локальной функции.

В многомерном случае имеем:

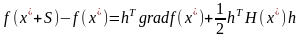
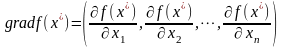
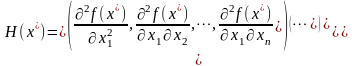
а)

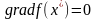
б)

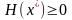
Для решения задачи нелинейного программирования без ограничений разработан ряд численных методов:

1) Методы нулевого порядка: используют только информацию о самих значениях функции (метод перебора, метод случайного поиска).

2) Методы 1 порядка: Кроме информации о значениях функции пытаются использовать информацию о ее градиенте (градиентные методы).

3) Метод 2 порядка: кроме информации о значениях функции пытаются использовать информацию о ее первых 2 производных (методы Ньютона).

Методы нулевого порядка просты в реализации, но не точны и бездоказательны.

Методы 2 порядка доказательны, но предельно сложны в реализации.

Аналитическое условия решения задач НП.

Типы методов

1)0-го порядка – только значения самой ф-ции f

2)методы 1-го порядка – значения f,f^|

3)методы 2-го порядка – значения f, f^| ,f^||

Метод деления пополам (метод дихотомии)

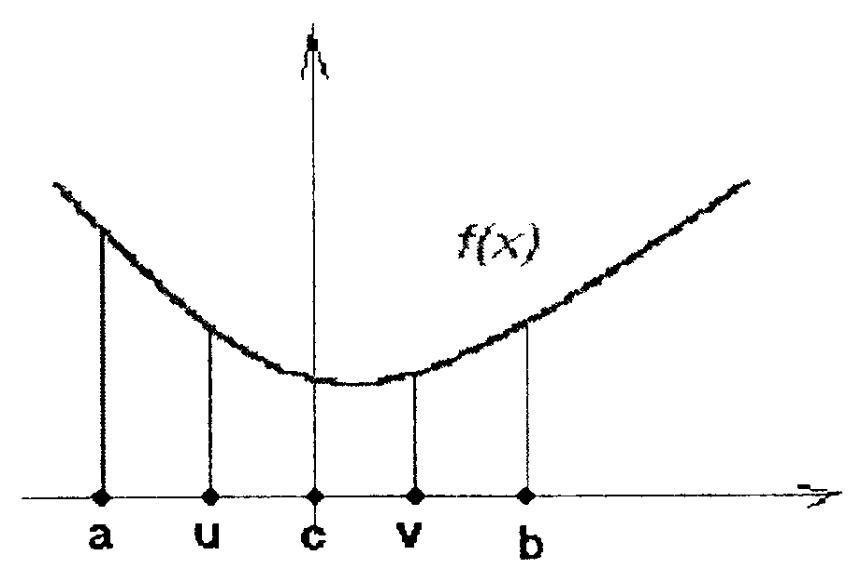
При применении данного ме­тода на каждом шаге рассматри­ваемый промежуток сокращается вдвое.

1)Разбиваем исходный отрезок [а,b] на 4 равные части и вычис­ляем значение функции в 5 точ­ках разбиения.

2)Ищем выпуклую тройку точек, минимум будет внутри. В слу­чае отсутствия выпуклой тройки берем половину с наименьшими значениями. Если полученный

отрезок больше, чем заданная точность, то переходим к п.1.

На каждом следующем шаге вычисляем по две новые точки. Таким обра­зом, на первом шаге вычислили значение функции 5 раз, а на каждом следую­щем вычисляем еще по два раза. Длина отрезка при каждом шаге сокращается ровно в 2 раза. Таким образом, чтобы отрезок сократился в 1024 раза требуется 23 вычисления функции.

Метод деления пополам №2

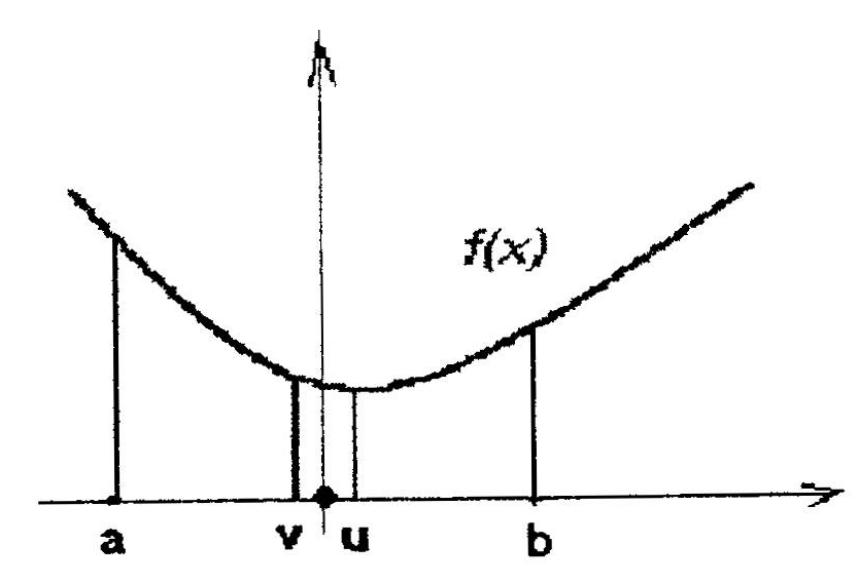Рассматривая отрезок [а,b], находим его середину. Далее отсту­паем влево и вправо на расстояние заранее заданной погрешности, получая точки v и u, затем вычисляем значения функции в этих точках.

Если

f(v)<f(u), то отрезок, на котором ищем минимум, сужаем до [а,u]; f(v)>f(u), то отрезок, на котором ищем минимум, сужаем до [v,b]; f(v)=f(u), что крайне маловероятно, то отрезок, на котором ищем минимум, сужаем до [v,u] .

Метод «золотого сечения»

Метод «золотого сечения» - метод одномерной оптимизации, в которой на каждом шаге поиска экстремума исследуется интервал управляемой перемен­ной X, разделенной на 3 подынтервала в соответствии с «золотым сечением» (рис. 6.10).

Результат шага - сужение интервала за счет отбрасывания, по крайней ме­ре, одного из крайних подынтервалов. Шаги повторяются, пока длина сужаю­щегося интервала не станет меньше заданной погрешности решения задачи.

Вычислим, чему равно отношение отрезков, на которые точка v делит отрезок [а, b] в «золотом сечении». «Золотое сечение» задается отношением:

Найдем, чему равно это отношение:

Для нахождения х получается квадратное уравнение:

Решение, которого дает значение отношения:

Утверждение: Если точки С и D делят [А,В] в "золотом сечении", то и С делит [A,D] в "золотом сечении" (рис. 6.11.).

Алгоритм

1. Вычисляем значение в точках С, D и если:

f(C)<f(D), то отрезок, на котором ищем минимум, сужаем до [A,D];

f(C)>f(D), то отрезок, на котором ищем минимум, сужаем до [С,В];

f(C)=f(D), что крайне маловероятно, то отрезок, на котором ищем минимум, сужаем до [С,В].

2. Добавляем еще одну точку, симметричную оставшейся C или D. Повторяем шаги 1-2, пока отрезок не станет меньше заранее заданной погрешности.

Метод Нелдера-Мида

Метод Нелдера-Мида, также известный как метод деформируемого многогранника, — метод безусловной оптимизации вещественной функции от нескольких переменных. Иными словами на допустимое множество накладываются следующие ограничения:

.

Кроме того, одним из главных преимуществ данного метода является то, что в нем не используется градиента целевой функции, что позволяет применять его к негладким функциям. Метод Нелдера-Мида использует понятие симплекса  -мерного пространства'.

Симплексом или  -симплексом называется выпуклая оболочка множества   точек.

Параметрами метода являются:

коэффициент отражения  , обычно выбирается равным 1.

коэффициент сжатия  , обычно выбирается равным 0.5.

коэффициент растяжения  , обычно выбирается равным 2.

Инициализация. Строится начальный симплекс.

1. Сортировка. Из вершин симплекса выбираем две точки:   с наибольшим (из выбранных) значением функции   и   с наименьшим значением функции  . Целью дальнейших манипуляций будет уменьшение по крайней мере  .

2. Найдём центр тяжести всех точек, за исключением  .

3. Отражение. Отразим точку   относительно   с коэффициентом   (при   это будет центральная симметрия, в общем случае — гомотетия), получим точку   и вычислим в ней функцию:  . Координаты новой точки вычисляются по формуле 

4. Далее сравниваем значение   со значениями : и

Если  , то производим растяжение. Новая точка   и значение функции  .

Если  , то заменяем точку   на   и заканчиваем итерацию (на шаг 8).

Если  , то заменяем точку   на   и заканчиваем итерацию (на шаг 8).

Если  , то переходим на шаг 5.

5. Сжатие. Строим точку   и вычисляем в ней значение  .

6. Если  , то заменяем точку   на   и переходим на шаг 8.

7. Если  , то производим сжатие симплекса (редукция) — гомотетию к точке с наименьшим значением  :  для всех требуемых точек  .

8. Последний шаг — проверка сходимости. Может выполняться по-разному, например, оценкой дисперсии набора точек. Суть проверки заключается в том, чтобы проверить взаимную близость полученных вершин симплекса, что предполагает и близость их к искомому минимуму. Если требуемая точность ещё не достигнута, можно продолжить итерации с шага 1.

Условная минимизация. Теорема Куна-Таккера.

Условная минимизация (оптимизация) или нелинейное программирование в узком смысле – рассматриваются методы нахождения минимумов (максимумов) функций многих переменных на множествах определяемых системой уравнений и неравенств.

Постановка задачи

Рассмотрим задачу нелинейной оптимизации. Пусть есть функции

при условиях .

Если при наложенных ограничениях — решение задачи, то найдётся ненулевой вектор множителей Лагранжа такой, что для функции Лагранжа выполняются условия:

стационарности — ;

дополняющей нежёсткости — ;

неотрицательности — .

[править]

Достаточные условия минимума функции

Перечисленные необходимые условия минимума функции в общем случае не являются достаточными. Существует несколько вариантов дополнительных условий, которые делают их достаточными.

Простая формулировка

Если для допустимой точки выполняются условия стационарности, дополняющей нежёсткости и неотрицательности, а также λ1 > 0, то .

Более слабые условия

Если для допустимой точки выполняются условия стационарности, дополняющей нежёсткости и неотрицательности, а также (условие Слейтера), то .

Цели и задачи исследования математических моделей систем. Этапы построения моделей. Этап построения концептуальной модели. Этап алгоритмизации и машинной реализации. Этап получения и интерпретации результатов.

Основные этапы построения моделей 1. Постановка цели моделирования 2. Анализ моделирования объекта и выделение всех его известных свойств 3. Анализ его выделенных свойств с точки зрения цели моделирования и определение, какие из них следует считать существенными 4. Выбор формы представления модели 5. Формализация 6. Анализ полученной модели на непротиворечивость 7. Анализ адекватности полученной модели объекты и цели моделирования.

Не существует универсальных правил определения, какие из известных свойств объекта являются существенными для конкретного случая. Если условия моделирования позволяют, то рекомендуется построить несколько моделей с разными наборами "существенных" свойств и затем оценить их на адекватность объекту и цели моделирования.

Цели моделирования Решение любой практической задачи всегда связано с исследованием, преобразованием некоторого объекта (материального или информационного) или управления им. Цель моделирования возникает, когда субъект моделирования решает поставленную перед ним задачу, и зависит как от решаемой задачи, так и от субъекта моделирования. То есть цель моделирования имеет двойственную природу: с одной стороны, она объективна, так как вытекает из задачи исследования, с другой - субъективна, поскольку исследователь всегда корректирует её в зависимости от опыта, интересов, мотивов деятельности. Для одного объекта один субъект может построить несколько моделей, если он решает разные задачи, приводящие к разным целям моделирования. Для одного объекта разные субъекты могут построить разные модели, даже если задача моделирования у них одна. Выбор вида модели и её построение зависят от знаний, опыта, предпочтений, личных интересов субъекта.

Этап построения концептуальной модели

Первым этапом машинного моделирования является построение кон­цептуальной модели М, системы S и ее формализация, т. е. основным назначением этого этапа является переход от содержательного опи­сания объекта к его математической модели. Наиболее ответственными и на­именее формализованными моментами в этой работе являются проведение границы между системой S и внешней средой Е, упроще­ние описания системы и построение сначала концептуальной, а за­тем формальной модели системы. Модель должна быть адекват­ной, иначе невозможно получить положительные результаты моде­лирования. Под адекватной моделью понимается модель, которая с определенной степе­нью приближения на уровне понимания моделируемой системы S разработчиком модели отражает процесс ее функционирования во внешней среде Е. Математическая модель представляет собой совокупность соотношений (например, уравне­ний, логических условий, операторов), определяющих характери­стики процесса функционирования системы S в зависимости от структуры системы, алгоритмов поведения, параметров системы, воздействий внешней среды Е, начальных условий и времени

Формализации процесса функционирования лю­бой системы S должно предшествовать изучение составляющих его явлений. Результатом является описание процесса, в котором изложены закономерности, характерные для исследуемого процесса, и постановкуаприкладной задачи. Содержательное описание является исходным материалом для последующих этапов формализации.

Последовательность построения концептуальной модели М, системы и ее формализации:

1. Постановка задачи машинного моделирования системы.

2. Анализ задачи моделирования системы.

3. Определение требований к исходной информации об объекте моделирования и организация ее сбора.

4. Выдвижение гипотез и принятие предположений.

5. Определение параметров и переменных модели.

6. Установление основного содержания модели.

7. Обоснование критериев оценки эффективности системы.

8. Определение процедур аппроксимации;

9. Описание концептуальной модели системы.

10. Проверка достоверности концептуальной модели.

11. Составление технической документации по первому этапу.

Этап алгоритмизации и машинной реализации

Вторым этапом моделирования является этап алгоритмизации модели и ее машинная реализация. Этот этап представляет собой этап, направленный на реализацию идей и математических схем в виде машинной модели М процесса функционирования систем S.

Процесс функционирования системы S можно рассматривать как последовательную смену ее состояний в k-мерном пространстве. Задачей моделирования процесса функционирования исследуемой системы S является построение функций z, на основе которых можно провести вычисление интересующих характеристик процесса функционирования системы. Для этого необходимы соотношения, связывающие функции z с переменными, параметрами и временем, а также начальные условиями в момент времени t=t₀.

Существуют два типа состоя­ний системы:

1) особые, присущие процессу функционирования системы то­лько в некоторые моменты времени;

2) неособые, в которых процесс находится все остальное время. В этом случае функция состояния z_i(t) могут изменяться скачкообразно, а между особыми – плавно.

Моделирующие алгоритмы могут быть построены по «принципу особых состо­яний». Обозначим скачкообразное (релейное) изменение состояния z как z, а «принцип особых состояний» — как принцип z. «Принцип z» дает возможность для ряда систем существенно уменьшить затраты машинного времени на реализа­цию моделирующих алгоритмов.

Удобной фор­мой представления логической структуры моделей процессов функ­ционирования систем и машинных программ является схема. На различных этапах моделирования составляются следующие схемы моделирующих алгоритмов и программ:

Обобщенная (укрупненная) схема моделирующего алгоритма за­дает общий порядок действий при моделировании системы без каких-либо уточняющих деталей.

Детальная схема моделирующего алгоритма содержит уточне­ния, отсутствующие в обобщенной схеме.

Логическая схема моделирующего алгоритма представляет собой логическую структуру модели процесса функционирования систем S.

Схема программы отображает порядок программной реализа­ции моделирующего алгоритма с использованием конкретного ма­тематического обеспечения. Схема программы представляет собой интерпретацию логической схемы моделирующего алгоритма раз­работчиком программы на базе конкретного алгоритмического языка.

Этапы алгоритмизации модели и ее машинной реализации:

1. Построение логической схемы модели.

2. Получение математических соотношении.

3. Проверка достоверности модели системы.

4. Выбор инструментальных средств для моделирования.

5. Составление плана выполнения работ по программированию.

6. Спецификация и построение схемы программы.

7. Верификация и проверка достоверности схемы программы.

8. Проведение программирования модели.

9. Проверка достоверности программы.

10. Составление технической документации по второму этапу.

Получение и интерпретация результатов моделирования систем

На третьем этапе моделирования ЭВМ используется для проведения рабочих расчетов по составленной и отлаженной программе. Результаты этих расчетов позволяют проанализировать и сформулировать выводы о характеристиках процесса функционирования моделируемой системы S. В ходе машинного эксперимента изучается поведение исследуемой модели М процесса функционирования системы S на заданном интервале времени. Поэтому критерий оценки является в общем случае векторной случайной функцией, заданной на этом же интервале. Часто используют более простые критерии оценки, например вероятность определенного состояния системы в заданный момент времени, отсутствие отказов и сбоев в системе на интервале и т. д. При интерпретации результатов моделирования вычисляются различные статистические характеристики закона распределения критерия оценки. Прежде чем приступить к последнему, третьему, этапу моделирования системы, необходимо для его успешного проведения иметь четкий план действий, сводящийся к выполнению следующих основных подэтапов.

3.1. Планирование машинного эксперимента с моделью системы.

3.2.Определение требований к вычислительным средствам.

3.3.Проведение рабочих расчетов.

3.4.Анализ результатов моделирования системы.

3.5.Представление результатов моделирования.

3.6.Интерпретация результатов моделирования (переход от информации, полученной в результате машинного эксперимента с моделью к информации применительно к объекту моделирования).

3.7.Подведение итогов моделирования и выдача рекомендаций.

3.8.Составление технической документации по этому этапу. Эта документация должна включать в себя: а) план проведения машинного эксперимента; б) наборы исходных данных для моделирования; в) результаты моделирования системы; г) анализ и оценку результатов моделирования; д) выводы по полученным результатам моделирования; указание путей дальнейшего совершенствования машинной модели и возможных областей ее приложения.

Цели исследования модели: 1) Понять, как устроен конкретный объект, какова его структура, основные св-ва, з-ны развития и взаимодействия с окружающим миром 2) Научиться управлять объектом или процесом и определять наилучшие способы управления при заданных целях и критериях 3) Прогнозировать прямые и косвенные последвстияв реализации заданных воздействий на объект. Хорошо построенная модель дает новые знания об изучаемом объекте

Типовые математические схемы.

Типовые математические схемы и соответствующие им математический аппарат:

Дескриптивные статистические модели макроуровня – линейные и нелинейные алгебраические уравнения и системы.

Дескриптивные динамические модели макроуровня – обыкновенные диф.уравнения и системы.

Дескриптивные динамические модели микроуровня – уравнения в частных производных.

Оптимизационные модели – линейное программирование, нелинейное программирование.

Дискретные детерминированные и стохастические модели – теория автоматов.

Непрерывно-стохастические модели – системы массового обслуживания.

Сетевые модели – сети Петри.

Агрегативные модели – универсальны.