
- •Раздел 4
- •Теория электромагнитного поля
- •2.Общие вопросы
- •3.Краткие сведения из векторной алгебры
- •4.Первое уравнение Максвелла
- •5.Второе уравнение Максвелла
- •6.Третье уравнение Максвелла
- •8.Теорема Умова-Пойнтинга. Вектор Пойнтинга
- •9.Общая схема движения энергии в электрической цепи.
- •10.Электростатическое поле
- •11.Безвихревой характер электростатического поля
- •12.Электрический потенциал
- •13.Определение потенциала
- •14.Уравнение Пуассона и Лапласа
- •15.Г Рис. 5.11 раничные условия
- •16.Поле шарового электрода
- •17.Магнитное поле постоянных токов
- •18.Скалярный магнитный потенциал
- •19.Векторный магнитный потенциал
3.Краткие сведения из векторной алгебры
Пусть в области G пространства задана функция u =f (P) (P – любая точка области). Это означает, что в области G определено скалярное поле. Если G – область трехмерного пространства, то скалярное поле u можно рассматривать как функцию трех переменных x, y, и z (координат точки Р):
u = u (x, y, z). (5.10)
Пусть эта функция однозначна и имеет непрерывные частные производные первого порядка. При переходе из одной точки пространства к другой функция изменяется с некоторой скоростью. В каком-то направлении эта скорость будет максимальна, и называется градиентом функции. Градиент – величина векторная:
![]() ,
(5.11)
,
(5.11)
где i, j, k - единичные векторы (орты)
Итак, градиент есть вектор, направленный по нормали к поверхности уровня в сторону возрастания и численно равна скорости изменения функции по этому направлению.
 Для
сокращения записей в векторной алгебре
вводится понятие формального символического
вектора .– оператора Гамильтона ( -
набла):
Для
сокращения записей в векторной алгебре
вводится понятие формального символического
вектора .– оператора Гамильтона ( -
набла):
![]() .
(5.12)
.
(5.12)
В этом случае градиент трактуется как произведение оператора Гамильтона на скалярную функцию
![]() .
(5.13)
.
(5.13)
Рассмотрим
векторную функцию
![]() ,
заданную своими проекциями. Определим
скалярное произведение вектора
,
заданную своими проекциями. Определим
скалярное произведение вектора
![]() и
вектора
и
вектора
![]() :
:
![]() .
(5.14)
.
(5.14)
В результате получается скалярная функция – дивергенция вектора . Дивергенция характеризует расходимость или мощность источника.
Возьмем векторное произведение вектора и вектора При этом будем иметь в виду, что j x k = i , и i*i = 0 .

![]() .
(5.15)
.
(5.15)
 Получился
новый вектор, который характеризует
вращательную способность вектора F.
Рассмотрим одну координату ротора.
Первая составляющая (
Получился
новый вектор, который характеризует
вращательную способность вектора F.
Рассмотрим одну координату ротора.
Первая составляющая (![]() )
– есть скорость изменения координаты
Z самого вектора в
направлении орты j. В
этом направлении вектор растет, и как
бы закручивает мельницу против часовой
стрелки (рис. 5.1). Плоскость кручения
обозначается стрелкой, перпендикулярной
к плоскости, направленной к зрителю, и
в данном случае по направлению оси i.
Вторая составляющая – скорость изменения
координаты Y
самого вектора в направлении орты к.
Стрелка кручения так же направлена по
оси i. Остальные
координаты ротора получаются таким же
образом.
)
– есть скорость изменения координаты
Z самого вектора в
направлении орты j. В
этом направлении вектор растет, и как
бы закручивает мельницу против часовой
стрелки (рис. 5.1). Плоскость кручения
обозначается стрелкой, перпендикулярной
к плоскости, направленной к зрителю, и
в данном случае по направлению оси i.
Вторая составляющая – скорость изменения
координаты Y
самого вектора в направлении орты к.
Стрелка кручения так же направлена по
оси i. Остальные
координаты ротора получаются таким же
образом.
4.Первое уравнение Максвелла
Первое уравнение выводится на основе закона полного тока:
. (5.16)
Этот закон является основным законом, устанавливающим связь между магнитным полем и электрическим током. Он гласит: циркуляция вектора напряженности магнитного поля вдоль замкнутого контура равна алгебраической сумме токов, пронизывающих контур интегрирования. Графическая иллюстрация этого закона приведена на рис. 5.2. На этом рисунке изображен контур, расположенный в магнитном поле. Этот контур пронизывается током I. Для одной из точек контура изображен вектор напряженности магнитного поля H. Выделим бесконечно малый отрезок контура в окрестностях рассматриваемой точки и обозначим его вектором dl, проведенным по касательной к контуру. В пределах бесконечно малого отрезка dl вектор Н изменяется бесконечно мало. Подинтегральное выражение в законе полного тока представляет собой скалярное произведение векторов. Преобразуем левую часть уравнения по теореме Стокса:
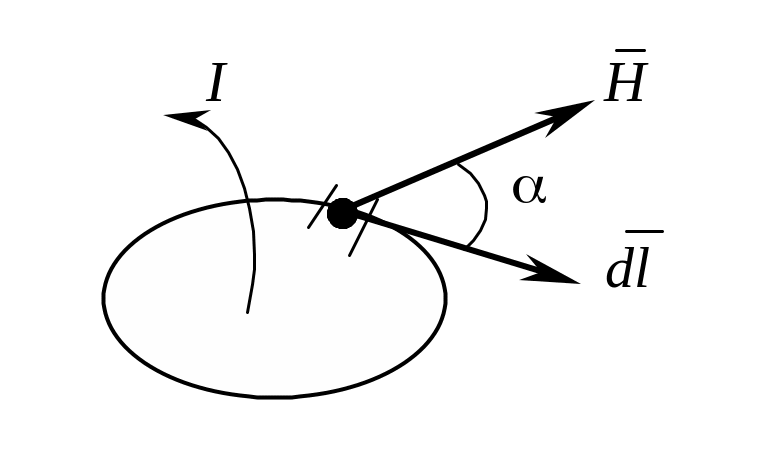 Рис.
5.2
Рис.
5.2![]() . (5.17)
. (5.17)
Правая часть полученного уравнения представляет собой поток ротора вектора напряженности магнитного поля сквозь поверхность, ограниченную контуром интегрирования. Правая часть закона полного тока может быть развернута следующим образом:
![]() .
(5.18)
.
(5.18)
Тогда закон полного тока запишется в виде
![]() .
(5.19)
.
(5.19)
Так как это равенство справедливо для всех значений интеграла, то подинтегральные функции равны между собой, т.е.
![]() .
(5.20)
.
(5.20)
Э то
есть первое уравнение Максвелла или
закон полного тока в дифференциальной
форме. Здесь δ =
δпр
+ δпер
+ δсм
- плотность
тока проводимости, плотность тока
переноса, и плотность тока смещения
соответственно.
Здесь δпр
= γЕ –
плотность тока проводимости,
δпер
– плотность тока переноса,
δсм
= dD/dt
– плотность
тока смещения. Ток проводимости и ток
переноса не могут существовать в одной
точке одновременно. Поэтому остается
δ
= δпр
+ δсм
. Тогда первое уравнение Максвелла
примет окончательный вид:
то
есть первое уравнение Максвелла или
закон полного тока в дифференциальной
форме. Здесь δ =
δпр
+ δпер
+ δсм
- плотность
тока проводимости, плотность тока
переноса, и плотность тока смещения
соответственно.
Здесь δпр
= γЕ –
плотность тока проводимости,
δпер
– плотность тока переноса,
δсм
= dD/dt
– плотность
тока смещения. Ток проводимости и ток
переноса не могут существовать в одной
точке одновременно. Поэтому остается
δ
= δпр
+ δсм
. Тогда первое уравнение Максвелла
примет окончательный вид:
![]() .
(5.21)
.
(5.21)
Это дифференциальное уравнение в частных производных, связывающее скорость изменения магнитного поля в пространстве (слева пространственные координаты) со скоростью изменения электрического поля во времени. Оно имеет, как и все дифференциальные уравнения, бесчисленное множество решений. Нужное решение может быть найдено с учетом начальных и граничных условий.
