
- •Билет № 1
- •1. Теоремы о взаимосвязи опорных решений задачи линейного программирования и угловых точек области допустимых решений.
- •Билет № 3
- •1. Необходимые и достаточные условия разрешимости транспортной задачи.
- •Билет № 4
- •1. Свойство системы ограничений транспортной задачи. Взаимосвязь линейной зависимости векторов-условий и циклов.
- •Билет № 5
- •1. Методы построения опорного решения транспортной задачи. Метод вычёркивания.
- •Билет № 6
- •Билет № 8
- •2. Теорема об единичном базисе.
- •Билет № 9
- •2. Теорема о двух линейно независимых системах векторов.
- •Билет № 10
- •2. Теорема о двух системах векторов, которым соответствуют равносильные системы уравнений.
- •Билет № 12
- •2. Общая теория систем уравнений. Теорема Кронекера-Капелли.
- •Билет № 13
- •2. Фундаментальная система решений однородной системы уравнений, теорема о её существовании.
- •Билет № 14
- •2. Необходимые и достаточные условия существования обратной матрицы.
- •Билет № 15
- •1. Построение начального опорного решения и переход от одного опорного решения к другому в симплексном методе (вывод формул).
- •Билет № 16
- •Теорема об улучшении опорного решения, её следствия.
- •Билет № 17
- •1. Теоремы о взаимосвязи опорных решений и угловых точек области допустимых решений.
- •Билет № 18
- •1. Метод искусственного базиса решения задач линейного программирования, его обоснование. Леммы и теорема об оптимальности опорного решения.
- •Билет № 20
- •Обоснование метод искусственного базиса решения задач линейного программирования. Теорема об отсутствии оптимального решения ввиду неограниченности целевой функции.
- •Билет № 21
- •1. Первая теорема двойственности, её доказательство.
- •Билет № 22
- •Вторая теорема двойственности, её доказательство.
- •Билет № 29
- •1. Теорема о виде области допустимых решений задачи линейного программирования.
- •Билет № 30
- •1. Теорема об улучшении опорного решения, её следствия.
Билет № 4
1. Свойство системы ограничений транспортной задачи. Взаимосвязь линейной зависимости векторов-условий и циклов.
Теорема 6.2. Ранг системы векторов-условий
транспортной задачи равен
![]() .
.
Д о к а з а т е л ь с т в о. Как известно из
линейной алгебры, для нахождения базиса
системы векторов
![]() необходимо составить однородную систему
уравнений
необходимо составить однородную систему
уравнений
![]() .
.
Эту систему с помощью преобразований Жордана приводят к равносильной разрешённой; в базис включают векторы, соответствующие разрешённым неизвестным. Ранг системы векторов равен числу векторов, входящих в базис, т. е. числу разрешённых неизвестных этой системы.
Системе векторов условий транспортной
задачи
![]() ,
i=1, 2, ..., m;
j = 1, 2, ..., n
соответствует однородная система
уравнений
,
i=1, 2, ..., m;
j = 1, 2, ..., n
соответствует однородная система
уравнений
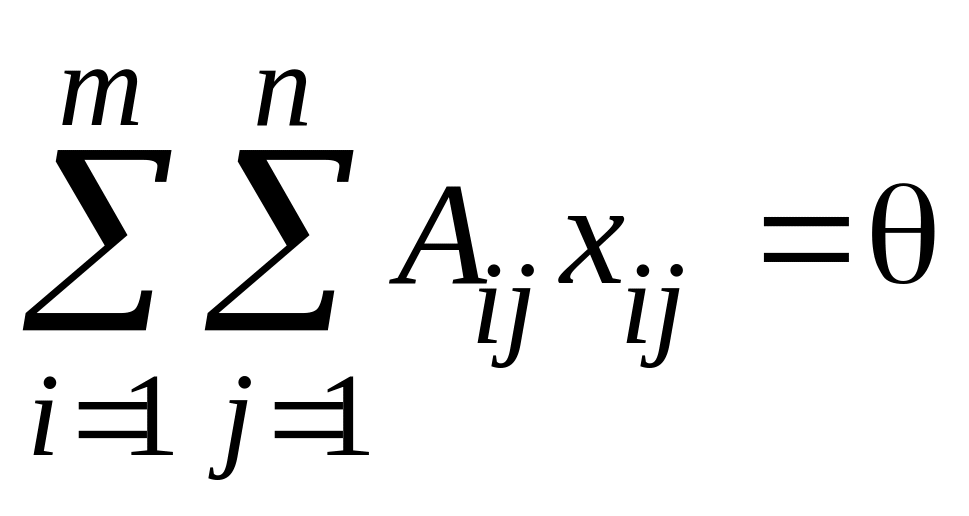 ,
где
,
где
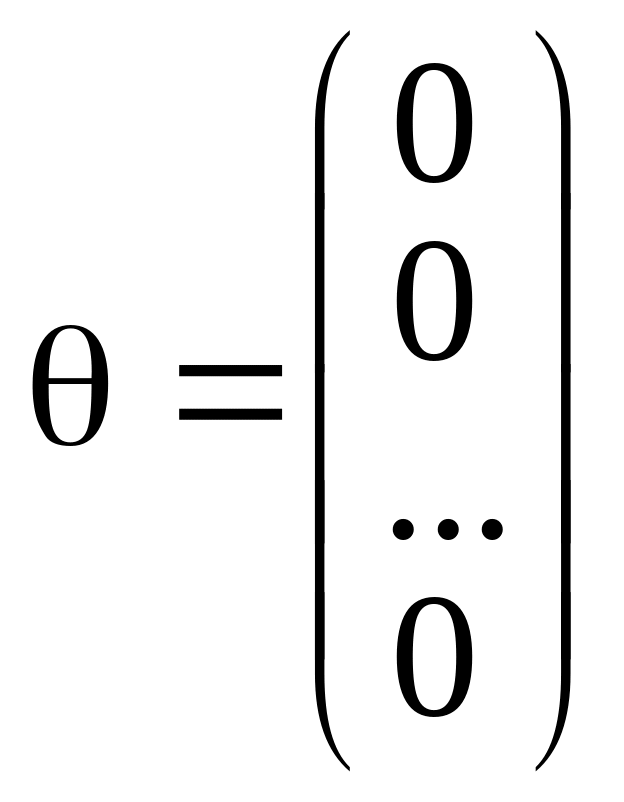 нулевой вектор.
нулевой вектор.
Запишем матрицу этой системы (она является также матрицей системы ограничений транспортной задачи):
|
|
|
... |
|
|
|
... |
|
... |
|
|
... |
|
|
1 |
1 |
... |
1 |
0 |
0 |
... |
0 |
... |
0 |
0 |
... |
0 |
m
mm m |
0 |
0 |
... |
0 |
1 |
1 |
... |
1 |
... |
0 |
0 |
... |
0 |
|
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
|
0 |
0 |
... |
0 |
0 |
0 |
... |
0 |
... |
1 |
1 |
... |
1 |
n |
1 |
0 |
... |
0 |
1 |
0 |
... |
0 |
... |
1 |
0 |
... |
0 |
|
0 |
1 |
... |
0 |
0 |
1 |
... |
0 |
... |
0 |
1 |
... |
0 |
|
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
|
0 |
0 |
... |
1 |
0 |
0 |
... |
1 |
... |
0 |
0 |
... |
1 |
Если к последней строке (уравнению) прибавить (n–1) строку (уравнений), начиная с (m + 1)-й, и вычесть первые m строк, то получится строка, состоящая из нулей. Это значит, что число разрешенных неизвестных в этой системе и ранг r системы векторов условий не может быть равен числу m + n. Следовательно, r m + n 1.
Покажем, что найдутся N
= m + n
1 линейно
независимых векторов условий. Из
векторов-условий задачи выберем
следующие:
![]() и убедимся, что они линейно независимые.
Для этого составим систему уравнений
и убедимся, что они линейно независимые.
Для этого составим систему уравнений
![]() .
.
Матрица этой системы имеет вид:
+
(1)
(1) + |
|
|
... |
|
|
|
... |
|
|
1 |
0 |
... |
0 |
1 |
1 |
... |
1 |
m mm m |
0 |
1 |
... |
0 |
0 |
0 |
... |
0 |
|
... |
... |
... |
... |
... |
... |
... |
... |
|
0 |
0 |
... |
1 |
0 |
0 |
... |
0 |
|
0 |
0 |
... |
0 |
1 |
0 |
... |
0 |
|
0 |
0 |
... |
0 |
0 |
1 |
... |
0 |
|
... |
... |
... |
... |
... |
... |
... |
... |
n |
0 |
0 |
... |
0 |
0 |
0 |
... |
1 |
|
1 |
1 |
... |
1 |
0 |
0 |
... |
0 |
C помощью элементарных
преобразований можно привести ее к
единичной. Для этого строки, с (m+1)-й
до (m+n1)-й
умножим на (1) и
прибавим к первой строке, тогда в ней
останется только одна единица, остальные
элементы будут нулевыми. После этого
первые m строк умножим
на (1) и прибавим к
последней строке. В результате в матрице
останутся единицы только по диагонали,
а последняя строка будет состоять из
нулей. Следовательно, эта система
уравнений имеет единственное нулевое
решение
![]() ,
а система векторов линейно независима.
,
а система векторов линейно независима.
Теорема 6.3 (о взаимосвязи линейной зависимости векторов условий и возможности образования цикла). Для того чтобы система векторов-условий транспортной задачи была линейно зависимой, необходимо и достаточно, чтобы из соответствующих им клеток таблицы можно было выделить часть, которая образует цикл.
Д о к а з а т е л ь с т в о. Необходимость. Пусть система, состоящая из n векторов
![]()
линейно зависима. Тогда существует
такой ненулевой набор чисел
![]() ,
что справедливо равенство
,
что справедливо равенство
![]() .
(6.10)
.
(6.10)
Пусть
![]() .
Вектор
.
Вектор
![]() имеет
только две равные единице координаты
с номерами
имеет
только две равные единице координаты
с номерами
![]() и
и
![]() ,
остальные равны нулю. В равенство
(6.10) должен входить ещё вектор, у
которого одна из этих координат равна
единице и который должен умножаться
на коэффициент
,
остальные равны нулю. В равенство
(6.10) должен входить ещё вектор, у
которого одна из этих координат равна
единице и который должен умножаться
на коэффициент
![]() ,
чтобы обеспечить равенство нулю этой
координаты в линейной комбинации
векторов. Пусть таким является вектор
,
чтобы обеспечить равенство нулю этой
координаты в линейной комбинации
векторов. Пусть таким является вектор
![]() .
Но этот вектор имеет кроме того
координату с номером
.
Но этот вектор имеет кроме того
координату с номером
![]() ,
равную единице. Следовательно, в равенство
(6.10) должен также входить вектор с
такой же единичной координатой и
т.д. В выбранной таким образом
последовательности векторов должен
найтись вектор
,
равную единице. Следовательно, в равенство
(6.10) должен также входить вектор с
такой же единичной координатой и
т.д. В выбранной таким образом
последовательности векторов должен
найтись вектор
![]() ,
у которого второй индекс совпадает
со вторым индексом первого вектора.
Данной последовательности векторов
соответствует совокупность клеток
таблицы транспортной задачи
,
у которого второй индекс совпадает
со вторым индексом первого вектора.
Данной последовательности векторов
соответствует совокупность клеток
таблицы транспортной задачи
(![]() ),
(
),
(![]() ),
(
),
(![]() ),
…, (
),
…, (![]() ),
),
которая образует цикл.
Достаточность. Пусть из соответствующих
векторам
![]() клеток (i, j)
выбрана последовательность клеток,
образующих цикл (
),
(
),
(
),
…, (
).
Нетрудно видеть, что
клеток (i, j)
выбрана последовательность клеток,
образующих цикл (
),
(
),
(
),
…, (
).
Нетрудно видеть, что
![]() .
.
Отсюда следует линейная зависимость рассматриваемой системы векторов.
Следствие. Допустимое решение
транспортной задачи
![]() i = 1, 2, ... , m;
j = 1, 2, ..., n
является опорным тогда и только
тогда, когда из занятых им клеток
таблицы нельзя образовать ни одного
цикла.
i = 1, 2, ... , m;
j = 1, 2, ..., n
является опорным тогда и только
тогда, когда из занятых им клеток
таблицы нельзя образовать ни одного
цикла.









