Билет № 12

2. Общая теория систем уравнений. Теорема Кронекера-Капелли.

Теорема 4.1. Теорема КронекераКапелли о совместности системы уравнений.

Для того, чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг расширенной матрицы системы r( ) равнялся рангу матрицы системы r(A), т. е. r( ) = r(A).

Данное условие считается более удобным, чем способ определения совместности системы, используемый в методе ЖорданаГаусса.

Д о к а з а т е л ь с т в о

Необходимость. Пусть система уравнений

совместна. Покажем, что r( ) = r(A).

Пусть система имеет некоторое частное решение К = ( ), т. е.

. Это равенство можно рассматривать как

разложение вектора В по векторам . Пусть r(A) = r и векторы образуют базис системы . Тогда любой из векторов

(j = 1, 2, …, n) разлагается по этому базису. Вектор B разлагается по векторам . Следовательно, он разлагается и по векторам . Любая максимальная линейно независимая подсистема векторов является базисом системы векторов. В системе подсистема является максимальной линейно независимой подсистемой, так как B разлагается по ней. Следовательно, r( ) = r(A).

Достаточность. Пусть r(A) = r( ) = r. Докажем, что в этом случае система уравнений совместна. Пусть базис системы векторов образуют векторы . Так как r( ) = r, то любая подсистема, состоящая из r линейно независимых векторов является ее базисом (см. теорему 3.6). Такой подсистемой для системы является . Следовательно, вектор В разлагается по векторам , .

Это соотношение можно дополнить равными нулю слагаемыми, не нарушая равенства, и записать в виде

.

Данное соотношение является подтверждением того, что система уравнений

имеет решение К = ( ), т. е. она совместна.

Билет № 13

2. Фундаментальная система решений однородной системы уравнений, теорема о её существовании.

Теорема 4.2. Если ранг матрицы системы однородных уравнений r меньше числа неизвестных n, то система уравнений имеет фундаментальную систему решений, состоящую из n  r векторов-решений.

Д о к а з а т е л ь с т в о. Пусть система записана в виде

.

Если ранг матрицы системы равен r (r(A) = r), то равносильная разрешенная система уравнений содержит r уравнений и имеет вид

.

Так как n > r, то система имеет n – r свободных неизвестных .

Задав свободным неизвестным значения 0 и 1, можно найти n – r частных решений вида

, , …, .

В этих векторах вместо значений базисных переменных поставлены точки, так как они в данном рассмотрении не имеют значения.

Покажем, что образуют фундаментальную систему решений. Чтобы доказать, что данные векторы являются линейно независимыми, составим линейную комбинацию

.

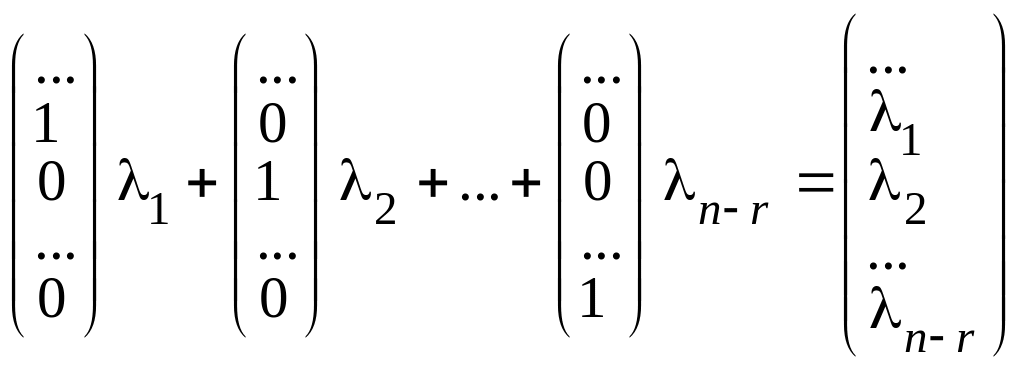Данная линейная комбинация равна нулевому вектору только при . Это и подтверждает линейную независимость векторов.

Покажем, что любое решение системы уравнений является линейной комбинацией .

Составим вектор К, являющийся линейной комбинацией векторов с коэффициентами

.

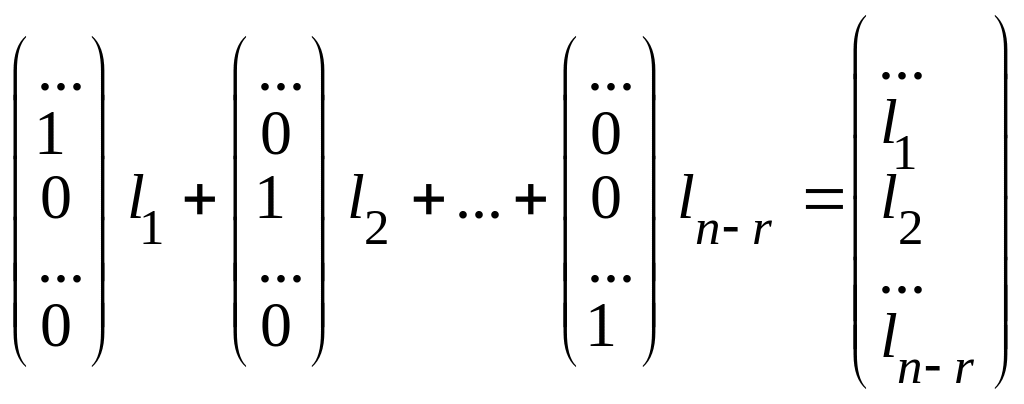Решения L и K при одних и тех же разрешенных неизвестных имеют одинаковые свободные неизвестные, следовательно, они совпадают (L = K), т. е.

.