Билет № 16
Теорема об улучшении опорного решения, её следствия.
Преобразование целевой функции при переходе от одного опорного решения к другому.
Пусть имеется опорное решение
задачи линейного программирования
(4.1)(4.3)
c базисом
.
Значение целевой функции задачи на
этом решении равно
.
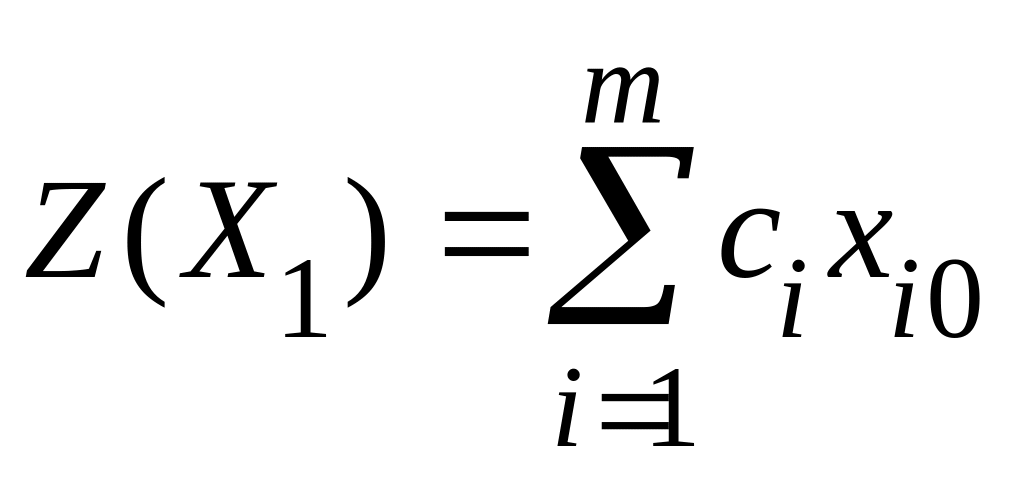Используя преобразование Жордана с
разрешающим элементом
,
перейдём к другому опорному решению
с базисом
,
т.е. введём в базис вектор
и исключим вектор
.
Значение целевой функции на этом решении
.
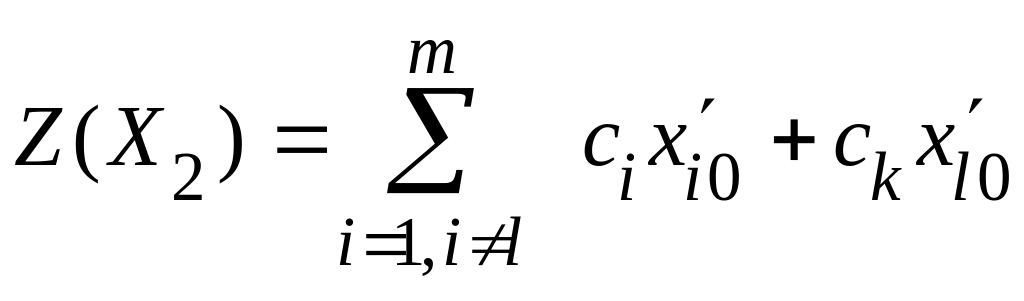Формулы пересчёта правых частей уравнений системы при преобразовании Жордана имеют вид
;
;
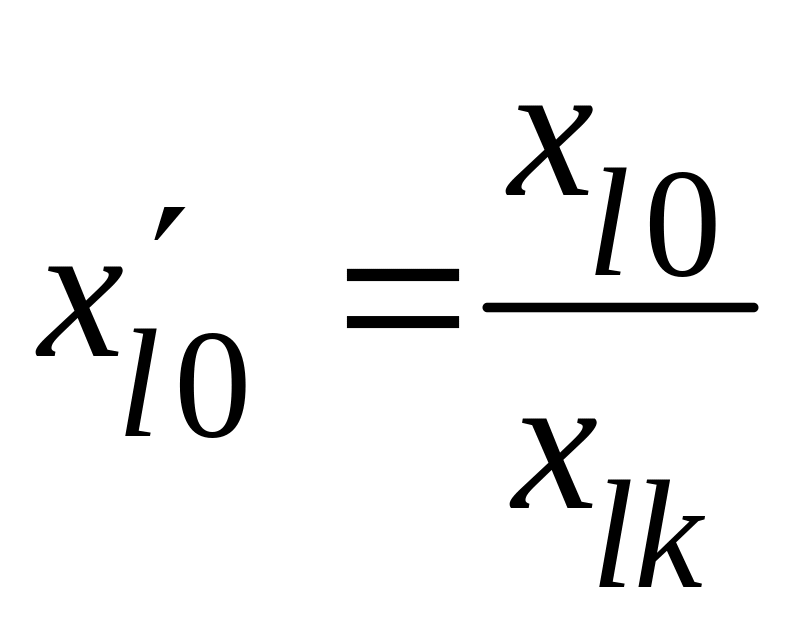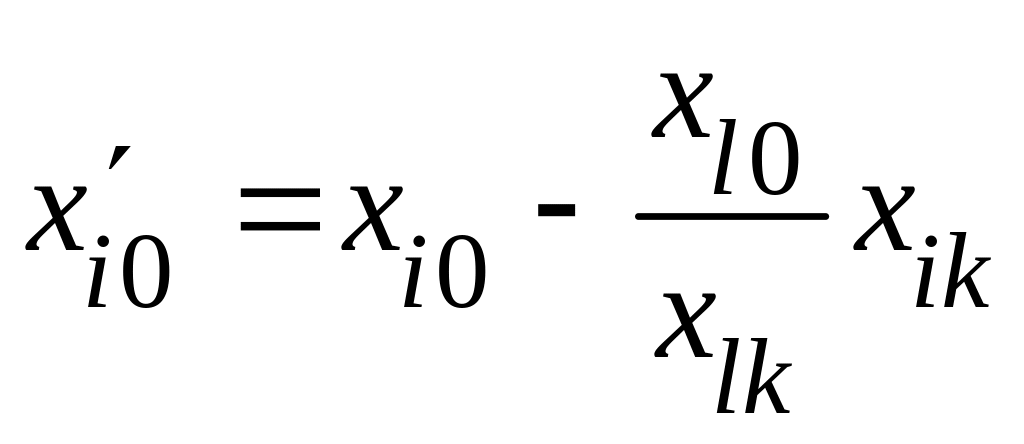i
= 1, 2, …, m;
i
l.
Используя эти формулы, получим
,
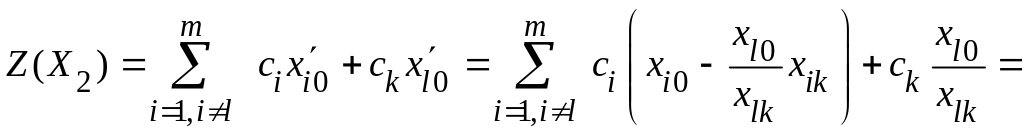
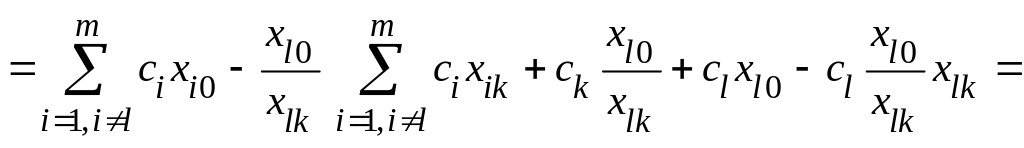
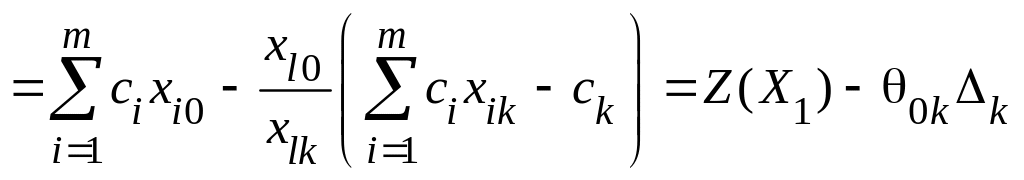т.е.
.
(4.6)
Отсюда находим приращение целевой функции при переходе от одного опорного решения к другому
.
(4.7)
Здесь через
обозначена величина, называемая оценкой
разложения вектора условий
по
базису опорного решения и
вычисляемая по формуле
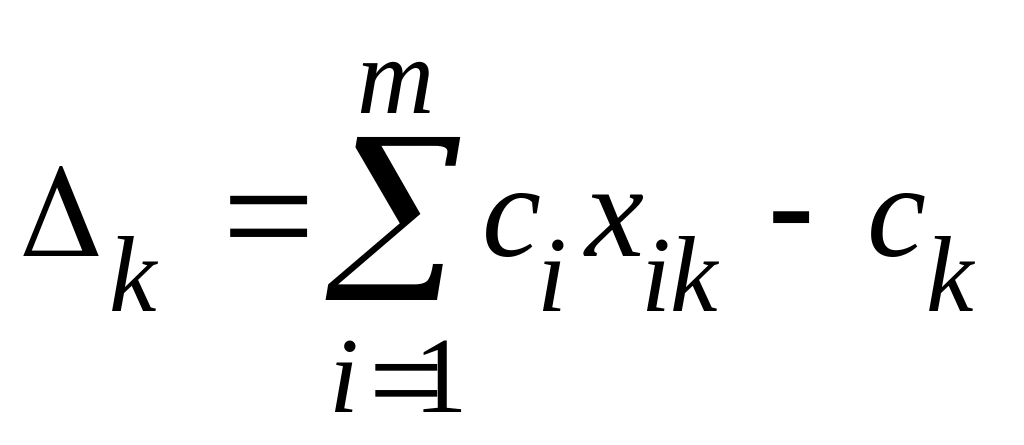(4.8)
или в векторной записи
,
(4.9)
где
вектор коэффициентов
целевой функции при базисных переменных,
вектор коэффициентов
разложения вектора
по базису опорного решения,
коэффициент целевой
функции при переменной
.
Теорема 4.1. Если в задаче линейного программирования на максимум (минимум) хотя бы для одного вектора условий оценка разложения по базису невырожденного опорного решения отрицательная (положительная), то опорное решение может быть улучшено, т.е. можно найти новое опорное решение, на котором значение целевой функции будет больше (меньше).
Д о к а з а т е л ь с т в о. Пусть решается
задача на максимум, которая имеет
невырожденное опорное решение
,
,
и оценка разложения некоторого вектора
условий
отрицательная (
).
Перейдем к новому опорному решению
,
введём в базис вектор
и исключим из базиса вектор
.
В этом случае приращение целевой
функции
.
Решение
невырожденное, поэтому параметр
,
вычисляемый по формуле (4.5), отличен
от нуля (
> 0). Так как
> 0,
,
то
.
Следовательно, значение целевой функции на новом опорном решении будет больше, чем на первом .
Доказательство для задачи на минимум аналогично.
Следствие 1 (условие наибольшего приближения к оптимальному решению). Для наибольшего изменения целевой функции при улучшении опорного решения необходимо выбор вектора выводимый из базиса (с номером l) и вводимого в базис (с номером k) производить из условий:
– в задаче на максимум
;
(4.10)
– в задаче на минимум
.
(4.11)
В упрощенном варианте выбор вектора, вводимого в базис, можно производить с использованием условий:
– в задаче на максимум
;
(4.12)
– в задаче на минимум
.
(4.13)
Этот вариант перехода к новому опорному решению обычно используется при расчетах на ЭВМ.
Следствие 2 (признак оптимальности опорного решения). Опорное решение задачи линейного программирования на максимум (минимум) является оптимальным, если для любого вектора условий оценка разложения по базису опорного решения неотрицательная (неположительная), т.е.
– в задаче на максимум
;
(4.14)
– в задаче на минимум
.
(4.15)
Действительно, если Z(x)
,
,
,
то
,
т.е. – оптимальное решение. Для задачи на минимум доказательство аналогично.
Следствие 3 (признак единственности оптимального решения). Оптимальное решение задачи линейного программирования является единственным, если для любого вектора условий, не входящего в базис, оценка отлична от нуля, т.е.
– в задаче на максимум
;
(4.16)
– в задаче на минимум
.
(4.17)
Здесь предполагается, что в базис оптимального решения входят первые m векторов.
Следствие 4 (признак существования бесконечного множества оптимальных решений). Задача линейного программирования имеет бесконечное множество оптимальных решений, если она имеет оптимальное решение, при котором хотя бы один из векторов условий, не входящих в базис оптимального решения, имеет оценку равную нулю, т.е.
k
{m+1, m+2,
..., n}:
.
(4.18)
Следствие 5 (признак отсутствия оптимального решения ввиду неограниченности целевой функции). Задача линейного программирования не имеет решения ввиду неограниченности целевой функции, если для какого-либо из векторов условий с оценкой , противоречащей признаку оптимальности, среди коэффициентов разложения по базису опорного решения нет положительного, т.е.
– в задаче на максимум
и
;
(4.19)
– в задаче на минимум
и
.
(4.20)