
- •Вопрос 6. Сложение гармонических колебаний.
- •Вопрос 7.Эффект Доплера для звуковых волн.
- •Вопрос 8. Волны. Энергия упругих волн. Вектор Умова.
- •Вопрос 9.Неинерциальные системы отсчета. Сила кориолиса
- •11. Закон сохранения энергии. Внутренняя энергия.
- •14. Центр инерции. Задача о движении 2ух тел.
- •21. Момент импульса. Его сохранение.
- •22. Связь законов сохранения с однородностью и изотропией пр-ва
- •23. Движение в центральном поле
- •24. Постулаты теории относительности. Преобразование Лоренца.
- •25. Следствия сто. Сокращение длин.
- •26. Сложение скоростей (релятивистское).
- •27. Дисперсия и групповая скорость волн.
- •30. Движение твердого тела. Расчет кинетической энергии.
- •Момент инерции твердого тела.
- •Скорость движения шара вниз по наклонной плоскости. (????????) (не знаю, то ли это, что надо)
- •Гармонические колебания и их свойства
- •Энергия гармонических колебаний
- •Уравнение гармонических колебаний и его решение
- •36. Периоды колебаний физического и математического маятников
- •38. Приведенная длинна физического маятника
- •39.Затухающие колебания. Решение уравнения
- •41.Резонанс при вынужденных колебаниях. Биения.
- •43/Параметрический.Резонанс
- •44/Предмет и методы молекулярной физики.
- •45/Идеальный газ и его законы.
- •56. Работа при изопроцессах.
- •57. Адиабатический процесс.
- •Внутренняя энергия идеального
- •Частные случаи первого закона термодинамики для изопроцессов
- •59. Процесс Джоуля-Томсона
- •60. Необратимость тепловых процессов. 2-й законн термодинамики
Скорость движения шара вниз по наклонной плоскости. (????????) (не знаю, то ли это, что надо)
Поскольку
сила трения работы не совершает, полная
энергия шара остается постоянной. В
начальный момент времени кинетическая
энергия равна нулю, потенциальная равна
mgh.
В конце скатывания потенциальная
энергия становится равной нулю, зато
появляется кинетическая энергия, равная
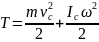 .
Т.к. скольжение отсутствует,
.
Т.к. скольжение отсутствует,
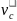 и
связаны соотношением
и
связаны соотношением
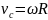 .
Подставив в выражение для кинетической
энергии
.
Подставив в выражение для кинетической
энергии
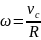 и
и
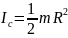 ,
получим:
,
получим:
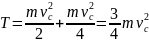 .
Полная энергия в начале и в конце
скатывания должна быть одинакова:
.
Полная энергия в начале и в конце
скатывания должна быть одинакова:
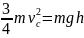 ,
откуда
,
откуда
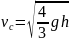 ,
а угловая скорость:
,
а угловая скорость:
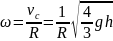
Гармонические колебания и их свойства
Колебания – процессы, хар-ся той или иной степенью повторяемости по времени. В зависимости от физ. природы повторяющегося процесса различают колебания: мех., эл-магн., эл-мех. и др..
Гармон
колеб-я – по закону sin/cos.
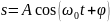 (A
– амплитуда, w0
–
цикл частота,
– нач фаза). Функция косинуса имеет
период
(A
– амплитуда, w0
–
цикл частота,
– нач фаза). Функция косинуса имеет
период
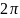 .
Значит, состояние колеблющегося тела
повторяется при изменении фазы на
.
.
Значит, состояние колеблющегося тела
повторяется при изменении фазы на
.
Состояния
системы повторяются через время T
– период.
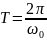 .
Частота:
.
Частота:
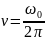
Диф
ур-е гармон колеб-ий:
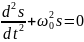 ;
;
Гармон колебания рассматриваются: 1)природ колеб-я близки к гармон; 2)различ колеб процессы можно представить как сумма гармон колеб-ий.
Зная
начальное положение и скорость тела,
можно определить амплитуду и начальную
фазу:
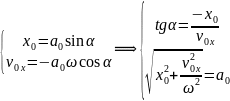
Энергия гармонических колебаний
Пусть
мат тчка совершает гармон колеб-я вдоль
оси oX
около положения равновесия, принятого
за начало координат, тогда:
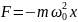 – сила, дейсвующая на колеб мат тчку.
– сила, дейсвующая на колеб мат тчку.
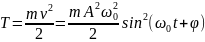 – кин.
энергия
– кин.
энергия
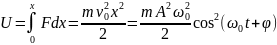 – потенц
энергия
– потенц
энергия
Кин
и потенц энергии зависят от времени.
Полная энергия (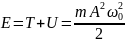 )
постоянна. T
и U
изменяются с частотой
)
постоянна. T
и U
изменяются с частотой
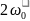 (в 2 раза больше, чем частота колеб-ий)
(в 2 раза больше, чем частота колеб-ий)
Уравнение гармонических колебаний и его решение
Из
2го закона Ньютона:
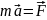 .
=>
.
=> ,
,
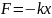 ).
=>
).
=>
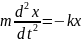 =>
=>
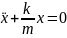 => (
=> (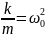 ).
Получаем
диф ур-ие, описывающее движение.
).
Получаем
диф ур-ие, описывающее движение.
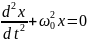
Решением дифференциального уравнения называется функция, обращающая это уравнение в тождество.
Нетрудно
проверить прямой подстановкой, что в
нашем случае решение имеет вид:

т.е. является гармонической функцией. Значит уравнение, это дифференциальное уравнение гармонических колебаний.
36. Периоды колебаний физического и математического маятников
Периодом
колебаний Т
называется наименьший промежуток
времени, за который система, совершающая
колебания, снова возвращается в то же
состояние, в котором она находилась
в начальный момент, выбранный произвольно.
При этом фаза получает приращение 2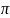 :
:
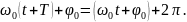 Отсюда
получается, что
Отсюда
получается, что
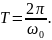 Математическим
маятником
называется идеализированная система,
состоящая из материальной точки
массой m,
подвешенной на нерастяжимой нити длиной
L
и колеблющейся под действием силы
тяжести без трения. Частота малых
колебаний зависит от длины маятника
Математическим
маятником
называется идеализированная система,
состоящая из материальной точки
массой m,
подвешенной на нерастяжимой нити длиной
L
и колеблющейся под действием силы
тяжести без трения. Частота малых
колебаний зависит от длины маятника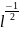 ,
но не
от массы тела. Формула для периода
колебаний математического маятника
называется
формулой Томсона.
Согласно период колебаний математического
маятника пропорционален его длине в
степени 1/2 . При
небольших углах отклонения
,
но не
от массы тела. Формула для периода
колебаний математического маятника
называется
формулой Томсона.
Согласно период колебаний математического
маятника пропорционален его длине в
степени 1/2 . При
небольших углах отклонения ![]() физический
маятник так же совершает гармонические
колебания. Будем считать, что вес
физического маятника приложен к его
центру тяжести в точке С. Силой, которая
возвращает маятник в положение
равновесия, в данном случае будет
составляющая силы тяжести – сила F.
физический
маятник так же совершает гармонические
колебания. Будем считать, что вес
физического маятника приложен к его
центру тяжести в точке С. Силой, которая
возвращает маятник в положение
равновесия, в данном случае будет
составляющая силы тяжести – сила F.
![]() Знак
минус в правой части означает то, что
сила F направлена в сторону уменьшения
угла α. С учетом малости угла
.
Так как угол маленький, у нас получается,
что F равно:
Знак
минус в правой части означает то, что
сила F направлена в сторону уменьшения
угла α. С учетом малости угла
.
Так как угол маленький, у нас получается,
что F равно:
![]() Для
вывода закона движения физического
маятников используем основное уравнение
динамики вращательного движения:
Для
вывода закона движения физического
маятников используем основное уравнение
динамики вращательного движения:
![]() Так
как момент силы определить в явном виде
нельзя. Надо записать дифференциальное
уравнение колебаний физического
маятника:
Так
как момент силы определить в явном виде
нельзя. Надо записать дифференциальное
уравнение колебаний физического
маятника:
![]() Сравнивая
полученное выражение с уравнением
гармонических колебаний:
Сравнивая
полученное выражение с уравнением
гармонических колебаний:
![]() Из
уравнения видно, что циклическая частота
пружинного маятника будет иметь
вид:
Из
уравнения видно, что циклическая частота
пружинного маятника будет иметь
вид:![]() Тогда
период колебаний математического
маятника будет равен:
Тогда
период колебаний математического
маятника будет равен:
![]()
![]() —
Период
физического маятника.
—
Период
физического маятника.
![]() —
Момент силы маятника относительно оси
вращения.
—
Момент силы маятника относительно оси
вращения.
![]() —
Расстояние от оси вращения до центра
масс.
—
Расстояние от оси вращения до центра
масс.
![]() —
Масса маятника.
—
Масса маятника.
![]() — Ускорение
свободного падения
— Ускорение
свободного падения
37.Если
известен момент инерции тела относительно
оси, проходящей через его центр масс,
то момент инерции относительно любой
другой параллельной оси определяется
теоремой Штейнера:
момент инерции тела I относительно
произвольной оси равен сумме момента
его инерции IС
относительно параллельной оси, проходящей
через центр масс тела, и произведения
массы
т
тела на квадрат
расстояния
а
между осями:![]()
Доказательство:
П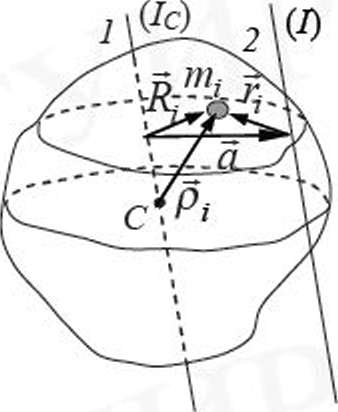 усть
усть
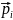 - радиус-вектор i-ro
элемента тела относительно центра
масс. Радиус-вектор центра масс системы
частиц относительно начала отсчета
выбранной системы отсчета равен
=
- радиус-вектор i-ro
элемента тела относительно центра
масс. Радиус-вектор центра масс системы
частиц относительно начала отсчета
выбранной системы отсчета равен
=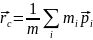 по
определению. В системе центра масс
по
определению. В системе центра масс
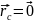 и, следовательно, относительно центра
масс суммарный вектор
и, следовательно, относительно центра
масс суммарный вектор
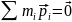 .Но
.Но
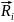 составляющая
вектора но
,
перпендикулярная осям 1 и 2. Следовательно,
если суммарный вектор равен нулю, то
сумма его составляющих в плоскости,
перпендикулярной осям 1 и 2, также равна
нулю.
составляющая
вектора но
,
перпендикулярная осям 1 и 2. Следовательно,
если суммарный вектор равен нулю, то
сумма его составляющих в плоскости,
перпендикулярной осям 1 и 2, также равна
нулю.
