
2. Бесконечная дифференцируемость аналитической функции
Теорема. Всякая функция f(z), аналитическая в области D, имеет производные всех порядков на этой области, и для z0D справедлива формула:
 , (7)
, (7)
где L – произвольный кусочно-гладкий замкнутый контур, целиком лежащий в D и содержащий внутри себя точку z0.
Замечание 1. Из (7) следует, что
 . (9)
. (9)
Замечание
2.
В теореме установлено, что если f(z)
имеет производную в любой
точке
z
из области D,
то она в каждой точке этой области имеет
производную любого порядка. Следовательно,
все производные аналитической функции
являются непрерывными. В частности,
если
f(z)
на D,
то она обязательно непрерывна. Для
действительной функции действительной
переменной это выполняется далеко не
всегда. Например,
 ,
,
 ,
f(x)
дифференцируема на
,
f(x)
дифференцируема на
 ,
,
 - не дифференцируема в точке x=0.
- не дифференцируема в точке x=0.
Вопрос №12. Теорема Морера
Согласно
теореме Коши если f(z)-аналитическая
на односвязной области D,
то она непрерывна на D
и для любого кусочно–гладкого замкнутого
контура LD
 .
Справедливо и обратное утверждение.
.
Справедливо и обратное утверждение.
Теорема (Морера). Если f(z) непрерывна в односвязной области D, и вдоль любого кусочно–гладкого замкнутого контура LD , то f(z) – аналитическая в D.
Доказательство.
Равенство
нулю интеграла
по любому кусочно–гладкому замкнутому
контуру LD
означает, что
 вдоль любой кривой, соединяющей точки
z0
и z
не зависит от вида кривой. Как было
доказано, функция
вдоль любой кривой, соединяющей точки
z0
и z
не зависит от вида кривой. Как было
доказано, функция
 является аналитической в D,
причём F(z)=f(z).
Но по предыдущей теореме f(z)-аналитическая
функция, так как является производной
аналитической функции.
является аналитической в D,
причём F(z)=f(z).
Но по предыдущей теореме f(z)-аналитическая
функция, так как является производной
аналитической функции.
Определение. Функция f(z) непрерывная на односвязной области D, называется аналитической на D, если по любому кусочно–гладкому замкнутому контуру LD.
Теорема о среднем
Теорема. Значение аналитической функции f(z) в центре круга равно среднему арифметическому её значений на окружности этого круга, то есть, если z-z0r круг, лежащий в области G, f(z)-аналитическая в G, то
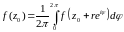 . (10)
. (10)
z=z0+rei, ([0,2])-уравнение окружности С с центром в точке z0, радиуса r.
По интегральной формуле Коши
 .
.
Принцип максимума модуля аналитической функции
Теорема. Модуль функции f(z),аналитической в некоторой области G и не равной тождественно константе, не может иметь максимума ни в одной точке этой области.
Доказательство.
Обозначим
 и предположим противное:
точка z0G:
f(z0)=M.
Из формулы (10) следует
и предположим противное:
точка z0G:
f(z0)=M.
Из формулы (10) следует
 . (11)
. (11)
Так
как
 ,
а f(z0)=M,
то из (11) следует, что
,
а f(z0)=M,
то из (11) следует, что
 .
.
Д ействительно,
если допустить, что при некотором
значении =0
ействительно,
если допустить, что при некотором
значении =0
 ,
то в силу непрерывности функции f(z)
неравенство
будет выполняться для любого
из
достаточно малого промежутка 0-0+,
а вне этого промежутка
.
Значит,
в этом случае правая часть неравенства
(11) должна быть меньше
M
,
то в силу непрерывности функции f(z)
неравенство
будет выполняться для любого
из
достаточно малого промежутка 0-0+,
а вне этого промежутка
.
Значит,
в этом случае правая часть неравенства
(11) должна быть меньше
M
 ,
а левая часть равна M
(f(z0)=M).
Этого быть не может. Следовательно, если
в некоторой точке z0
f(z0)=M,
то и в достаточно малой её окрестности
|z-z0|<r
.
,
а левая часть равна M
(f(z0)=M).
Этого быть не может. Следовательно, если
в некоторой точке z0
f(z0)=M,
то и в достаточно малой её окрестности
|z-z0|<r
.
П окажем
теперь, что f(z)=M
всюду в области G.
Пусть z1-
произвольная
точка области G.
Соединим точку z0
с точкой
z1
непрерывной линией L,
целиком лежащей в G.
Обозначим через d
расстояние от L
до границы области G.
Круг
с центром в произвольной точке кривой
L радиусом
окажем
теперь, что f(z)=M
всюду в области G.
Пусть z1-
произвольная
точка области G.
Соединим точку z0
с точкой
z1
непрерывной линией L,
целиком лежащей в G.
Обозначим через d
расстояние от L
до границы области G.
Круг
с центром в произвольной точке кривой
L радиусом
 принадлежит области G.
Следовательно, по доказанному f(z)=M
всюду внутри круга с центром в точке z0
радиуса
принадлежит области G.
Следовательно, по доказанному f(z)=M
всюду внутри круга с центром в точке z0
радиуса
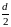 :
: .
Пусть центр этого круга непрерывно
перемещается по L
от точки z0
к точке
z1.
Равенство
f(z)=M
должно выполняться всё время внутри
круга, каково бы ни
было положение центра круга. Следовательно,
в частности f(z1)=M.
Так как z1
-
произвольная точка области G,
то это означает, что f(z)=M
всюду в области G.
.
Пусть центр этого круга непрерывно
перемещается по L
от точки z0
к точке
z1.
Равенство
f(z)=M
должно выполняться всё время внутри
круга, каково бы ни
было положение центра круга. Следовательно,
в частности f(z1)=M.
Так как z1
-
произвольная точка области G,
то это означает, что f(z)=M
всюду в области G.
Покажем теперь, что в этом случае f(z)const.
 -
аналитическая функция.
-
аналитическая функция.
 ,
следовательно, по условиям Коши-Римана
получим, что
,
следовательно, по условиям Коши-Римана
получим, что
 .
Следовательно, vconst.
Значит, и ln(f(z))const.
Поэтому f(z)const
в G.
.
Следовательно, vconst.
Значит, и ln(f(z))const.
Поэтому f(z)const
в G.
Получили противоречие с условием. Следовательно, предположение неверно, и аналитическая функция, не может иметь максимума модуля ни в одной точке области G.
Замечание.
Из
доказанного принципа следует, что если
f(z)-
аналитическая в области G
и
непрерывная в замкнутой области ,
то максимум модуля достигается на
границе области G
при
условии, что f(z)
,
то максимум модуля достигается на
границе области G
при
условии, что f(z) const.
В самом деле, так как f(z)-
непрерывная функция, то в замкнутой
области
она
принимает наибольшее значение в некоторой
точке z0
.Так
как точка z0
не может лежать в области
G
(по доказанной теореме), то она расположена
на границе области
G.
const.
В самом деле, так как f(z)-
непрерывная функция, то в замкнутой
области
она
принимает наибольшее значение в некоторой
точке z0
.Так
как точка z0
не может лежать в области
G
(по доказанной теореме), то она расположена
на границе области
G.
Вопрос №13. Степенные ряды в комплексной области. Коши-Адамар. Теорема Абеля.
Степенной ряд, радиус и круг сходимости
Определение.
Степенным рядом называется функциональный
ряд вида
 , (1)
, (1)
где an (n=0,1,2,…), zn - комплексные числа, z-комплексная переменная.
Числа an называются коэффициентами ряда, z0 - его центром.
Область определения степенного ряда - вся комплексная плоскость. Очевидно, что в точке z=z0 ряд (1) сходится. Следовательно, область сходимости любого степенного ряда состоит, по крайней мере, из одной точки.
Определение.
Число
 называется верхним пределом
последовательности действительных
чисел {n}:
называется верхним пределом
последовательности действительных
чисел {n}:
 ,
если выполнены условия:
,
если выполнены условия:

 ;
;cуществует подпоследовательность
 .
.
(Верхний предел - наибольший из частичных пределов; частичный предел- предел подпоследовательности.)
Теорема
(Коши-Адамара). Пусть дaн степенной ряд
(1) и
 .
Тогда
.
Тогда
при =0 ряд абсолютно сходится во всей комплексной плоскости,
при = (1) сходится только в точке z=z0 и расходится zz0,
если 0<<, то (1) абсолютно сходится в круге
 и расходится вне этого круга.
и расходится вне этого круга.
Доказательство.
1) Пусть =0.
Тогда
 .
Следовательно, z
выполнено
.
Следовательно, z
выполнено
 ,
значит, по признаку Коши ряд
,
значит, по признаку Коши ряд
 сходится.
Следовательно, ряд (1) сходится абсолютно
во всей комплексной плоскости.
сходится.
Следовательно, ряд (1) сходится абсолютно
во всей комплексной плоскости.
2) Пусть =.
Тогда существует подпоследовательность


 .
Следовательно, для (1) не выполняется
необходимое условие сходимости, поэтому
ряд расходитсяzz0.
.
Следовательно, для (1) не выполняется
необходимое условие сходимости, поэтому
ряд расходитсяzz0.
 3)
Пусть0<<.
Если z=z0,
то все члены ряда, начиная со второго,
равны нулю, и, следовательно, ряд абсолютно
сходится. Если zz0
и z
лежит внутри K,
то положим
3)
Пусть0<<.
Если z=z0,
то все члены ряда, начиная со второго,
равны нулю, и, следовательно, ряд абсолютно
сходится. Если zz0
и z
лежит внутри K,
то положим
 ,
где
,
где
 .
Обозначим
.
Обозначим
 .
Тогда по свойству 1) верхнего предела
.
Тогда по свойству 1) верхнего предела
 .
Отсюда
.
Отсюда
 .
Следовательно, по признаку Коши (1)
абсолютно сходится.
.
Следовательно, по признаку Коши (1)
абсолютно сходится.
Если
z
лежит вне круга К,
то положим
 .
По свойству 2) верхнего предела существует
подпоследовательность
.
По свойству 2) верхнего предела существует
подпоследовательность
 .
Следовательно,
.
Следовательно,
 .
Отсюда
.
Отсюда
 .
То
есть для ряда (1) не выполнено необходимое
условие сходимости, и ряд расходится.
.
То
есть для ряда (1) не выполнено необходимое
условие сходимости, и ряд расходится.
Определение.
Круг с центром z0
и радиусом
 ,
внутри которого степенной ряд сходится
абсолютно, а во внешности расходится,
называется кругом
сходимости степенного ряда,
а число
,
внутри которого степенной ряд сходится
абсолютно, а во внешности расходится,
называется кругом
сходимости степенного ряда,
а число
 -
радиусом
сходимости.
-
радиусом
сходимости.
Если =0 (R=), то круг сходимости – вся конечная комплексная плоскость.
Если = (R=0), то круг вырождается в точку z0, а в его внешности, т.е. во всей комплексной плоскости, кроме точки z0, ряд расходится.
Н а
окружности
а
окружности
 ряд (1) может вести себя по-разному: может
сходиться во всех точках окружности,
расходиться во всех точках, может в
одних сходиться, а в других расходиться.
ряд (1) может вести себя по-разному: может
сходиться во всех точках окружности,
расходиться во всех точках, может в
одних сходиться, а в других расходиться.
Из теоремы Коши-Адамара вытекает
Теорема
2 (Абеля).
Если ряд (1) сходится в точке z1z0,
то он абсолютно сходится в круге
 .
.
Доказательство.
Так как ряд сходится в точке z1, то она не может лежать вне круга сходимости, значит, она лежит внутри него или на границе. В обоих случаях круг принадлежит кругу сходимости, следовательно, в нем ряд сходится.
Замечание.
Степенной ряд равномерно сходится в
каждом замкнутом круге
 ,
лежащем внутри круга сходимости.
Действительно
,
лежащем внутри круга сходимости.
Действительно
 .
Т.к. r<R,
то числовой ряд
.
Т.к. r<R,
то числовой ряд
 сходится, следовательно, по признаку
Вейерштрасса степенной ряд сходится
равномерно в
.
сходится, следовательно, по признаку
Вейерштрасса степенной ряд сходится
равномерно в
.
Аналитичность суммы степенного ряда.
Теорема
3.
В круге сходимости |z-z0|<R
(R>0)
степенного ряда (1)
его сумма f(z)
является аналитической функцией, причем
 может быть получена путем почленного
дифференцирования ряда (1):
может быть получена путем почленного
дифференцирования ряда (1):
 . (2)
. (2)
Доказательство.
 Пусть
R–
радиус сходимости ряда (2). Покажем, что
R=R.
Очевидно, что R
совпадает
с радиусом сходимости ряда
Пусть
R–
радиус сходимости ряда (2). Покажем, что
R=R.
Очевидно, что R
совпадает
с радиусом сходимости ряда
 .
Тогда
.
Тогда
 .
.
Пусть
z1
принадлежит
кругу |z-z0|<R,
возьмем точку
 так, чтобы
так, чтобы
 .
Так как точка
принадлежит кругу сходимости, то ряд
.
Так как точка
принадлежит кругу сходимости, то ряд
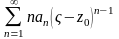 абсолютно
сходится и, следовательно,
абсолютно
сходится и, следовательно,
 выполнено
выполнено
 . (3)
. (3)
Положим
 .
Тогда если zz1,
|z-z0|
то оценим
.
Тогда если zz1,
|z-z0|
то оценим
 .
.
Используя равенство
 ,
,
получим





 Перейдем
к пределу при
Перейдем
к пределу при
 тогда
тогда
 .
Следовательно, для выбранного
()>0:
при |z-z1|<()
.
Следовательно, для выбранного
()>0:
при |z-z1|<()
 .
В
силу (3) rn<.
.
В
силу (3) rn<.
Следовательно,
 при |z-z1|<(),
отсюда
при |z-z1|<(),
отсюда
 .
.
Так как z1 - произвольная точка внутри круга сходимости, то отсюда следует, что сумма степенного ряда (1) является аналитической функцией, и ее производная
Вопрос №14. Теорема о единственности. Разложение аналитической функции в степенной ряд.
Разложение некоторых функций в ряд Тейлора:
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Ряд Тейлора
Теорема 4(о единственности). Если функция f(z) разлагается в степенной ряд (1) в круге |z-z0|<R, то это разложение единственно.
Доказательство.
По
условию
 в круге |z-z0|<R.
По теореме 3
в круге |z-z0|<R.
По теореме 3
 - аналитическая в круге |z-z0|<R
и к ней можно применить теорему 3 и т.д.
Получим
- аналитическая в круге |z-z0|<R
и к ней можно применить теорему 3 и т.д.
Получим




…………………………………………………………………………..

Положим z=z0. Тогда
 ,
,
 ,
,
………………..
 …
…
Подставляя
найденные коэффициенты в (1), получим
 . (4)
. (4)
Ряд (4) называется рядом Тейлора функции f(z).
Покажем единственность разложения.
Пусть
 и
и
 .
Тогда по доказанному
.
Тогда по доказанному
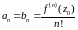 ,
следовательно, разложение единственно.
Т.е. если функция f(z)
разлагается в степенной ряд, то это
разложение единственно и является рядом
Тейлора.
,
следовательно, разложение единственно.
Т.е. если функция f(z)
разлагается в степенной ряд, то это
разложение единственно и является рядом
Тейлора.
Замечание. В процессе доказательства теоремы 4 установили, что сумма степенного ряда (1) бесконечно дифференцируема в круге сходимости |z-z0|<R; производная любого порядка m получается m- кратного почленного дифференцирования ряда (1).
Вопрос №15. Теорема о разложение аналитической функции в степенной ряд. Теорема Лиувилля.
Теорема 5. Пусть функция f(z)- однозначная и аналитическая в области G. Если z0G и r - расстояние от z0 до границы области G, то в круге |z-z0|<r f(z) разлагается в степенной ряд, расположенный по степеням (z-z0).
Доказательство.
 Возьмем
z{|z-z0|<r}.
Рассмотрим круг
Возьмем
z{|z-z0|<r}.
Рассмотрим круг
 .
.
 –его
граница
–его
граница
 .
.
Согласно интегральной формуле Коши
 .
.
Разложим
 в степенной ряд по степеням z-z0:
в степенной ряд по степеням z-z0:
 ;
;
Так
как
 ,
то
,
то
 является суммой членов бесконечной
геометрической прогрессии со знаменателем
является суммой членов бесконечной
геометрической прогрессии со знаменателем
 и
и
 .
Тогда
.
Тогда
 .
.
Отсюда
 . (5)
. (5)
Так как для каждого фиксированного z
 ,
,
и
числовой ряд

 сходится
как геометрическая прогрессия со
знаменателем
сходится
как геометрическая прогрессия со
знаменателем

 ,
то по признаку Вейерштрасса равномерной
сходимости ряд (5) абсолютно и равномерно
сходится относительно
,
то по признаку Вейерштрасса равномерной
сходимости ряд (5) абсолютно и равномерно
сходится относительно 
 и, следовательно, его можно интегрировать
почленно. Тогда
и, следовательно, его можно интегрировать
почленно. Тогда

 Получили
степенной ряд с коэффициентами:
Получили
степенной ряд с коэффициентами:
 . (6)
. (6)
Эти
коэффициенты не зависят от радиуса
 .
Действительно, если 1
и 0<1<r,
.
Действительно, если 1
и 0<1<r,
 то
по следствию из интегральной теоремы
Коши
то
по следствию из интегральной теоремы
Коши

 .
.
Итак,
мы показали, что f(z)
разлагается в степенной ряд  .
.
Так
как z
- произвольная точка круга |z-z0|<r,
то теорема доказана.

Из теоремы 5 следует еще одно определение аналитической функции.
Определение 1. Функция f(z) называется аналитической в точке z0, если она разлагается в степенной ряд в некоторой окрестности точки z0.
Определение 2. Функция f(z) называется аналитической на области D, если она разлагается в степенной ряд в некоторой окрестности каждой точки z0D.
Следствие.
Положим

 .
Из (6) следует следующая оценка коэффициентов
степенного ряда:
.
Из (6) следует следующая оценка коэффициентов
степенного ряда:
 ,
,

 -
неравенства
Коши,
-
неравенства
Коши,
(где 0<<r, |z-z0|<r - круг сходимости ряда (1)).
Эти неравенства позволяют оценить сверху модули коэффициентов степенного ряда через максимум модуля суммы ряда на окружности |z-z0|= и радиус этой окружности.
Из неравенств Коши следует теорема.
Теорема 6 (Лиувилля). Если f(z) – аналитическая на всей комплексной плоскости и ограничена по модулю на ней, то эта функция есть константа.
Доказательство.
 Так как f(z)
– аналитическая на всей комплексной
плоскости, то она разлагается в степенной
ряд с центром в точке z0=0:
Так как f(z)
– аналитическая на всей комплексной
плоскости, то она разлагается в степенной
ряд с центром в точке z0=0:
 .
.
Ряд
сходится во всей комплексной плоскости,
т.е. R=.
Так как f(z)
ограничена по модулю на
 ,
то M>0:
|f(z)|M,
тогда по неравенствам Коши:
,
то M>0:
|f(z)|M,
тогда по неравенствам Коши:
 ,
,
где
в качестве
можно взять любое положительное число.
Зафиксируем
 и
перейдем к пределу при .
Получим |an|0,
т.е. |an|=0
n=1,2,…
. Следовательно, f(z)a0=const,
и
перейдем к пределу при .
Получим |an|0,
т.е. |an|=0
n=1,2,…
. Следовательно, f(z)a0=const,
 и
теорема доказана.
и
теорема доказана. 
Вопрос №16. Теорема о единственности и нули аналитических функций
Теорема(единственности).
Если две функции f(z)
и g(z) ,
аналитические в некоторой области G,
имеют равные значения на бесконечном
множестве точек EG,
которое имеет по крайней мере одну
предельную точку, лежащую внутри G,
то f(z)=g(z)
всюду в G
(т.е. f(z)g(z)).
,
аналитические в некоторой области G,
имеют равные значения на бесконечном
множестве точек EG,
которое имеет по крайней мере одну
предельную точку, лежащую внутри G,
то f(z)=g(z)
всюду в G
(т.е. f(z)g(z)).
Доказательство.
 Пусть
z0
- предельная точка множества EG.
Пусть
z0
- предельная точка множества EG.
1) Пусть G – круг с центром в точке z0. Так как f(z) и g(z) - аналитические функции, то по теореме 5 §15 в любой точке z круга G имеют место разложения этих функций в степенной ряд:
 ,
,
 .
.
Достаточно доказать равенство коэффициентов an=bn n0. По условию, если zE,то f(z)=g(z). (*)
Так
как z0
- предельная точка множества Е,
то можно выделить последовательность
{zk}E:
 .
Так
как
f(zk)=g(zk)
.
Так
как
f(zk)=g(zk) ,
то переходя в этом равенстве к пределу
при k,
получим
f(z0)=g(z0)
a0=b0.
Тогда (*) примет вид:
,
то переходя в этом равенстве к пределу
при k,
получим
f(z0)=g(z0)
a0=b0.
Тогда (*) примет вид:
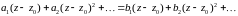 ,
,
где z- произвольная точка множества Е. Сокращая на z- z0, получим
 .
.
Это
равенство имеет место zE,
в частности, при z=zk,
где  .
Переходя к пределу, получим a1=b1.
Поступая и так далее найдем:
.
Переходя к пределу, получим a1=b1.
Поступая и так далее найдем:

 2,…
an=b
n
.
Следовательно, f(z)=g(z)
в G.
2,…
an=b
n
.
Следовательно, f(z)=g(z)
в G.
2
z’


d
 )
Пусть G
– произвольная область, f(z)=g(z)
на бесконечном множестве EG
и Е
имеет предельную точку z0G.
Пусть z
- произвольная точка области G.
Покажем, что f(z
)=g(z
).
Соединим точки z0
и z
произвольной непрерывной линией LG
.Обозначим d=dist(L,G).
Ясно, что круг с центром в любой точке
линии L
и радиусом
)
Пусть G
– произвольная область, f(z)=g(z)
на бесконечном множестве EG
и Е
имеет предельную точку z0G.
Пусть z
- произвольная точка области G.
Покажем, что f(z
)=g(z
).
Соединим точки z0
и z
произвольной непрерывной линией LG
.Обозначим d=dist(L,G).
Ясно, что круг с центром в любой точке
линии L
и радиусом 
 целиком лежит в G.
По доказанному f(z)=g(z)
всюду внутри круга
целиком лежит в G.
По доказанному f(z)=g(z)
всюду внутри круга
 ,
так как z0
- предельная точка множества Е.
Пусть центр этого круга непрерывно
перемещается по L
от z0
к z.
Тогда f(z)=g(z)
все время внутри круга. Следовательно,
в частности, f(z
)=g(z
).
Так как
z
,
так как z0
- предельная точка множества Е.
Пусть центр этого круга непрерывно
перемещается по L
от z0
к z.
Тогда f(z)=g(z)
все время внутри круга. Следовательно,
в частности, f(z
)=g(z
).
Так как
z - произвольная точка, то f(z)=g(z)
всюду в области G.
- произвольная точка, то f(z)=g(z)
всюду в области G.
Замечание.
Из теоремы следует, что функции
f(z)
и g(z) аналитические в области G,
тождественно равны между собой, если
аналитические в области G,
тождественно равны между собой, если
1) f(z)=g(z) всюду в произвольной малой окрестности точки области G;
2) f(z)=g(z) на произвольной малой линии, целиком лежащей в G.
Это - одно из замечательных свойств аналитических функций. В случае же произвольной непрерывной функции комплексного переменного ее значения в окрестности точки не определяют ее значения во всех точках области.
Нули аналитической функции
Пусть
f(z)
- аналитическая в области G
функция. Нулем
функции называется точка
z0G
 ,
в которой
f(z0)
,
в которой
f(z0) =0.
=0.
Множество
нулей функции f(z),
лежащих в области G,
может быть конечным или бесконечным,
но никакая точка области G
не может быть предельной точкой множества
нулей, если
 .
Отсюда следует, что любое ограниченное
замкнутое множество точек F
области G
может содержать лишь конечное число
нулей функции f(z).
Действительно, если допустим противное:
F
содержит бесконечное множество нулей,
то получим, что множество имеет предельную
точку, принадлежащую множеству
.
Отсюда следует, что любое ограниченное
замкнутое множество точек F
области G
может содержать лишь конечное число
нулей функции f(z).
Действительно, если допустим противное:
F
содержит бесконечное множество нулей,
то получим, что множество имеет предельную
точку, принадлежащую множеству
 ,
а, следовательно, принадлежащую множеству
G.
,
а, следовательно, принадлежащую множеству
G.
Пусть
f(z)
- аналитическая в области G,
 и в точке z0
и в точке z0
 f(z0)
=0.
Тогда разложение для некоторой окрестности
точки z0
имеет вид
f(z0)
=0.
Тогда разложение для некоторой окрестности
точки z0
имеет вид
 ,
,
т.к а0=f(z0)=0.
Очевидно, все коэффициенты разложения не могут быть равны 0, т.к в этом случае было бы f(z)≡0 (по теореме единственности). Следовательно, среди коэффициентов аn (n=1,2...) есть отличные от нуля. Обозначим номер наименьшего из них через m (m≥1). Тогда а1=а2=...=аm-1=0, am≠0, и, следовательно, разложение f(z) имеет вид
f(z)=am∙(z-z0)m+am+1∙(z-z0)m+1+...
В этом случае точка z0 – нуль порядка m для функции f(z). Если m=1, то нуль называется простым, при m>1- кратным. Простой нуль характеризуется тем, что для него f(z0)=0, f(z0)≠0 (т.к. , n=1,2…), кратный нуль порядка m≥2 характеризуется соотношениями f(z0)=0, f(z0)=0,…, f(m-1)(z0)=0, f(m)(z0)≠0.
Все сказанное имеет место и для тех точек области G, для которых f(z0)=А, т.к. эти точки являются нулями, аналитической функции f(z0)-A. Точки, в которых f(z0)=А, называются А- точками аналитической функции f(z).
Вопрос №17. Понятие ряда Лорана. Теорема об сходимости.
Ряд Лорана, область сходимости
Рассмотрим ряд, расположенный по целым отрицательным степеням z-z0:
А0+A1∙(z-z0)-1+A2∙(z-z0)-2+…+An∙(z-z0)-n+…. (1)
Полагая
 ,
получим обычный степенной ряд
,
получим обычный степенной ряд
A0+A1t+A2t2+…+Antn+... . (2)
Радиус
сходимости ряда (2) по теореме Коши-
Дамара
 .
.
1) Если 0<R<∞
, то ряд (2) абсолютно сходится в круге
 <R
и расходится вне его, т.е при
>R.
Вернемся к переменной z:
<R
и расходится вне его, т.е при
>R.
Вернемся к переменной z:
 .
Следовательно, при
.
Следовательно, при
 ряд (1) сходится абсолютно, а при
ряд (1) сходится абсолютно, а при
 ряд (1) расходится.
ряд (1) расходится.
2) Если
R=0,
то ряд (2) сходится только в точке t=0.
Значит, при
 =∞
ряд (1) расходится во всей конечной к
плоскости.
=∞
ряд (1) расходится во всей конечной к
плоскости.
3) Если R=∞, то ряд (2) абсолютно сходится во всей конечной комплексной плоскости. Поэтому, если =0, то ряд (1) абсолютно сходится во всей конечной плоскости, кроме точки z=z0.
Обозначим через r= .
Итак, область сходимости ряда (1) – это внешность круга |z-z0|<r, т.е область |z-z0|>r (при r- конечном). При r=0 она превращается во всю конечную плоскость, кроме точки z=z0. При r=∞ она вырождается в точку z=∞.
Обозначим
 .
Т. к. ряд (2) сходится равномерно внутри
.
Т. к. ряд (2) сходится равномерно внутри
 ,
то ряд (1) равномерно сходится внутри К
и определяет функцию
,
то ряд (1) равномерно сходится внутри К
и определяет функцию
F(z)=А0+A1∙(z-z0)-1+A2∙(z-z0)-2 +…+An∙(z-z0)-n+…, (1׳)
которая является аналитической во всех конечных точках области К. При z=∞ F(∞)=A0. Будем по определению F(z) называть аналитической в бесконечно удаленной точке. Т.о., аналитичность в точке z=∞ характеризуется наличием разложения (1′), сходящимся в некоторой окрестности точки z=∞.
Определение. Рядом Лорана называется функциональный ряд
 , (3)
, (3)
который является суммой рядов
(4) и  . (5)
. (5)
Определение. Ряд Лорана называется сходящимся на множестве D, если на этом множестве сходится каждый из рядов (4) и (5). Суммой ряда Лорана называется функция S(z)=S1(z)+S2(z), где S1(z) и S2(z)- суммы рядов (4) и (5).
Ряд Лорана называется абсолютно сходящимся на D, если на этом множестве абсолютно сходятся ряды (4) и (5).
Ряд Лорана называется равномерно сходящимся на D, если на этом множестве равномерно сходятся ряды (4) и (5).
Ряд (4) называется правильной частью ряда Лорана, ряд (5)- его главной частью.
Теорема 1.
1) Область сходимости ряда Лорана есть круговое кольцо. Ряд Лорана абсолютно сходится в этом кольце и равномерно сходится в каждой замкнутой его части.
2) Сумма ряда Лорана является аналитической функцией.
Д оказательство.
оказательство.
1)Обозначим
 =Λ,
=Λ,
 =r.
Тогда ряд (4) сходится абсолютно и
равномерно внутри области
=r.
Тогда ряд (4) сходится абсолютно и
равномерно внутри области
 ,
т.е. внутри окружности
,
т.е. внутри окружности
 ,
и расходится вне этой окружности. Ряд
(5) сходится
абсолютно и равномерно внутри области
g:
|z-z0|>r,
т.е вне окружности γ:|z-z0|=r
и расходится внутри γ.
Области G
и g
имеют общие точки тогда и только тогда,
когда выполнено r<R.
В этом случае G∩g=D={z:
r<|z-z0|<R}
- круговое кольцо. Внутри области D
оба ряда сходятся в каждой его замкнутой
части абсолютно и равномерно, следовательно,
внутри D
абсолютно и равномерно сходится ряд
Лорана (3). В каждой точке вне D
один из рядов (4) или (5) расходится,
следовательно, вне D
ряд (3) расходится.
,
и расходится вне этой окружности. Ряд
(5) сходится
абсолютно и равномерно внутри области
g:
|z-z0|>r,
т.е вне окружности γ:|z-z0|=r
и расходится внутри γ.
Области G
и g
имеют общие точки тогда и только тогда,
когда выполнено r<R.
В этом случае G∩g=D={z:
r<|z-z0|<R}
- круговое кольцо. Внутри области D
оба ряда сходятся в каждой его замкнутой
части абсолютно и равномерно, следовательно,
внутри D
абсолютно и равномерно сходится ряд
Лорана (3). В каждой точке вне D
один из рядов (4) или (5) расходится,
следовательно, вне D
ряд (3) расходится.
2)
 - аналитическая функция (как сумма
степенного ряда) в |z-z0|<R.
- аналитическая функция (как сумма
степенного ряда) в |z-z0|<R.
-
аналитическая функция zz0.
Сумма ряда
 -
аналитическая в
-
аналитическая в
 .
Следовательно,
.
Следовательно,
 также аналитическая функция в |z-z0|>r
(т.к. композиция аналитических функций
– аналитическая функция, по теореме о
производной сложной функции). Следовательно,
f(z)=S1(z)+S2(z)=
- аналитическая функция в кольце D.
также аналитическая функция в |z-z0|>r
(т.к. композиция аналитических функций
– аналитическая функция, по теореме о
производной сложной функции). Следовательно,
f(z)=S1(z)+S2(z)=
- аналитическая функция в кольце D.
В дальнейшем будем считать, что r<R.
Теорема 2. Если функция f(z) разлагается в кольце D={z: r<|z-z0|<R} в ряд Лорана, то это разложение единственно.
Доказательство.
Пусть  (6).
(6).
Пусть ρ: r<ρ<R. Тогда ряд (6) будет равномерно сходиться на окружности γ: |z-z0|=ρ (по теореме 1). Тогда ряд
 (7)
(7)
 будет
равномерно сходиться, т.к функция
будет
равномерно сходиться, т.к функция
 ограничена по модулю
ограничена по модулю
 .
Следовательно, этот ряд (7) можно почленно
интегрировать на окружности .
Тогда
.
Следовательно, этот ряд (7) можно почленно
интегрировать на окружности .
Тогда
 . (8)
. (8)
Рассмотрим интеграл в правой части.
1)
n≠k: 

 .
.
2)
n=k.
В этом случае
 (доказывали раньше).
(доказывали раньше).
Следовательно, в сумме правой части (8) все слагаемые равны нулю, кроме слагаемого с номером к. Тогда из (8) получим
 . (9)
. (9)
Формула (9) выражает
коэффициенты ряда Лорана через его
сумму f(z)
(аналогична формуле для коэффициентов
степенного ряда, но там
 ,
а здесь
!)
,
а здесь
!)
Докажем единственность разложения. Пусть
,
 .
.
Эти ряды сходятся в кольцах D и ∆ соответственно, содержащих окружность γ:|z-z0|=ρ и f(z)=φ(z) на γ. Тогда из (9) следует, что ak=bk ( ). Следовательно, ряды тождественны. В частности, если D=∆, то f(z)=φ(z) z∈D.
Как найти кольцо
сходимости ряда Лорана? Для этого надо
знать r
и R.
Правильная часть сходится в круге
|z-z0|<R,
где
 или
или
 .
Главная часть сходится при |z-z0|>r,
где
.
Главная часть сходится при |z-z0|>r,
где
 или
или
 (получается с помощью замены
).
(получается с помощью замены
).
Разложение аналитической функции в ряд Лорана
Теорема 3
(Лорана). Каждая функция f(z),
однозначная и аналитическая в круговом
кольце D={r<|z-z0|<R},
представляется в этом кольце сходящимся
рядом Лорана:
 .
.
Вопрос №18. Теорема о поведении функции в окрестности изолир. точки.
Теорема1. Изолированная особая точка является устранимой особой точкой функции f(z) тогда и только тогда, когда f(z) является ограниченной в некоторой проколотой окрестности точки z0.
Доказательство.
1) Необходимость. Пусть z0- устранимая особая точка f(z), тогда по определению
 . (2)
. (2)
Степенной
ряд в правой части сходится в
 .
Сумма S(z)
степенного ряда является аналитической
в
.
Следовательно, она непрерывна в
,
причем
.
Сумма S(z)
степенного ряда является аналитической
в
.
Следовательно, она непрерывна в
,
причем
 ,
т.е.
,
т.е.
 .
Следовательно, переходя к
.
Следовательно, переходя к
 в (2), получим
в (2), получим
 .
Т.к. существует конечный предел в точке
z0
функции
f(z),
то f(z)
ограничена в некоторой окрестности z0.
.
Т.к. существует конечный предел в точке
z0
функции
f(z),
то f(z)
ограничена в некоторой окрестности z0.
2 )
Достаточность. Пусть f(z)
аналитическая и ограниченная в
,
т.е.
)
Достаточность. Пусть f(z)
аналитическая и ограниченная в
,
т.е.
 .
Разложим функцию в ряд Лорана:
.
Разложим функцию в ряд Лорана:
 .
Докажем, что все коэффициенты с
отрицательными степенями равны нулю.
.
Докажем, что все коэффициенты с
отрицательными степенями равны нулю.
 ,
где
,
где
 .
.
 .
.
Пусть
n<0.
Перейдем в последнем неравенстве к
 при фиксированном n:
при фиксированном n:
 .
Следовательно, z0
- устранимая особая точка f(z).
.
Следовательно, z0
- устранимая особая точка f(z).
Замечание. Если z0-устранимая особая точка f(z), то функцию f(z) можно доопределить так, чтобы она стала аналитической в z0:
 где
где
 ,
тогда
,
тогда
 будет аналитической в z0,
т.к. она совпадает с суммой ряда Тейлора.
будет аналитической в z0,
т.к. она совпадает с суммой ряда Тейлора.
Теорема
2.
Изолированная особая точка
z0
является устранимой особой точкой
функции f(z)
тогда и только тогда, когда
 .
.
Доказано в теореме 1.
Теорема
3.
Изолированная особая точка
z0
является полюсом m-го
порядка функции f(z)
тогда и только тогда, когда существует
функция F(z),
аналитическая в некоторой окрестности
,
такая, что
 .
.
Доказательство.
