
1) Необходимость.
Пусть
z0
- полюс m-
го порядка функции f(z).
Тогда по определению разложение f(z)
в
 имеет вид
имеет вид
 ,
,
где
 .
Умножим обе части на
.
Умножим обе части на
 :
:
 .
.
Обозначим
 -
аналитическая в
-
аналитическая в
 как сумма степенного ряда,
как сумма степенного ряда,
 ,
тогда
,
тогда
 .
Отсюда
.
Отсюда
 ,
где
,
где
 ,
F(z)
-
аналитическая функция.
,
F(z)
-
аналитическая функция.
2) Достаточность.
Пусть
существует функция
F(z),
аналитическая в
и

 ,
такая, что
,
такая, что
 .
Так как F(z)
- аналитическая, то она разлагается в
ряд Тейлора с центром в точке
z0:
.
Так как F(z)
- аналитическая, то она разлагается в
ряд Тейлора с центром в точке
z0:

 ,
причём
,
причём
 .
Тогда
.
Тогда
 .
.
Главная
часть содержит
 слагаемых, следовательно, z0-
полюс
-го
порядка функции f(z).
слагаемых, следовательно, z0-
полюс
-го
порядка функции f(z).
Теорема
4.
Изолированная особая точка z0
является полюсом функции f(z)
тогда и только тогда, когда
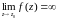 .
.
Доказательство.
1) Необходимость.
Пусть
z0
полюс функции f(z),
тогда
по
теореме 3 существует функция F(z),
аналитическая в
,
такая, что
и
.
Перейдем к
 :
:
 ,
так как
,
так как
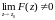 ,
а
,
а
 =0.
=0.
2) Достаточность.
Пусть
z0
- изолированная особая точка и
.
Тогда
 .
Следовательно,
.
Следовательно,
 ограничена в окрестности точки z0,
значит,
по теореме 1 z0-устранимая
особая точка для функции
ограничена в окрестности точки z0,
значит,
по теореме 1 z0-устранимая
особая точка для функции
 и
и
 ,
где
,
где
 -коэффициент
в разложении Лорана для функции
(главная часть=0), то есть
-коэффициент
в разложении Лорана для функции
(главная часть=0), то есть
 .
.
Пусть
 - первый ненулевой коэффициент в ряде
справа (то есть
- первый ненулевой коэффициент в ряде
справа (то есть
 ).
Тогда
).
Тогда
 .
.
Обозначим
 - аналитическая в
- аналитическая в
 как сумма степенного ряда и
как сумма степенного ряда и
 ,
следовательно,
,
следовательно,
 .
Отсюда
.
Отсюда
 .
Обозначим
.
Обозначим
 -
аналитическая в
и
-
аналитическая в
и
 .
Тогда
,
и
по теореме 3 z0
- полюс
-го
порядка функции
.
Тогда
,
и
по теореме 3 z0
- полюс
-го
порядка функции
 .
.
Из теоремы 3 следует также
Теорема
5.
Точка
z0
является полюсом
-
го порядка функции f(z)
тогда и только тогда, когда она является
нулём
-го
порядка для функции
 при zz0.
при zz0.
Доказательство.
1)
Необходимость. Пусть z0
- полюс m-го
порядка функции f(z).
Тогда по теореме 3
 ,
где
,
где .
Тогда
.
Тогда
 .
.
Так
как
,
то

 – аналитическая в точке z0
и
– аналитическая в точке z0
и
 .
Следовательно, z0-
нуль
-го
порядка функции
.
.
Следовательно, z0-
нуль
-го
порядка функции
.
2) Достаточность.
Пусть
z0
- нуль
–
го порядка функции
.
Тогда
 ,
где
,
где - аналитическая в точке z0
и
- аналитическая в точке z0
и

 .
Отсюда
.
Отсюда
 ,
где
,
где
 - аналитическая в точке z0
и
- аналитическая в точке z0
и
 .
Тогда
.
Тогда  по
теореме 3 z0
- полюс
-го
порядка функции f(z).
по
теореме 3 z0
- полюс
-го
порядка функции f(z).
-
Теорема 6
(А.В.Сохоцкого).
Каково бы ни было комплексное число
 (конечное или бесконечное), найдётся
такая последовательность точек {zn},
сходящаяся к существенно особой точке
z0
,
что
(конечное или бесконечное), найдётся
такая последовательность точек {zn},
сходящаяся к существенно особой точке
z0
,
что
 .
.
(Короче можно сформировать следующим образом: в сколь угодно малой окрестности существенно особой точки f(z) принимает значения сколь угодно близкие к любому наперед заданному числу, конечному или бесконечному.)
Доказательство.
1)
А=.
Тогда утверждение справедливо, т.к.
функция не ограничена в окрестности
существенно особой точки (следовательно,
 ).
).
2) A .
От противного. Пусть в произвольной
окрестности нет точек, в которых значения
функции сколь угодно близки к А.
Значит,
.
От противного. Пусть в произвольной
окрестности нет точек, в которых значения
функции сколь угодно близки к А.
Значит,
 и
и
 :
:

 .
Положим
.
Положим
 - аналитическая в
- аналитическая в
 и
и
 ,
т.е.
,
т.е.
 ограничена
по модулю. Значит, по теореме 1 z0
- устранимая особая точка функции
.
Следовательно,
ограничена
по модулю. Значит, по теореме 1 z0
- устранимая особая точка функции
.
Следовательно,
 .
Но так как f(z)
не ограничена по модулю ни в какой
окрестности точки
z0,
то
.
Но так как f(z)
не ограничена по модулю ни в какой
окрестности точки
z0,
то
 ,
то есть функция
,
то есть функция
 имеет нуль в точке z0.
А значит, функция f(z)-A
(по теореме 5) имеет полюс в точке z0.
Полученное противоречие доказывает
теорему.
имеет нуль в точке z0.
А значит, функция f(z)-A
(по теореме 5) имеет полюс в точке z0.
Полученное противоречие доказывает
теорему.
