
- •Вопрос 1. Комплексные числа и действия над ними. Алгебраич. Форма записи числа. Геометрич. Интерпретация компл. Числа. Модуль и аргумент.
- •Вопрос 2. Модуль и аргумент комплексного числа. Тригоном. И показательная форма записи комплексного числа. Действия с компл. Числами, записан…
- •Вопрос 3. Определение предела послед. Комплексных чисел и его геом.Смысл. Необх. И достат. Условие. Критерий Коши. Бесконечно удаленная точка.
- •Вопрос 4. Комплексно-значные функции действ. Переменной. Кривые на комплекс. Пл. Функции комплекс. Переменного. Геометрич. Интерпритация.
- •Геометрическая интерпретация функции комплексного переменного.
- •Вопрос 5. Определение предела функции. Необходим. И достаточное условие. Непрерывность функций. Примеры.
- •Вопрос 6. Понятие производной функции комплекс. Переменной. Определение функции диф. В точке и области. Теорема о непрерывности. Правила диф.
- •Вопрос 7. Определение функции диф. В точке и области. Необходимые и достаточные условия дифференцируемости функции.
- •Вопрос 8. Геометрический смысл аргумента и модуля производной. Понятие конфорного отображения.
- •Вопрос 9. Общие степенная и показательная функции. Логарифм.
- •Вопрос 10. Понятие интеграла от функции комплекс. Переменного и свойства.
- •Вопрос 11. Понятие числового ряда в комплексной области. Сходимость. Критерий Коши.
- •Вопрос 12. Последовательности и ряды функций комплексного переменного
- •Вопрос 13. Изолированные особые точки и их классификация.
- •Вопрос 14. Бесконечно удаленная изолированная особая точка
Вопрос 2. Модуль и аргумент комплексного числа. Тригоном. И показательная форма записи комплексного числа. Действия с компл. Числами, записан…
Длина r вектора ОМ называется модулем комплексного числа z и обозначается |z|.
r=|z|= .
Угол φ - угол между положительным направлением оси ОХ и вектором ОМ называется аргументом комплексного числа z и обозначается: Arg z (-∞<φ< ∞).
Для числа z=0 аргумент не определён.
Для любого комплексного числа (кроме z=0) Arg z может быть найден из системы
которая имеет, вообще говоря, бесконечное множество решений. Все они содержатся в формуле φ=φ0+2πk, k , где φ0–одно из решений системы.
начение φ0, удовлетворяющее условию -π <φ0<π , называется главным значением аргумента и обозначается: arg z. Таким образом,
Arg z=argz+2πk, k .
Очевидно, что tg(arg z)=
Так как x=rcosφ, y=rsinφ, то z=x+i·y=rcosφ+i·rsinφ, z=r(cosφ+i·sinφ) -
тригонометрическая форма записи комплексного числа.
Рассмотрим действия с комплексными числами, записанными в тригонометрической форме
Пусть z1=r(cosφ+i·sinφ), z2=ρ(cosψ+i·sinψ).
z1·z2=rρ(cosφ+i·sinφ)·(cosψ+i·sinψ)=
=rρ(cosφcosψ-sinφsinψ+i(sinφcosψ+cosφsinψ))=rρ(cos(φ+ψ)+sin(φ+ψ)).
То есть
|z1·z2 =|z1|·|z2|, Arg(z1·z2)=Argz1+Argz2.
Модуль произведения двух комплексных чисел равен произведению их модулей, аргумент произведения двух комплексных чисел равен сумме аргументов сомножителей.
Это правило распространяется на случай любого конечного числа сомножителей.
В частности, если все сомножители равны, получим
|zⁿ|=|z|ⁿ, Arg(zⁿ)=nArg(z), или
zⁿ=(r(cosφ+isinφ))ⁿ=rⁿ(cos(nφ)+isin(nφ)) – формула Муавра.
Пусть z ≠0. Корнем натуральной степени из комплексного числа z называется такое комплексное число w, которое будучи возведено в n-ю степень даёт число z, то есть wn=z.
Очевидно, |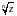 |=
|= ,
, 
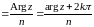 .
.
Или если z= r(cosφ+i·sinφ), то
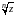 =
=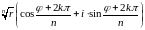 ,
k
=
0, 1, 2, …, n-1,
-π<φ≤π.
,
k
=
0, 1, 2, …, n-1,
-π<φ≤π.
То есть
среди значений
различными являются только n.
Геометрически они изображаются вершинами
правильного n-угольника,
вписанного в окружность с центром в
точке О(0;0),
радиуса
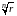 .
.
Определение.
Частным
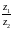 комплексного
числа
z1
и z2
≠0
называется
комплексное число z,
такое что z·z2=z1.
комплексного
числа
z1
и z2
≠0
называется
комплексное число z,
такое что z·z2=z1.
Из определения частного и правила умножений комплексных чисел
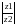 =
=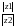 , Arg
, Arg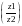 =Argz1-Argz2.
=Argz1-Argz2.
Итак, если z1=r(cosφ+i·sinφ), z2=ρ(cosψ+i·sinψ).
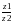 =
=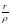 (cos(φ-ψ)+i·sin(φ-ψ))
(cos(φ-ψ)+i·sin(φ-ψ))
.
Модуль частного двух комплексных чисел равен частному их модулей, аргумент частного двух комплексных чисел равен разности аргументов делимого и делителя.
Используя формулу Эйлера eiφ=cosφ+i·sinφ
Из тригонометрической формы записи комплексного числа получаем показательная форму записи z=reiφ.
В показательной форме операции над комплексными числами принимают более наглядный вид. Пусть z1= reiφ, z2=ρeiψ. Тогда
z 1z2=rρei(φ+ψ), zⁿ=rⁿ einφ,
=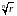
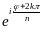 ,-π<φ≤π,
k=1,
2, …, n-1,
,-π<φ≤π,
k=1,
2, …, n-1,
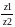 =
=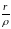
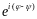 ,
z20.
,
z20.
Вопрос 3. Определение предела послед. Комплексных чисел и его геом.Смысл. Необх. И достат. Условие. Критерий Коши. Бесконечно удаленная точка.
Пусть {zn}: z1, z2, …, zn, … - последовательность комплексных чисел.
Определение.
Комплексное число z0
называется пределом
числовой последовательности {zn},
если ρ(zn
,z0)=|zn-z0| 0.
0.
Это можно записать следующим образом:
 ε>0
N
ε>0
N :
n>N
|zn-z0|<ε.
:
n>N
|zn-z0|<ε.
Геометрический смысл. Точка z0 является предельной точкой последовательности {zn}, если какой бы малый круг радиуса ε с центром в точке z0 ни взять, всегда можно указать номер N, начиная с которого все члены последовательности лежат в этом круге.
Определение. Если последовательность {zn} имеет конечный предел, то она называется сходящейся.
Теорема
1.
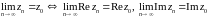 .
.
Доказательство.
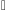 1) Пусть
1) Пусть
 .
Тогда ε>0
N
:n>N
выполнено
|zn-z0|<ε.
.
Тогда ε>0
N
:n>N
выполнено
|zn-z0|<ε.
Так как
|Re(zn-z0)|≤|zn-z0|<ε,
то
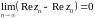 ,
отсюда
,
отсюда
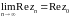 .
.
Так как
|Im(zn-z0)|≤|zn-z0|<ε,
то
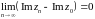 ,
отсюда
,
отсюда
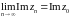 .
.
2) Пусть и .
По
определению ε>0
N1 :
n>N1
|Rezn–Rez0|=|Re(zn-z0)|<
:
n>N1
|Rezn–Rez0|=|Re(zn-z0)|<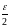 ,
,
ε>0 N2 : n>N2 |Imzn–Imz0|=|Im(zn-z0)|< .
Пусть N=max{N1,N2}. Тогда n>N для выбранного ε>0
|zn-z0|<|Re(zn-z0)|+|Im(zn-z0)|<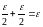 ,
следовательно
.
,
следовательно
.
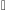
Теорема 3 (критерий Коши сходимости последовательности комплексных чисел).
Для
того, чтобы последовательность комплексных
чисел {zn}
сходилась, необходимо и достаточно,
чтобы ε>0
N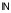 :
n>N,
m
выполнялось |zn+m–zn|<ε.
:
n>N,
m
выполнялось |zn+m–zn|<ε.
Доказательство.
1) Пусть
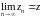 .
Тогда ε>0
N
:
n>N
выполняется |zn–z|<
.
Тогда ε>0
N
:
n>N
выполняется |zn–z|<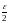 .
.
Тогда |zn+m–zn|=|zn+m–z+z-zn|≤|zn+m–z|+|zn–z|< + =ε m .
2) Пусть
ε>0
N
:
n>N,
m
выполняется |zn+m–zn|<ε.
Тогда |Re(zn+m–zn)|=|Rezn+m
–Rezn|<ε
и |Im(zn+m–zn)|=|Imzn+m–Imzn|<ε.
Следовательно, последовательности
действительных чисел {Rezn
и {Imzn
фундаментальные. Согласно критерию
Коши сходимости последовательности
действительных чисел они сходятся
(последовательность фундаментальна
тогда и только тогда, когда она сходится).
То есть
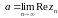 и
и 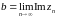 Тогда по теореме 1
Тогда по теореме 1
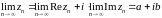 .
Следовательно, {zn
}
сходится.
.
Следовательно, {zn
}
сходится.
Дополним
множество
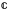 элементом ∞, который называют
бесконечностью. Элементу ∞ поставим в
соответствие бесконечно удаленную
точку на комплексной плоскости.
элементом ∞, который называют
бесконечностью. Элементу ∞ поставим в
соответствие бесконечно удаленную
точку на комплексной плоскости.
Определение. ε – окрестностью точки ∞ называется внешность круга с центром в точке О(0;0) и радиуса ε: |z|>ε.
Определение.
 ε>0
N
:
n>N
выполняется |zn|>ε.
ε>0
N
:
n>N
выполняется |zn|>ε.
Геометрически это означает, что ε, сколь угодно большого, все члены последовательности {zn }, начиная с некоторого номера N, лежат вне круга с центром в точке (0;0), радиуса ε, то есть в окрестности точки ∞.
Из
определения следует, что условие
 эквивалентно условию
эквивалентно условию
 .
Присоединяя к множеству
элемент ∞, получим расширенное
множество комплексных чисел
.
Присоединяя к множеству
элемент ∞, получим расширенное
множество комплексных чисел
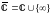 .
.
Комплексная плоскость, дополненная бесконечно удаленной точкой, называется расширенной комплексной плоскостью. Бесконечно удаленная точка, как и нулевая, не имеет аргумента. Не определены также понятия действительной и мнимой части точки ∞. Многие свойства бесконечно больших последовательностей действительных чисел сохраняются и в :
1)
a±∞=∞, 3)
a∞=∞
(а0), 5)
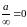 ,
,
2)
∞+∞=∞, 4)
∞∞=∞, 6)
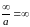 (а0).
(а0).
Ч тобы
получить наглядное изображение
расширенной комплексной плоскости,
рассмотрим сферу S,
касающуюся комплексной плоскости в
точке О.
Обозначим через Р
точку сферы, диаметрально противоположную
точке О.
Каждой точке z
комплексной плоскости поставим в
соответствие точку М
сферы, которая является пересечением
сферы S
и прямой, соединяющей точки Р
и z.
Таким образом, мы получаем взаимно-однозначное
соответствие между точками комплексной
плоскости и точками сферы с выколотой
точкой Р
(т. к. точке Р
не соответствует ни какая конечная
точка плоскости
).
тобы
получить наглядное изображение
расширенной комплексной плоскости,
рассмотрим сферу S,
касающуюся комплексной плоскости в
точке О.
Обозначим через Р
точку сферы, диаметрально противоположную
точке О.
Каждой точке z
комплексной плоскости поставим в
соответствие точку М
сферы, которая является пересечением
сферы S
и прямой, соединяющей точки Р
и z.
Таким образом, мы получаем взаимно-однозначное
соответствие между точками комплексной
плоскости и точками сферы с выколотой
точкой Р
(т. к. точке Р
не соответствует ни какая конечная
точка плоскости
).
Рассмотрим последовательность {zn} комплексных чисел: zn ∞. Каждой точке zn этой последовательности соответствует точка Мn сферы. Очевидно Мn Р. Поэтому точку Р принимают за изображение бесконечно удаленной точки (т.е. точке ∞ соответствует точка Р сферы).
Построенное взаимно-однозначное соответствие между точками расширенной комплексной плоскости и точками сферы S называется стереографической проекцией, а сфера S – сферой Римана. Таким образом, комплексные числа расширенной комплексной плоскости можно изобразить точками сферы. Преимущество в том, что наглядно изображается точка ∞.
