
- •Вопрос 1. Комплексные числа и действия над ними. Алгебраич. Форма записи числа. Геометрич. Интерпретация компл. Числа. Модуль и аргумент.
- •Вопрос 2. Модуль и аргумент комплексного числа. Тригоном. И показательная форма записи комплексного числа. Действия с компл. Числами, записан…
- •Вопрос 3. Определение предела послед. Комплексных чисел и его геом.Смысл. Необх. И достат. Условие. Критерий Коши. Бесконечно удаленная точка.
- •Вопрос 4. Комплексно-значные функции действ. Переменной. Кривые на комплекс. Пл. Функции комплекс. Переменного. Геометрич. Интерпритация.
- •Геометрическая интерпретация функции комплексного переменного.
- •Вопрос 5. Определение предела функции. Необходим. И достаточное условие. Непрерывность функций. Примеры.
- •Вопрос 6. Понятие производной функции комплекс. Переменной. Определение функции диф. В точке и области. Теорема о непрерывности. Правила диф.
- •Вопрос 7. Определение функции диф. В точке и области. Необходимые и достаточные условия дифференцируемости функции.
- •Вопрос 8. Геометрический смысл аргумента и модуля производной. Понятие конфорного отображения.
- •Вопрос 9. Общие степенная и показательная функции. Логарифм.
- •Вопрос 10. Понятие интеграла от функции комплекс. Переменного и свойства.
- •Вопрос 11. Понятие числового ряда в комплексной области. Сходимость. Критерий Коши.
- •Вопрос 12. Последовательности и ряды функций комплексного переменного
- •Вопрос 13. Изолированные особые точки и их классификация.
- •Вопрос 14. Бесконечно удаленная изолированная особая точка
Вопрос 13. Изолированные особые точки и их классификация.
Определение. Точка z0 называется правильной (регулярной) точкой функции f(z), если f(z) является аналитической в точке z0 (т.е. является аналитической в некоторой окрестности точки z0).
Определение. Точка z0 называется особой точкой функции f(z), если f(z) не является аналитической в точке z0 (т.е. не является аналитической ни в какой окрестности точки z0 )
Пусть f(z) однозначная функция.
Определение.
Точка
z0
называется изолированной
особой точкой
функции
f(z),
если f(z)
является аналитической в некоторой
проколотой окрестности точки
z0
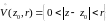 ,
но не определена или не дифференцируема
в самой точке z0
(т.е. z0
– изолированная особая точка, если
z0
- особая точка и f(z)
- аналитическая в
,
но не определена или не дифференцируема
в самой точке z0
(т.е. z0
– изолированная особая точка, если
z0
- особая точка и f(z)
- аналитическая в
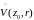 ).
).
Классификация изолированных особых точек
Пусть
z0-
изолированная особая точка функции
f(z).Тогда
f(z)
аналитическая в кольце
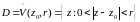 .
Значит, в D
функция разлагается в ряд Лорана с
центром в точке z0.
.
Значит, в D
функция разлагается в ряд Лорана с
центром в точке z0.
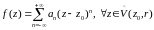 (1)
(1)
Возможны 3 случая.
1) Разложение Лорана (1) не содержит отрицательных степеней. z-z0 (т.е. главная часть равна нулю). В этом случае z0 называется устранимой особой точкой.
2) Разложение Лорана содержит конечное число конечное число отрицательных степеней z-z0 (т.е. главная часть состоит из конечного числа слагаемых). В этом случае z0 называется полюсом.
3) Разложение Лорана содержит бесконечное число отрицательных степеней z-z0 (т.е. главная часть содержит бесконечно много слагаемых). Тогда z0-существенно особая точка функции f(z).
Из определения следует, что
1) В
окрестности устранимой особой точки
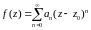 .
.
2) В
окрестности полюса
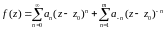 .
.
Число m называется порядком полюса. Если m=1, то полюс называется простым.
В окрестности существенно особой точки
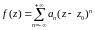 .
.
Вопрос 14. Бесконечно удаленная изолированная особая точка
Бесконечно удаленная изолированная особая точка
До сих пор мы рассматривали только конечные изолированные особые точки. Бесконечно удаленная точка всегда является особой точкой функции f(z).
Определение
1. Точка
z=
называется бесконечно
удаленной
изолированной
особой точкой
функции
f(z),
если
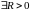 ,
такое что
f(z)
является аналитической в кольце
,
такое что
f(z)
является аналитической в кольце
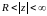 (то
есть в окрестности точки z=).
(то
есть в окрестности точки z=).
Примеры.
1) f(z)=z2. z= - изолированная особая точка, так как других особых точек нет.
2)
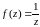 .
Особые точки z=0
и z=.
Они изолированные особые точки.
.
Особые точки z=0
и z=.
Они изолированные особые точки.
3)
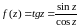 не является аналитической в точках
не является аналитической в точках
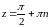 ,
,
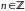 .
Тогда z=
- особая, но не изолированная точка
функции f(z).
.
Тогда z=
- особая, но не изолированная точка
функции f(z).
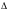
Положим
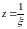 ,
,
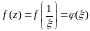 .
Если f(z)
аналитическая при
.
Если f(z)
аналитическая при
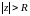 ,
то
,
то
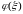 аналитическая в
аналитическая в
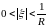 .
Поведение функции
f(z)
в окрестности точки z=
носит тот же характер, что и поведение
в окрестности точки
.
Поведение функции
f(z)
в окрестности точки z=
носит тот же характер, что и поведение
в окрестности точки
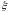
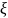 =0.
=0.
Разложим
в ряд Лорана в окрестности точки
=0:
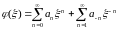 .
Тогда
.
Тогда 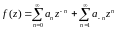 . (*).
. (*).
Поведение
функции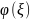 в
окрестности точки
=0
зависит от главной части ряда Лорана
в
окрестности точки
=0
зависит от главной части ряда Лорана
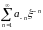 .
.
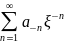 Но
=
Но
= .
Следовательно,
роль главной части ряда Лорана в
окрестности точки z=
играет та часть, которая содержит степени
с положительными степенями
.
.
Следовательно,
роль главной части ряда Лорана в
окрестности точки z=
играет та часть, которая содержит степени
с положительными степенями
.
Тогда возможны 3 случая.
z= является для f(z):
1) устранимой особой точкой, если в разложении (*) нет членов с положительными степенями z;
2) полюсом, если в разложении конечное число членов с положительными степенями;
3) существенно особой точкой, если в разложении (*) бесконечно много членов с положительными степенями.
Свойства изолированных особых конечных точек переносятся на случай z=.
1)
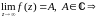 z=
- устранимая особая точка;
z=
- устранимая особая точка;
2)
 z=
- полюс;
z=
- полюс;
3)
 не существует
z=
- существенно особая точка.
не существует
z=
- существенно особая точка.
Примеры.
1)
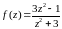 ,
,
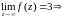 z=
- устранимая особая точка.
z=
- устранимая особая точка.
2)
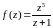 ,
z=
- полюс.
,
z=
- полюс.
3)
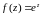 .
не существует (см. пример из п. 4)
z=
- существенно особая точка.
.
не существует (см. пример из п. 4)
z=
- существенно особая точка.
