
- •1.4. Частные производные.
- •3. Выражение является полным дифференциалом.
- •4. Во всех точках области выполняется равенство
- •1) Каждому кратному действительному корню характеристического уравнения соответствует частных решений уравнения вида
- •2) Каждой паре кратных комплексно сопряженных корней и характеристического уравнения соответствует частных решений уравнения вида
- •16Ряды Тейлора и Маклорена.
Лекция1.Функции нескольких переменных
Области и окрестности.
Определение.
Открытой областью (просто областью)
называется множество
 точек
плоскости, удовлетворяющее
условиям:
точек
плоскости, удовлетворяющее
условиям:
Определение. Замкнутой областью называется объединение открытой области и ее границы.
Определение. Область называется ограниченной, если все ее точки принадлежат некоторому кругу с центром в начале координат.
Определение. Область называется односвязной, если все точки, лежащие внутри любой простой замкнутой кривой, полностью расположенной внутри области, также принадлежат области.
Определение.
 окрестностью
точки
окрестностью
точки
 называется
множество точек плоскости
называется
множество точек плоскости
 ,
удовлетворяющих неравенству:
,
удовлетворяющих неравенству:
 .
.
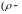 окрестность
точки
окрестность
точки

Определение.
Пусть имеются
два множества:
 и
и
 Переменная
Переменная
 называется
функцией
двух переменных
называется
функцией
двух переменных
 и
и ,
если каждой паре чисел
,
если каждой паре чисел
 из
множества
ставится
в соответствие одно значение переменной
из
множества
ставится
в соответствие одно значение переменной
 .
.
Графическое изображение (график) функции двух переменных.
Рассмотрим
в пространстве прямоугольную систему
координат. Область определения функции
двух переменных изображается некоторым
множеством точек плоскости
.
Каждой точке
 этого
множества можно поставить в соответствие
точку
этого
множества можно поставить в соответствие
точку
 пространства, где
пространства, где
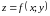 .
Совокупность таких точек принимают за
графическое изображение (график) функции
.
Обычно графиком функции, заданной на
некоторой части плоскости
,
служит некоторая поверхность.
.
Совокупность таких точек принимают за
графическое изображение (график) функции
.
Обычно графиком функции, заданной на
некоторой части плоскости
,
служит некоторая поверхность.
Определение.
Графиком функции
называется
множество точек пространства:
 .
.
Определение.
Линией уровня функции
называется
линия в плоскости
,
определяемая уравнением

Определение
предела
функции в точке.
Число называется пределом функции
при
называется пределом функции
при
 ,
,

1.3.2.Определение.
Число
называется
пределом функции
при

 ,
,
если для если для
любого
 существуют
существуют
 и
и
 зависящие
от
зависящие
от
 ,
такие, что для всех точек
,
такие, что для всех точек
 координаты которых удовлетворяют
неравенствам:
координаты которых удовлетворяют
неравенствам:
 и
и
 выполняется неравенство
выполняется неравенство .
.
Определения
пределов (4случая).
(4случая).
Определение 1
непрерывности в точке. Функция
называется непрерывной в точке
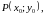 если
она определена в некоторой окрестности
этой точки и
если
она определена в некоторой окрестности
этой точки и
 .
.
Если

 и
и приращения аргументов, а
приращения аргументов, а

Определение 2
непрерывности в точке. Функция
называется непрерывной в точке
если
она определена в некоторой окрестности
этой точки и
 (бесконечно
малым приращениям аргументов соответствует
бесконечно малое приращение функции
).
(бесконечно
малым приращениям аргументов соответствует
бесконечно малое приращение функции
).
Определение. Функция называется непрерывной в области , если она непрерывна в каждой точке этой области.
Определение.
Если функция
непрерывна в окрестности точки ,
а в самой
точке не выполняется условие непрерывности,
то точка
называется точкой разрыва.
,
а в самой
точке не выполняется условие непрерывности,
то точка
называется точкой разрыва.
1.4. Частные производные.
Пусть
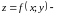 функция
двух переменных
и
.
Будем считать аргумент
постоянным и рассмотрим полученную
функцию одной переменной
.
Допустим, что полученная функция
переменной
дифференцируема.
Ее приращение по этой переменной имеет
вид:
функция
двух переменных
и
.
Будем считать аргумент
постоянным и рассмотрим полученную
функцию одной переменной
.
Допустим, что полученная функция
переменной
дифференцируема.
Ее приращение по этой переменной имеет
вид:
 .
Оно называется частным приращением по
.
.
Оно называется частным приращением по
.
Определение.
Частной производной
по переменной
 от
функции
называется
предел
отношения частного приращения функции
по переменной
к приращению переменной
:
от
функции
называется
предел
отношения частного приращения функции
по переменной
к приращению переменной
:
 .
.
Другие обозначения:

Частная производная по переменной от функции -это ее производная, вычисленная в предположении, что аргумент постоянен.
Определение.
Частной производной
по переменной
 от
функции
называется
предел отношения частного приращения
функции по
к приращению переменной
:
от
функции
называется
предел отношения частного приращения
функции по
к приращению переменной
:
 .
.
Другие обозначения:

Частная производная по переменной от функции -это ее производная, вычисленная в предположении, что аргумент постоянен.
Определение.
Изменение функции
при
совместных изменениях аргументов
независимых
 называют
полным
приращением
функции
двух переменных.
называют
полным
приращением
функции
двух переменных.
Определение. Функция называется дифференцируемой в данной точке , если ее полное приращение можно представить в виде
 ,
где
,
где
 бесконечно
малая более высокого порядка, чем
бесконечно
малая более высокого порядка, чем
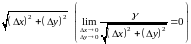 ,
а
и
,
а
и
 не
зависят от
и
не
зависят от
и .
.
Определение.
Главная (линейная относительно приращений
аргументов
и
)
часть приращения функции называется
полным
дифференциалом функции двух переменных:

Теорема. Полный
дифференциал функции
двух переменных
равен сумме произведений частных
производных на дифференциалы
соответствующих
независимых
переменных.
 Определение.
Пусть функция
имеет
частные производные
Определение.
Пусть функция
имеет
частные производные
 и
и
 ,
которые в свою очередь являются функциями
независимых переменных
,
которые в свою очередь являются функциями
независимых переменных и
и

Частные производные от частных производных (если они существуют) называются частными производными второго порядка (вторыми частными производными) от данной функции.
Теорема.
Если вторые смешанные производные
функции
непрерывны, то они равны между собой.
(Без доказательства)

Лекция2. Функции нескольких переменных
Теорема. Если
выражение
 является
полным дифференциалом некоторой функции
является
полным дифференциалом некоторой функции
 (
(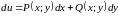 ),
то
),
то
 .
.
Теорема. Если
для двух функций
 и
и
 во
всех точках односвязной области
выполняется
условие
,
то в этой области существует функция
,
полный
дифференциал которой равен
.
во
всех точках односвязной области
выполняется
условие
,
то в этой области существует функция
,
полный
дифференциал которой равен
.
Определение.
Функция
,
полный
дифференциал которой равен
 называется первообразной
от полного дифференциала.
называется первообразной
от полного дифференциала.
Формула,
позволяющая вычислить приближенное
значение функции
в точке
,
если известно ее значение в точке
 имеет
вид:
имеет
вид:

Определение.
Пусть имеются
два множества:
 и
и
 Переменная
Переменная
 называется
функцией
трех переменных
называется
функцией
трех переменных
 и
и ,
если каждой тройке чисел
,
если каждой тройке чисел
 из
множества
ставится
в соответствие одно значение переменной
из
множества
ставится
в соответствие одно значение переменной
 .
.
Обозначение:
 .
.
Определение.
Пусть дана
точка
 Множество
точек трехмерного пространства,
удовлетворяющих неравенству
Множество
точек трехмерного пространства,
удовлетворяющих неравенству
 (внутренняя
часть шара радиуса
(внутренняя
часть шара радиуса
 с
центром в точке
),
с
центром в точке
),
называется
 окрестностью
точки
окрестностью
точки
Определение.
Частные производные функции трех
переменных определяются так:


Определение.
Полное приращение функции трех переменных
определяется так: .
.
Определение.
Полный дифференциал функции трех
переменных определяется так:

Определение. Функция трех переменных называется дифференцируемой в данной точке , если ее полное приращение можно представить в виде
 .
.
Определение.
Пусть имеются
два множества:
 и
Переменная
и
Переменная
 называется
функцией
называется
функцией
 переменных
переменных
 ,
если каждому набору переменных величин
из множества
,
если каждому набору переменных величин
из множества
 соответствует
единственное значение переменной
соответствует
единственное значение переменной

Обозначение:
 .
.
Набор
чисел
 называют
точкой
называют
точкой мерного
пространства. Множество
называется
областью определения функции.
мерного
пространства. Множество
называется
областью определения функции.
Определение.
окрестностью
точки
 называется
множество точек
мерного
пространства, удовлетворяющих неравенству:
называется
множество точек
мерного
пространства, удовлетворяющих неравенству:
 .
.
Такая
окрестность называется открытым
мерным
шаром, а ее граница, определяемая
уравнением
 называется
мерной
сферой.
называется
мерной
сферой.
Определение.
Полным приращением функции
 переменных
называется
переменных
называется
 .
.
Определение.
Частным приращением функции
по переменной
 называется
называется

Определение.
Частной производной функции
по переменной
называется

Определение.
Полным приращением функции
называется

2.3.7. Теорема. Полный дифференциал функции переменных равен сумме произведений частных производных на приращения (дифференциалы) соответствующих независимых переменных. (Без доказательства)
 или
или

Двойным
интегралом
 по области
называется
предел последовательности интегральных
сумм, при условии, что
по области
называется
предел последовательности интегральных
сумм, при условии, что
 ,
если этот предел не зависит от способа
разбиения и выбора точек
,
если этот предел не зависит от способа
разбиения и выбора точек
 :
: .
.
Определение. Цилиндрическим телом называется тело, ограниченное
а)
замкнутой областью
в
плоскости ;
б) поверхностью
;
б) поверхностью
 где
функция
непрерывна
и
неотрицательна в
области
;
в) цилиндрической поверхностью,
у которой
образующая параллельна оси
где
функция
непрерывна
и
неотрицательна в
области
;
в) цилиндрической поверхностью,
у которой
образующая параллельна оси
 ,
а направляющая является границей области
,
а направляющая является границей области

Свойства двойного интеграла
Линейное
свойство.

Если
область интегрирования
разбита
на две
области
 и
и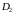 без
общих внутренних точек
без
общих внутренних точек
 ,
то
,
то

Если
во всех точках области интегрирования
функции
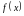 и
и удовлетворяют условию
удовлетворяют условию ,
то
,
то
Оценка
двойного интеграла.
Пусть
 наименьшее
значение
функции,
наименьшее
значение
функции,
 наибольшее
значение
непрерывной функции
в области
,
и пусть
наибольшее
значение
непрерывной функции
в области
,
и пусть
 площадь
области,
тогда:
площадь
области,
тогда: .
.
Теорема
о среднем (в
двойном интеграле).
(Без
доказательства)
Если функция
 непрерывна в области
,
то существует
точка
непрерывна в области
,
то существует
точка
 ,
что
,
что
 ,
где
площадь
области
.
,
где
площадь
области
.
Определение.
Область
называется
правильной
в направлении оси
 ,
если она ограничена
прямыми
,
если она ограничена
прямыми
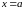 и
и
 и кривыми
и кривыми
 ,
,
 (обе
функции непрерывны на отрезке
(обе
функции непрерывны на отрезке
 ,
и
,
и
 на
нем). (Любая прямая, параллельная оси
пересекает
невертикальную границу области не
более, чем в двух точках.)
на
нем). (Любая прямая, параллельная оси
пересекает
невертикальную границу области не
более, чем в двух точках.)
Определение.
Область
называется
правильной
в направлении оси
 ,
если она ограничена
прямыми
,
если она ограничена
прямыми
 и
и
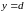 и кривыми
и кривыми
 ,
,
 (обе
функции непрерывны на отрезке
(обе
функции непрерывны на отрезке
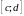 ,
и
,
и
 на
нем.
на
нем.
Двойной интеграл в полярных координатах.
Рассмотрим
в плоскости
полярную систему координат (см.
11.5. 2семестр).
Координатными линиями будут линии
 и
и
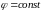 .
Первые представляют собой окружности
с центром в полюсе, а вторые- полупрямые
с началом в полюсе.
.
Первые представляют собой окружности
с центром в полюсе, а вторые- полупрямые
с началом в полюсе.
Частичная область
в полярных координатах представляет
криволинейный четырехугольник,
ограниченный полупрямыми
 и
и
 , а также дугами
и
, а также дугами
и
 .
.
Тогда
 .
.
Так как второе слагаемое бесконечно малая более высокого порядка, чем первое, то
формула
для элемента площади:
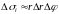 .
.
Поэтому ;
;
 .
.
Интеграл
Эйлера-Пуассона ( ).
).
Ι.Пусть
 квадрат
со стороной
квадрат
со стороной
 ,
и
,
и
 четверти
кругов соответственно радиусов
и
четверти
кругов соответственно радиусов
и
 .
Функция
.
Функция
 положительна,
поэтому двойной интеграл от нее
положителен. Этот интеграл увеличивается
при расширении области интегрирования.
положительна,
поэтому двойной интеграл от нее
положителен. Этот интеграл увеличивается
при расширении области интегрирования.
Поэтому имеет место неравенство:

Вычислим каждый из интегралов, входящих в неравенство (интегралы по областям и с помощью перехода к полярным координатам):
1)
2)

Запишем неравенство, связывающее полученные интегралы:
 .
.
Перейдем
в этом неравенстве к пределу при
 :
:
 Из
последнего равенства следует, что
несобственный интеграл
Из
последнего равенства следует, что
несобственный интеграл сходится,
и имеет место формула: (Интеграл
Эйлера-Пуассона)
сходится,
и имеет место формула: (Интеграл
Эйлера-Пуассона)
 .
.
Лекция 4. Замена переменных в двойном интеграле. Тройной интеграл.
Определение.
Пусть функция
 трех
переменных
задана в
замкнутой ограниченной области
трех
переменных
задана в
замкнутой ограниченной области
 трехмерного
пространства.
Разобьем эту область сетью поверхностей
на конечное число (
трехмерного
пространства.
Разобьем эту область сетью поверхностей
на конечное число ( )
частичных (непересекающихся) областей
пространства с объемами
)
частичных (непересекающихся) областей
пространства с объемами
 где
где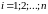 .
В каждой частичной области разбиения
возьмем произвольную точку
.
В каждой частичной области разбиения
возьмем произвольную точку
 и составим интегральную сумму:
и составим интегральную сумму:

Обозначим
через
 наибольший диаметр частичных областей.
Тройным
интегралом от функции
по области
называется
предел последовательности интегральных
сумм, при условии, что
,
если этот предел не зависит от способа
разбиения и выбора точек
:
наибольший диаметр частичных областей.
Тройным
интегралом от функции
по области
называется
предел последовательности интегральных
сумм, при условии, что
,
если этот предел не зависит от способа
разбиения и выбора точек
:
 .
.
Оценка
тройного интеграла.
Пусть
наименьшее
значение
функции,
наибольшее
значение
непрерывной функции
в области
,
и пусть
 объем
этой области, тогда:
объем
этой области, тогда: .
.
Теорема
о среднем (для тройного интеграла).
Если функция
 непрерывна в области
,
то существует точка
непрерывна в области
,
то существует точка
 ,
что
,
что
 .
Вычисление
тройного интеграла в декартовых
координатах.
.
Вычисление
тройного интеграла в декартовых
координатах.
Пусть
область
ограничена
сверху и
снизу
поверхностями:
 и
и
 которые
проектируются
на плоскость
в некоторую ограниченную область
.
Кроме того, область
ограничена цилиндрической поверхностью,
образующие которой параллельны оси
.
Тогда
которые
проектируются
на плоскость
в некоторую ограниченную область
.
Кроме того, область
ограничена цилиндрической поверхностью,
образующие которой параллельны оси
.
Тогда

Если область является криволинейной трапецией правильной в направлении оси (см.3.1.3)
то
Правило замены в тройном интеграле.
Формула перехода
(без доказательства):
 ,
где
,
где
 и
и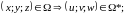
 («якобиан»).
(«якобиан»).
Тройной интеграл в цилиндрических координатах.
Положение
точки
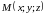 пространства
пространства
 однозначно определяется заданием трех
чисел: а) полярные координаты
однозначно определяется заданием трех
чисел: а) полярные координаты
 (см. 11.5.
2семестр)
точки
(см. 11.5.
2семестр)
точки
 ,
которая является проекцией точки на
плоскость
.
б) аппликата
точки
,
которая является проекцией точки на
плоскость
.
б) аппликата
точки
 .
.
Числа
 называются
цилиндрическими
координатами точки
.
Они связаны с декартовыми координатами
точки
соотношениями:
называются
цилиндрическими
координатами точки
.
Они связаны с декартовыми координатами
точки
соотношениями:
 .
.
Якобиан:
 .
.
Тройной интеграл в сферических координатах.
Положение
точки
пространства
однозначно определяется заданием трех
чисел: а)
длина
радиуса-вектора точки
 ,
,
 угол, который образует проекция этого
радиуса-вектора на плоскость
с
осью
угол, который образует проекция этого
радиуса-вектора на плоскость
с
осью
 ,
,
 угол между радиусом-вектором и осью
угол между радиусом-вектором и осью
 .
.
Числа
 называются
сферическими
координатами точки
называются
сферическими
координатами точки
 Они связаны с декартовыми координатами
точки
соотношениями:
Они связаны с декартовыми координатами
точки
соотношениями:

Якобиан
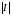 равен
равен .
.
Формула перехода
(см. 4.3.1.):
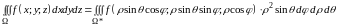
Лекция 5. Криволинейный интеграл первого рода. Криволинейный интеграл второго рода.
Криволинейным
интегралом первого рода (по длине) (по
линии
 )
называется предел последовательности
интегральных сумм
)
называется предел последовательности
интегральных сумм
 при
условии, что наибольшая длина участка
разбиения стремится к нулю.
при
условии, что наибольшая длина участка
разбиения стремится к нулю.

Свойства криволинейных интегралов первого рода.
 где
где
 и
и
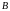 концы
линии
.
концы
линии
.
Вычисление криволинейного интеграла первого рода.
Пусть
линия
задана
параметрическими уравнениями: и
и
 ,
тогда.
,
тогда.
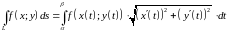
Криволинейным
интегралом
второго
рода (по
координатам) (по линии
 )
называется предел интегральной суммы
)
называется предел интегральной суммы
 при условии, что
наибольшая длина участка разбиения
стремится к нулю.
при условии, что
наибольшая длина участка разбиения
стремится к нулю.

Свойства криволинейных интегралов второго рода.
 .
.
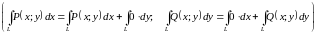

5.2.3.
Вычисление криволинейного интеграла
второго рода.Пусть
линия
задана
параметрическими уравнениями
и
,
тогда ,
где
,
где
 и
и
 значения
параметра, соответствующие началу и
концу линии
значения
параметра, соответствующие началу и
концу линии
Формула
Грина.Если
функции
 и
и
 непрерывны
вместе со своими частными производными
в замкнутой ограниченной области
непрерывны
вместе со своими частными производными
в замкнутой ограниченной области
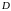 ,
то имеет место
,
то имеет место
формула
Грина
 ,
где
,
где
 граница
области
и
интегрирование по
производится
против часовой стрелки (в положительном
направлении).
граница
области
и
интегрирование по
производится
против часовой стрелки (в положительном
направлении).
Условие независимости криволинейного интеграла от пути интегрирования.
Лемма.
Для того, чтобы
криволинейный интеграл
 не
зависел от
пути интегрирования (зависел
только от начальной и конечной точки),
необходимо
и достаточно, чтобы
этот интеграл,
взятый по
любому замкнутому контуру был
равен
не
зависел от
пути интегрирования (зависел
только от начальной и конечной точки),
необходимо
и достаточно, чтобы
этот интеграл,
взятый по
любому замкнутому контуру был
равен
 .
.
Теорема.Если
функции
и
непрерывны
вместе со своими частными производными
в односвязной области
,
то для того, чтобы криволинейный
интеграл
не
зависел от линии интегрирования, лежащей
в области
,
необходимо
и достаточно, чтобы
во всех точках области
выполнялось
равенство
 .
.
Четыре равносильных утверждения для функций
1.
Криволинейный интеграл
по
любому к пути равен
 2.
Криволинейный
интеграл
не зависит
от линии интегрирования.
2.
Криволинейный
интеграл
не зависит
от линии интегрирования.
