1.2. Метод Гаусса с выбором главного элемента

Современные исследования, относящиеся к гауссову исключению, вскрыли важность двух идей: необходимости выбора главного элемента и правильной интерпретации ошибок округления.

Метод Гаусса с выбором главного элемента (метод главных элементов) заключается в том, что при прямом ходе производится выбор наибольшего по модулю (главного) из всех элементов рассматриваемого столбца. Такая процедура называется выбором главного элемента столбца.

Последнее исключает деление на ноль, если матрица содержит нулевые элементы, и повышает точность вычислений при наличии ошибок округления.

Количество арифметических операций в методе Гаусса связано с размерностью системы и примерно равно . В методе Гаусса с выбором главного элемента погрешность округления обычно невелика. Только для плохо обусловленных систем устойчивость этого метода оказывается недостаточной.

Погрешность округления можно ещё уменьшить, если выбирать в каждом цикле элемент, максимальный по модулю во всей матрице. Однако точность при этом возрастает не сильно по сравнению со случаем выбора главного элемента, а расчёт заметно усложняется, ибо требуется перестановка не только строк, но и столбцов.

Контроль полученных решений можно провести путем их подстановки в исходную СЛАУ и вычисления невязок r _k , разностей между правыми и левыми частями уравнений:

При малой погрешности решений величины r _k будут близки к нулю.

Пример 1.2

{Прямой ход исключения переменных}

For k:= 1 to N do

begin

S:= a[k,k];

J:= k;

{Выбор главного элемента}

For I:= k+1 to N do

begin

R:= a[i,k];

If Abs(R) > Abs(S) then

begin

S:= R;

J:= i;

end;

end;

If S = 0.0 then Exit;

{Перестановка уравнений}

If j<>k then For I:= k to N do

begin

R:= a[k,i];

a[k,i]:= a[j,i];

a[j,i]:= R;

end;

R:= b[k];

b[k]:= b[j];

b[j]:= R;

{Продолжение прямого хода}

For j:= k+1 to N do a[k,j]:= a[k,j]/S;

b[k]:= b[k]/S;

For i:= k+1 to N do

begin

R:= a[j,k];

For j:= k+1 to N do a[i,j]:= a[i,j] - a[k,j]*R;

b[i]:= b[i] – b[k]*R;

end;

end;

{Обратный ход: последовательное нахождение корней }

If S <> 0.0 then

For i:= N Downto 1 do

begin

S:= b[i];

For j:= i+1 to N do S:= S – x[j]*a[i,j];

x[i]:= S;

end;

При реализации данного метода требуется:

• выполнить 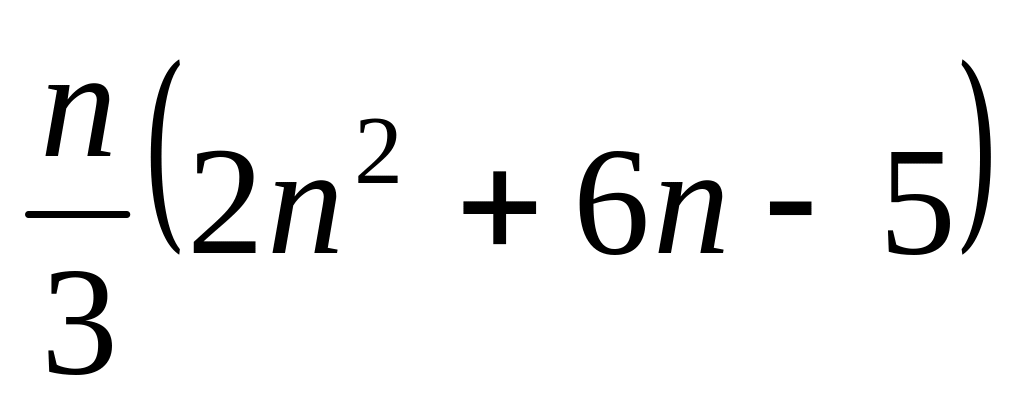арифметических операций, в том числе умножений и делений;

• одновременно запоминать 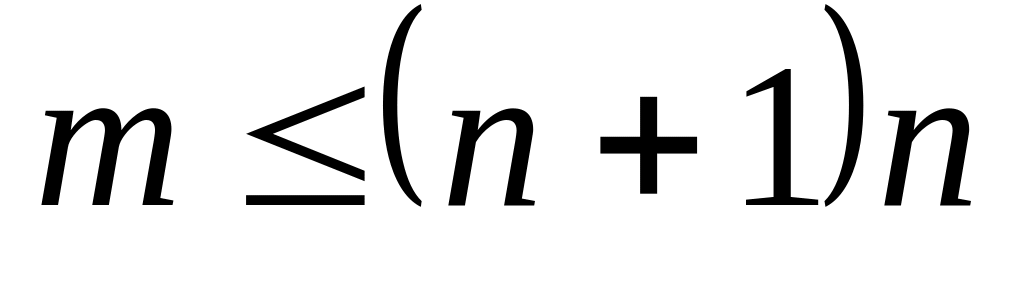промежуточных результатов.

Метод главных элементов целесообразно применять в тех случаях, когда:

• коэффициенты системы являются дробными числами;

• решение должно быть получено с минимальной погрешностью;

• порядок системы , а также когда необходимо решить систему высокого порядка, у которой матрица коэффициентов имеет подавляющее количество нулевых элементов.

К недостаткам этого метода следует отнести громоздкость вычислительной схемы и сложность программирования.

2. Метод Ньютона для снау

Название метод Ньютона применяется к целому семейству методов, для которых собственно метод Ньютона служит базовым прототипом.

Рассмотрим простой пример.

Поскольку , где -начальное приближение, то

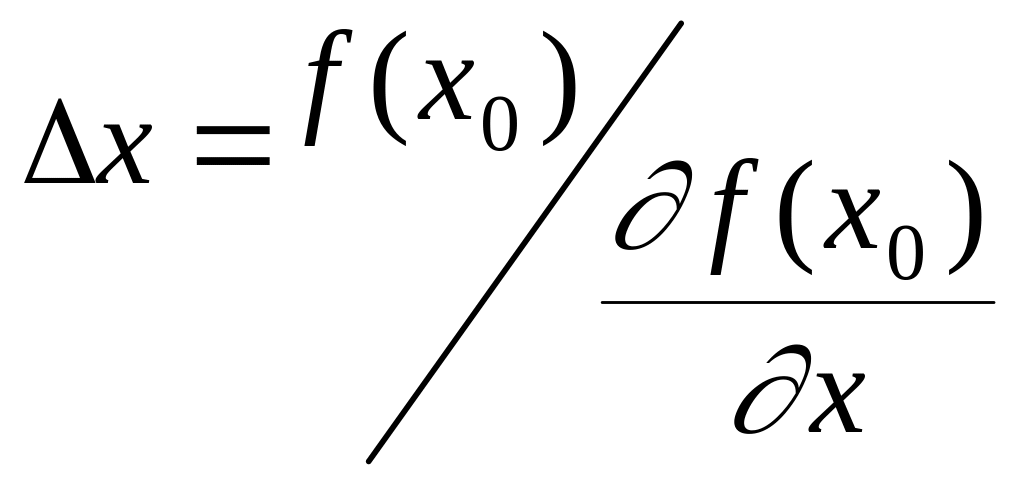
и можно получить новое приближение . Продолжая итерационный процесс можно с требуемой точностью приблизиться к одному из решений, например,

Расчетная формула для метода Ньютона может быть получена, если представить в окрестности текущего приближения в виде ряда Тейлора

,

и ограничиться линейными членами, тогда в матричной форме получим

,

где

Рис. 0. Итерация метода Ньютона для .