
- •Содержание
- •3.1. Аппроксимация данных методом наименьших квадратов 11
- •1. Решение систем линейных алгебраических уравнений
- •1.1. Классический метод Гаусса
- •1.2. Метод Гаусса с выбором главного элемента
- •2. Метод Ньютона для снау
- •2.1. Вариант 1
- •2.2. Вариант 2
- •I, n : IntType;
- •X,y,x0,y0 : RealType;
- •3. Аппроксимация данных методом наименьших квадратов
- •3.1. Аппроксимация данных методом наименьших квадратов
- •3.2. Аппроксимация данных с другими нормами
- •3.3. Аппроксимация данных многочленом заданной степени
- •Var X,y:array[1..Nmax] of real;
- •I,n:integer;
- •4. Решение систем дифференциальных уравнений
- •4.1. Метод Эйлера
- •4.2. Методы Рунге-Кутта
- •Проверка выполнения программы
- •X, h: RealType;
- •I, j : IntType;
- •X : RealType;
- •I, j, k : IntType;
2.1. Вариант 1
Применительно
к СНАУ
![]() получим следующий алгоритм:
получим следующий алгоритм:
1.
Выбрать начальный вектор
![]() ,
положить
,
положить
![]()
2.
Вычислить вектор
![]() .
Если все
.
Если все
![]() ,
где e-
заданная точность расчета, то получено
решение, расчет окончен. Если
,
где e-
заданная точность расчета, то получено
решение, расчет окончен. Если
![]() и
и
![]() ,
то итерационный процесс расходится,
расчет завершить аварийно.
,
то итерационный процесс расходится,
расчет завершить аварийно.
3. Построить матрицу Якоби
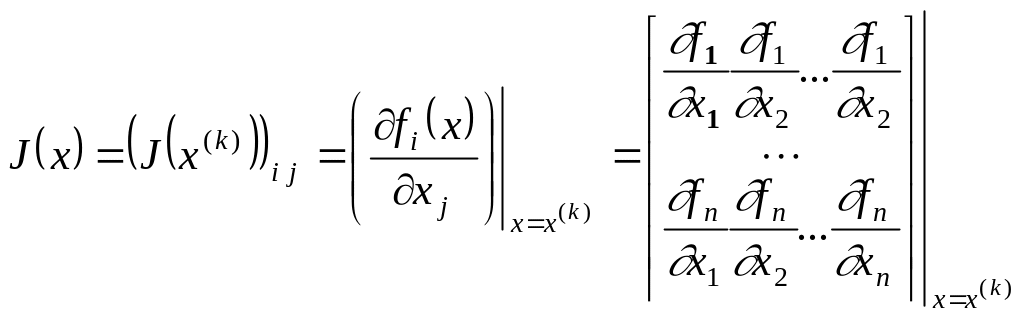
и
вычислить значения всех производных в
точке
![]() .
.
4.
Решить систему уравнений, определив
вектор
поправок
![]()
![]()
5. Вычислить новое приближение
![]()
и
положить
![]() .
.
6.
Если
![]() ,
где
,
где
![]() -заданное
предельное число итераций, то аварийно
завершить расчет, иначе перейти к п.2
алгоритма.
-заданное
предельное число итераций, то аварийно
завершить расчет, иначе перейти к п.2
алгоритма.
7. Конец алгоритма.
Метод Ньютона при начальном приближении близком к некоторому решению часто обладает устойчивой квадратичной сходимостью. При плохой начальной точке имеет место расходящийся итерационный процесс. Метод Ньютона расходится, если матрица Якоби плохо обусловлена в окрестности решения. Часто перед использованием метода Ньютона выполняют несколько итераций, например, методом последовательных приближений для того, чтобы иметь «хорошее» начальное приближение.
В качестве косвенного критерия расхождения итерационного процесса можно использовать изменение знака Якобиана - определителя матрицы Якоби. Однако это условие, являясь достаточным, не является необходимым. Якобиан может быть вычислен, как побочный продукт решения методом Гаусса системы из п.3 алгоритма.
2.2. Вариант 2
Алгоритм:
Задаём абсолютную или относительную погрешность
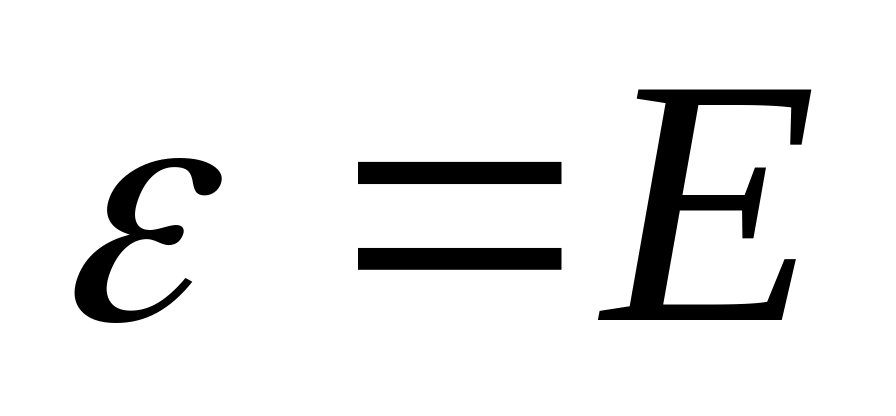 ,
число уравнений
,
число уравнений
 ,
максимальное число итераций
,
максимальное число итераций
 и вектор начальных приближений
и вектор начальных приближений
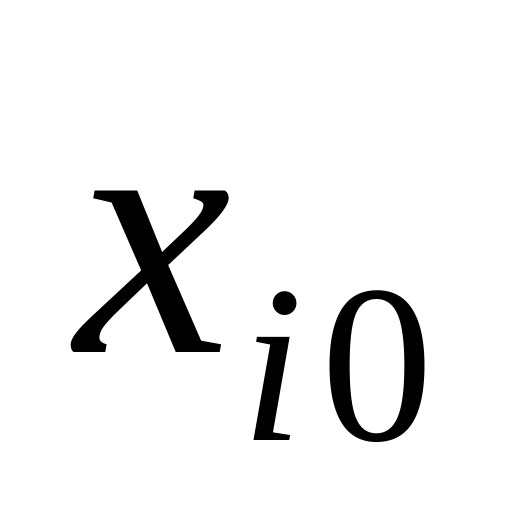 (с компонентами
(с компонентами
 ).
).Используя разложение
 в ряд Тейлора, формулируем матрицу
Якоби
в ряд Тейлора, формулируем матрицу
Якоби
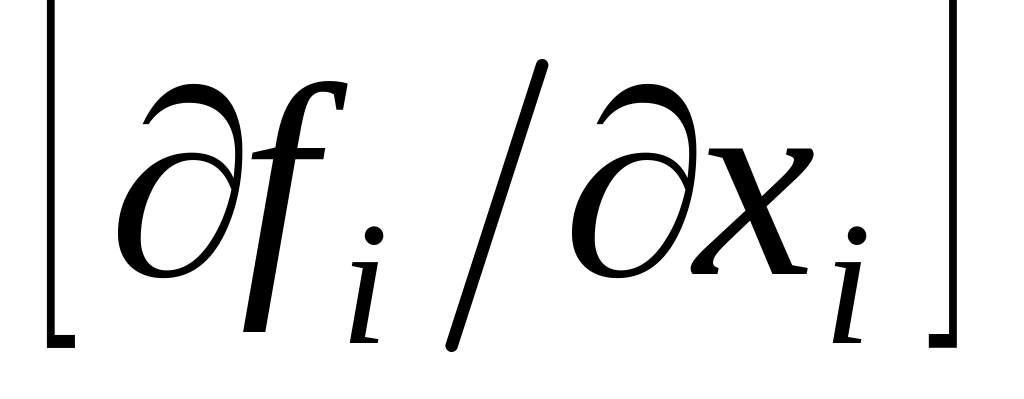 ,
необходимую для расчёта приращений
при малом изменении переменных. Матрица
Якоби в развёрнутом виде записывается
следующим образом:
,
необходимую для расчёта приращений
при малом изменении переменных. Матрица
Якоби в развёрнутом виде записывается
следующим образом:
![]()
Поскольку
аналитическое дифференцирование
![]() в общем случае нежелательно, заменяем
частные производные в матрице Якоби их
приближенными конечно-разностными
значениями
в общем случае нежелательно, заменяем
частные производные в матрице Якоби их
приближенными конечно-разностными
значениями
![]()
где
![]() - малое приращение
- малое приращение
![]() ,
например
,
например
![]() .
.
Составляем и решаем систему линейных уравнений для малых приращений :
![]()
Решение
этой системы даёт
![]() ,
т. е.
,
т. е.
![]() .
.
Вычисляем уточнённые значения
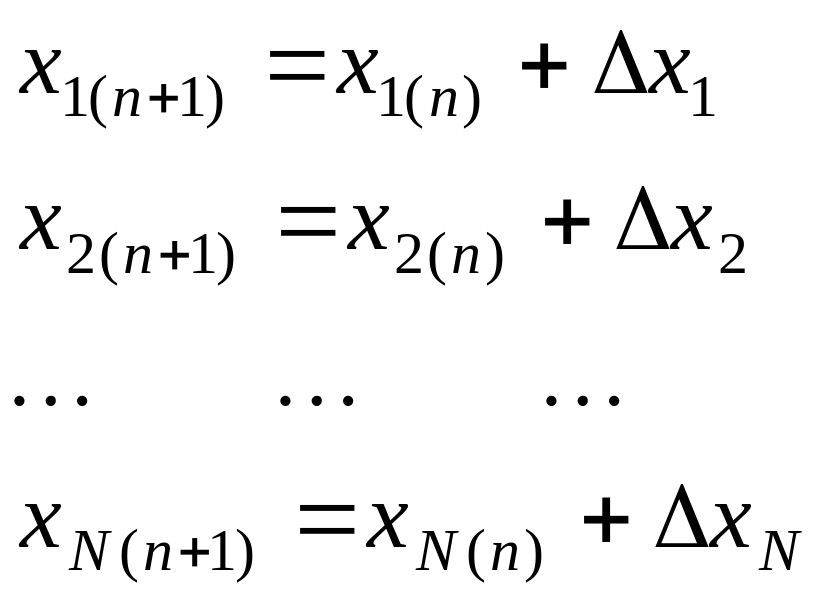
или в общем виде
![]()
Для всех проверяем одно из условий:
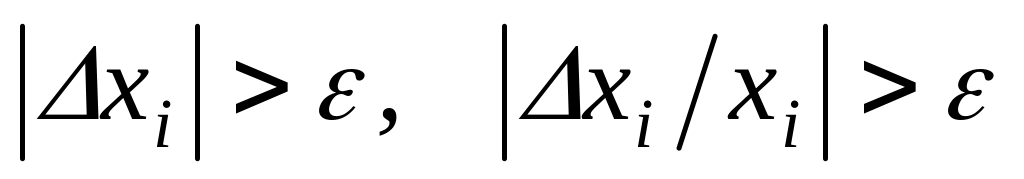 по абсолютной и относительной
погрешностям.
по абсолютной и относительной
погрешностям.
Если
оно выполняется, идём к п. 2, т. е. выполняем
новую итерацию. Иначе считаем вектор
![]() найденным решением.
найденным решением.
Пример решения 1.
Испытаем метод Ньютона на примере
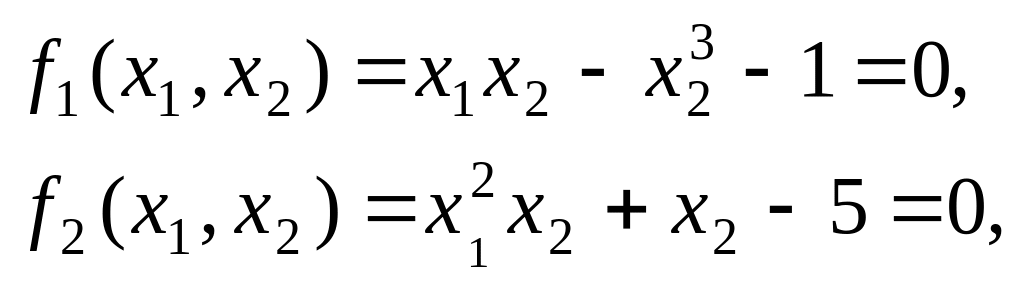
с
![]() .
Матрица Якоби имеет вид
.
Матрица Якоби имеет вид
![]() ,
,
и уравнение Ньютона имеет вид
![]()
Использование
гауссова исключения даёт
![]() ,
и поэтому новым приближением к решению
будет
,
и поэтому новым приближением к решению
будет
![]() .
Решением же системы нелинейных уравнений
является
.
Решением же системы нелинейных уравнений
является
![]() .
.
Пример программы 2.
{$N+}
Program Newton;
{Решение систем нелинейных алгебраических уравнений методом Ньютона}
Uses Crt;
Type
IntType = Integer; {Целый тип данных}
RealType = Extended; {Вещественный тип данных}
ArrayType = Array[1..2] of RealType; {Массив вещественного типа}
MatrixType = Array[1..2,1..2] of RealType; {Матрица вещественного типа}
BoolType = Boolean;
Const
NameOut = 'D:\FORTRAN\PRAC_F77\Var-Uru\NEWTON\newton-p.out';
Eps= 0.1E-6;
A = 9.0;
B = 10.0;
C = 3.2;
D = 0.3;
E = -3.0;
Var
