- •Содержание
- •3.1. Аппроксимация данных методом наименьших квадратов 11
- •1. Решение систем линейных алгебраических уравнений
- •1.1. Классический метод Гаусса
- •1.2. Метод Гаусса с выбором главного элемента
- •2. Метод Ньютона для снау
- •2.1. Вариант 1
- •2.2. Вариант 2
- •I, n : IntType;
- •X,y,x0,y0 : RealType;
- •3. Аппроксимация данных методом наименьших квадратов
- •3.1. Аппроксимация данных методом наименьших квадратов
- •3.2. Аппроксимация данных с другими нормами
- •3.3. Аппроксимация данных многочленом заданной степени
- •Var X,y:array[1..Nmax] of real;
- •I,n:integer;
- •4. Решение систем дифференциальных уравнений
- •4.1. Метод Эйлера
- •4.2. Методы Рунге-Кутта
- •Проверка выполнения программы
- •X, h: RealType;
- •I, j : IntType;
- •X : RealType;
- •I, j, k : IntType;
4.2. Методы Рунге-Кутта
Для
уменьшения погрешности метода
интегрирования ОДУ, использующего
разложение искомого решения в ряд
Тейлора (5), необходимо учитывать большее
количество членов ряда. Однако при этом
возникает необходимость аппроксимации
производных от правых частей ОДУ.
Основная идея методов Рунге-Кутта
заключается в том, что производные
аппроксимируются через значения функции
![]() в точках на интервале
в точках на интервале
![]() ,
которые выбираются из условия наибольшей
близости алгоритма к ряду Тейлора. В
зависимости от старшей степени h,
с которой учитываются члены ряда,
построены вычислительные схемы
Рунге-Кутта разных порядков точности.
Так, например, для второго порядка
получено однопараметрическое семейство
схем вида
,
которые выбираются из условия наибольшей
близости алгоритма к ряду Тейлора. В
зависимости от старшей степени h,
с которой учитываются члены ряда,
построены вычислительные схемы
Рунге-Кутта разных порядков точности.
Так, например, для второго порядка
получено однопараметрическое семейство
схем вида
![]() ,
(10)
,
(10)
где![]() - свободный параметр,
- свободный параметр,
![]() .
.
Локальная погрешность схем (10) имеет третий порядок, глобальная - второй; т.е. решение ОДУ, полученное по этой схеме, равномерно сходится к точному решению с погрешностью .
Для
параметра
![]() наиболее
часто используются значения
наиболее
часто используются значения
![]() .
В первом случае формула (10) приобретает
вид
.
В первом случае формула (10) приобретает
вид
![]() ,
,
здесь
при прогнозе определяется методом
Эйлера решение в точке![]() .
.
Во
втором случае при
![]() от формулы (10) переходим к схеме
от формулы (10) переходим к схеме
![]() ,
,
здесь
при прогнозе определяется методом
Эйлера решение в точке
![]() .
.
Метод Рунге-Кутта второго порядка называют методом Эйлера-Коши.
Для построения вычислительных схем методов Рунге-Кутта четвертого порядка (классического) в тейлоровском разложении искомого решения y(x) учитываются члены, содержащие степени шага h до четвертого порядка включительно. После аппроксимации производных правой части ОДУ получено семейство схем Рунге-Кутта четвертого порядка, из которых наиболее используемой в вычислительной практике является следующая:
![]() ,
,
где
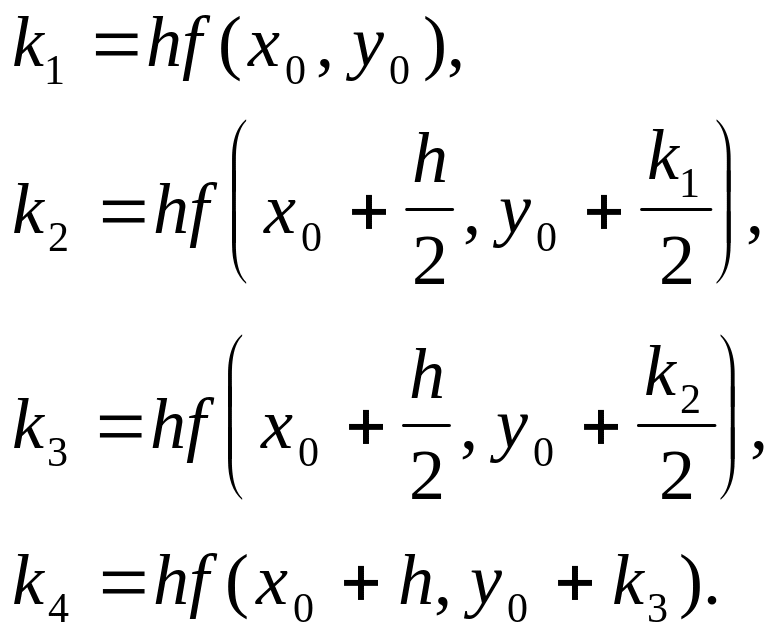
Вычислительная схема метода Рунге-Кутта пятого порядка имеет вид
![]() ,
,
где
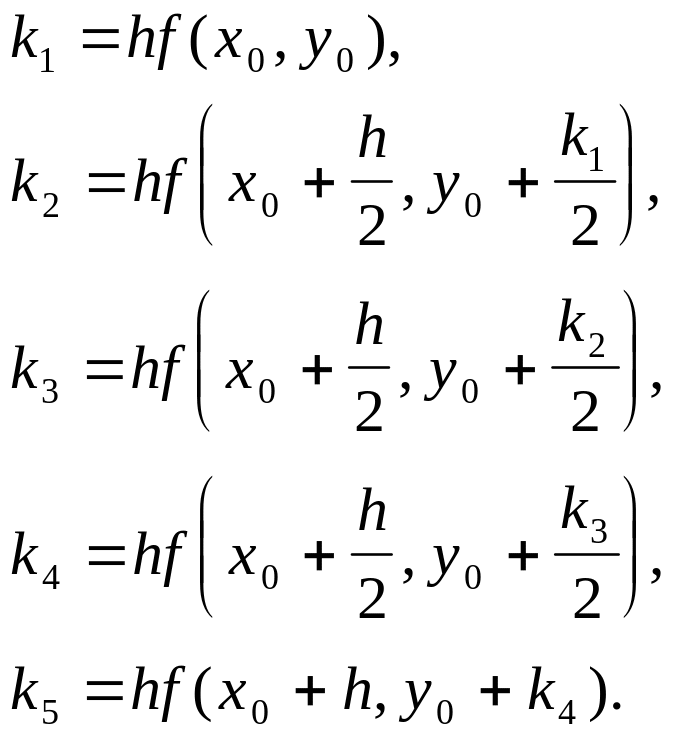
Мерсон предложил модификацию метода Рунге-Кутта четвертого порядка, позволяющую оценивать погрешность на каждом шаге и принимать решение об изменении шага. Схема Мерсона в виде, удобном для программирования, выглядит следующим образом:
![]() ,
(11)
,
(11)
где
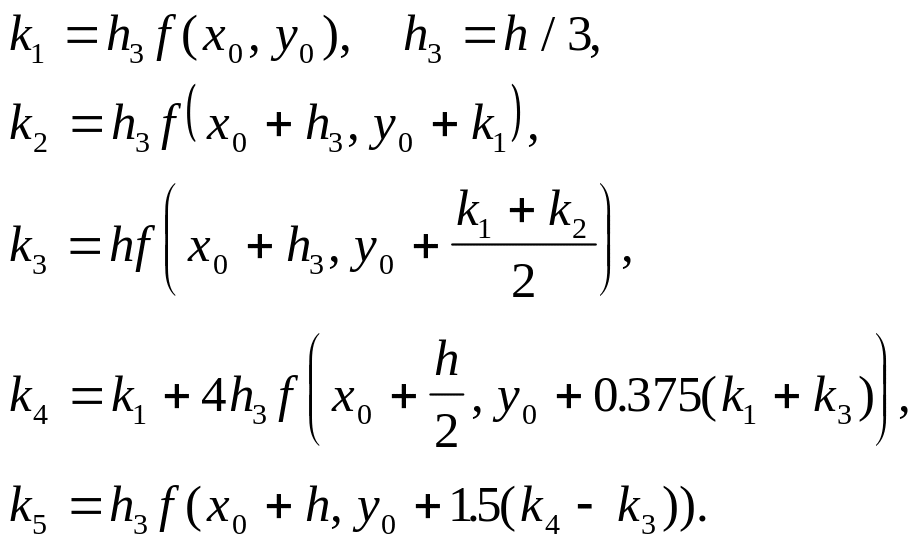
Схема Мерсона требует на каждом шаге вычислять правую часть ОДУ в пяти точках, но за счет только одного дополнительного коэффициента по сравнению с классической схемой Рунге-Кутта на каждом шаге можно определить погрешность решения по формуле
![]() .
(12)
.
(12)
Для
автоматического выбора шага интегрирования
рекомендуется следующий критерий. Если
абсолютное значение величины R,
вычисленное по формуле (12), окажется
больше допустимой заданной погрешности
![]() :
:
![]() ,
,
то шаг h уменьшается в два раза и вычисления по схеме (11) повторяются с точки (x0,y0). При выполнении условия
![]()
шаг h можно удвоить.
Автоматический выбор шага позволяет значительно сократить время решения ОДУ.