
- •25. Некоторые законы распределения непрерывных случайных величин: экспоненциальное распределение.
- •26. Некоторые законы распределения непрерывных случайных величин: нормальное распределение.
- •27. Неравенство Чебышева. Теорема Чебышева (закон больших чисел).
- •2. В случае, когда величина непрерывна, доказательство проводится аналогичным образом с заменой вероятностей элементом вероятности, а конечных сумм - интегралами. Действительно,
- •Формулировка теоремы Чебышева
Формулировка теоремы Чебышева
Если дисперсии независимых случайных величин ограничены одной и той же постоянной С, то, как бы мало не было данное положительное число Е, вероятность того, что отклонение средней арифметической этих случайных величин от средней арифметической их математических ожиданий а1, а2, …, аn не превзойдет по абсолютной величине Е, как угодно близка к единице, если число случайных величин достаточно велико.
Следствие.
Если независимые случайные величины имеют одинаковые, равные , математические ожидания, дисперсии их ограничены одной и той же постоянной С, а число случайных величин достаточно велико, то, сколько мало ни было данное положительное число Е, как угодно близка к единице вероятность того, что отклонение средней арифметической этих случайных величин от а не превзойдет по абсолютной величине Е.
При доказательстве теоремы Чебышева и следствия из нее с помощью неравенства Чебышева получаем такие оценки:
![]() , (63)
, (63)
![]() .
.
Предварительно решим следующую вспомогательную задачу.
Имеется случайная
величина
с
математическим ожиданием
и
дисперсией
.
Над этой величиной производится ![]() независимых
опытов и вычисляется среднее арифметическое
всех наблюденных значений величины
.
Требуется найти числовые характеристики
этого среднего арифметического -
математическое ожидание и дисперсию -
и выяснить, как они изменяются с
увеличением
.
независимых
опытов и вычисляется среднее арифметическое
всех наблюденных значений величины
.
Требуется найти числовые характеристики
этого среднего арифметического -
математическое ожидание и дисперсию -
и выяснить, как они изменяются с
увеличением
.
Обозначим:
![]() -
значение величины
в
первом опыте;
-
значение величины
в
первом опыте;
![]() -
значение величины
во
втором опыте, и т. д.
-
значение величины
во
втором опыте, и т. д.
Очевидно,
совокупность величин ![]() представляет
собой
независимых
случайных величин, каждая из которых
распределена по тому же закону, что и
сама величина
.
Рассмотрим среднее арифметическое этих
величин:
представляет
собой
независимых
случайных величин, каждая из которых
распределена по тому же закону, что и
сама величина
.
Рассмотрим среднее арифметическое этих
величин:
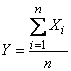 .
.
Случайная
величина ![]() есть
линейная функция независимых случайных
величин
.
Найдем математическое ожидание и
дисперсию этой величины. Согласно
правилам
есть
линейная функция независимых случайных
величин
.
Найдем математическое ожидание и
дисперсию этой величины. Согласно
правилам ![]() 10
для определении числовых характеристик
линейных функций получим:
10
для определении числовых характеристик
линейных функций получим:
 ;
;
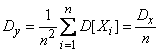 .
.
Итак, математическое ожидание величины не зависит от числа опытов и равно математическому ожиданию наблюдаемой величины ; что касается дисперсии величины , то она неограниченно убывает с увеличением числа опытов и при достаточно большом может быть сделана сколь угодно малой. Мы убеждаемся, что среднее арифметическое есть случайная величина со сколь угодно малой дисперсией и при большом числе опытов ведет себя почти как не случайная.
Теорема Чебышева и устанавливает в точной количественной форме это свойство устойчивости среднего арифметического. Она формулируется следующим образом:
При достаточно большом числе независимых опытов среднее арифметическое наблюденных значении случайной величины сходится по вероятности к ее математическому ожиданию.
Запишем теорему
Чебышева в виде формулы. Для этого
напомним смысл термина «сходится по
вероятности». Говорят, что случайная
величина ![]() сходится
по вероятности к величине
,
если при увеличении
вероятность
того, что
и
будут
сколь угодно близки, неограниченно
приближается к единице, а это значит,
что при достаточно большом
сходится
по вероятности к величине
,
если при увеличении
вероятность
того, что
и
будут
сколь угодно близки, неограниченно
приближается к единице, а это значит,
что при достаточно большом
![]() ,
,
где ![]() -
произвольно малые положительные числа.
-
произвольно малые положительные числа.
Запишем в
аналогичной форме теорему Чебышева.
Она утверждает, что при увеличении
среднее
арифметическое ![]() сходится
по вероятности к
,
т. е.
сходится
по вероятности к
,
т. е.
 .
(13.3.1)
.
(13.3.1)
Докажем это неравенство.
Доказательство. Выше было показано, что величина
имеет числовые характеристики
![]() ;
; ![]() .
.
Применим к
случайной величине
неравенство
Чебышева, полагая ![]() :
:
![]() .
.
Как бы мало ни
было число ![]() ,
можно взять
таким
большим, чтобы выполнялось неравенство
,
можно взять
таким
большим, чтобы выполнялось неравенство
![]()
где ![]() -
сколь угодно малое число.
-
сколь угодно малое число.
Тогда
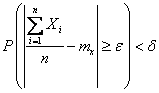 ,
,
откуда, переходя к противоположному событию, имеем:
 ,
,
что и требовалось доказать.
