4.1. Понятие определенного интеграла

Перед тем как приступить непосредственно к рассмотрению методов численного интегрирования, рассмотрим теоретические основы, приводящие к понятию определенного интеграла. Пусть на отрезке задана функция . Разобьем отрезок на отрезков точками , , …, следующим образом , причем , а . На каждом отрезке , , выберем некоторую точку ; обозначим длину данного отрезка через . Сумму вида будем называть интегральной суммой для функции на отрезке . Очевидно, что интегральная сумма зависит как от способа разбиения отрезка точками , , …, , так и от выбора точек , , …, на каждом из отрезков разбиения , .

Пусть функция неотрицательна на , тогда отдельное слагаемое интегральной суммы равно площади прямоугольника со сторонами и , . В результате значение интегральной суммы равно суммарной площади под кусочной линией, образованной на каждом из отрезков соответствующей прямой , параллельной оси абсцисс, рис. 4.1. Для выбранного разбиения отрезка обозначим через максимальную из длин отрезков , («диаметр разбиения»).

Рис. 4.1. Графическая иллюстрация интегральной суммы.

Определение 4.1. Пусть предел интегральной суммы при существует, конечен и не зависит от способа выбора точек , , …, , а также , , …, . Тогда этот предел называется определенным интегралом от функции на отрезке , обозначается , а сама функция называется интегрируемой на отрезке , то есть

.

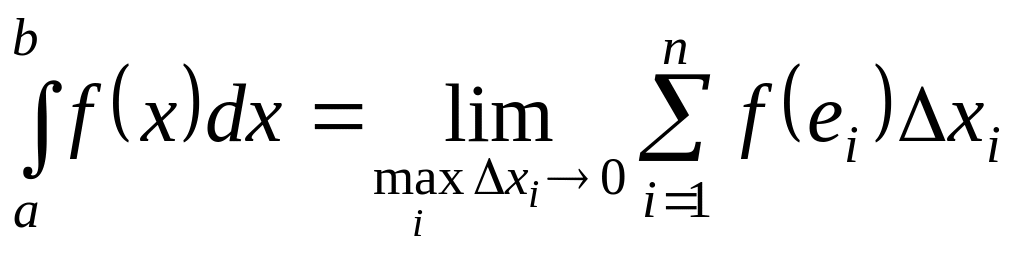С геометрической точки зрения значением определенного интеграла является площадь криволинейной трапеции – фигуры, ограниченной графиком функции и прямыми , и (рис. 4.2).

Рис. 4.2. Геометрическая интерпритация определенного интеграла.

Рассмотрим общий подход к решению задачи вычисления определенного интеграла. Введем в рассмотрение некоторую ломаную, которая расположена достаточно близко к кривой на отрезке , рис. 4.3.

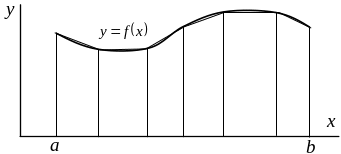
Рис. 4.3. Ломаная линия в геометрической интерпритации определенного интеграла.

Фигура под ломаной состоит из элементарных геометрических фигур (трапеций и прямоугольников), площадь которых может быть вычислена с помощью формул планиметрии. Поскольку ломаная выбрана достаточно близко к кривой , то суммарная площадь фигур под ней и значение соответствующего интеграла приближенно равны. Данное равенство оказывается тем более точным, чем ближе расположена ломаная к исходной кривой. Приведенные рассуждения носят качественный характер, для их использования на практике необходимо уточнить то, что описано нестрого: процедуру выбора ломаной и последующий переход к пределу.

В общем случае при реализации численных алгоритмов вычисления определенных интегралов от некоторой функции на отрезке полагаем, что на выбрана система точек и . Формулы такого вида называются квадратурными, коэффициенты и точки , , выбираются так, чтобы минимизировать погрешность вычисления интеграла.

4.2. Классификация методов численного интегрирования

Пусть рассматривается задача вычисления определенного интеграла вида

,

где – непрерывная и неотрицательная на отрезке функция, – верхний и нижний пределы интегрирования.

Во многих случаях, когда подынтегральная функция задана в аналитическом виде, определенный интеграл удается вычислить непосредственно с помощью формулы Ньютона-Лейбница как приращение первообразной функции на отрезке интегрирования:

,

где и – значения первообразной функции на концах отрезка интегрирования.

В реальных исследовательских задачах выразить интеграл через элементарные функции удается достаточно редко, а компактный и удобный для приведения к числу ответ получается еще реже. Поэтому на практике формулой Ньютона-Лейбница часто нельзя воспользоваться по двум основным причинам:

1. Вид функции не позволяет аналитически выразить первообразную через элементарные функции.

2. Подынтегральная функция задана таблично.

В этих случаях используют приближенные, численные методы интегрирования. Назначение большинства приближенных методов вычисления определенных интегралов состоит в замене подынтегральной функции аппроксимирующей функцией , для которой можно легко записать первообразную в элементарных функциях, то есть

,

где – погрешность вычисления интеграла.

Чаще всего функцию заменяют интерполяционным полиномом, для построения которого используются значения функции в узлах , :

,

где – остаточный член.

Подставляя полученное выражение в определенный интеграл вместо подынтегральной функции, получим общую формулу численного интегрирования

,

где – значения подынтегральной функции в узловых точках , – весовые коэффициенты, а – погрешность или остаточный член формулы.

Пояснение. Интерполяция – приближенное вычисление неизвестных значений функции по известным ее значениям в заданных точках. Наиболее простым является линейное интерполирование, при котором допускается, что приращение функции пропорционально приращению аргумента.

С целью уменьшения погрешности, связанной с заменой подынтегральной функции, отрезок интегрирования разбивают на отрезков и на каждом из полученных (частичных) отрезков , , заменяют подынтегральную функцию аппроксимирующей функцией . Тогда приближенное значение интеграла определяется суммой частичных интегралов от функций , взятых в пределах от до для :

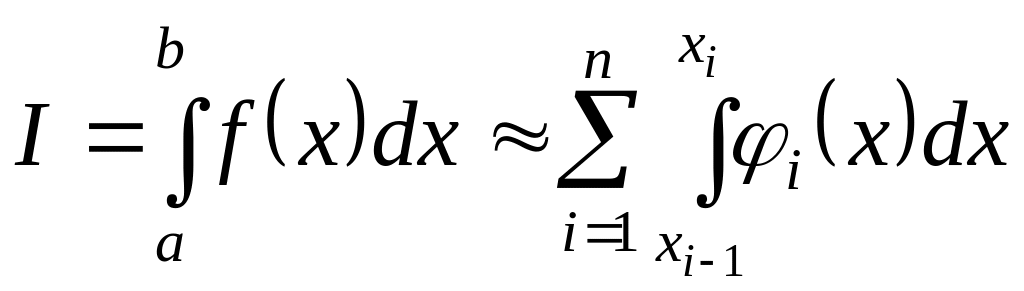. (4.1)

Методы численного интегрирования можно классифицировать в зависимости от способа аппроксимации подынтегральной функции с помощью функций , . В результате данной аппроксимации вычисление определенного интеграла реализуется посредством расчета суммарной площади элементарных геометрических фигур, составляющих соответствующую криволинейную трапецию с некоторой погрешностью. Рассмотрим краткую характеристику классов наиболее распространенных численных методов интегрирования.

Методы Ньютона-Котеса основаны на полиномиальной аппроксимации подынтегральной функции. Методы данного класса отличаются друг от друга степенью используемого полинома, от которой зависит количество узлов, в которых необходимо вычислять функцию . В методах Ньютона-Котеса отрезок интегрирования разбивается, как правило, на отрезки равной длины, величина которых определяется как и называется шагом интегрирования. Алгоритмы данных методов просты и легко поддаются программной реализации.

Сплайновые методы базируются на аппроксимации подынтегральной функции сплайнами и различаются по типу выбранных сплайнов. В данном учебно-методическом пособии эти методы рассматриваться не будут.

Пояснение. Под сплайном обычно понимают функцию, совпадающую с функциями более простой природы на каждом элементе разбиения своей области определения. Классический сплайн одной переменной строится следующим образом: область определения разбивается на конечное число отрезков, на каждом из которых сплайн совпадает с некоторым алгебраическим полиномом. Максимальная степень из использованных полиномов называется степенью сплайна. Математические сплайны берут свое начало от тонких гибких стержней, которыми пользовались чертежники для проведения плав­ных кривых через заданные точки. Стержень закреплялся в точках 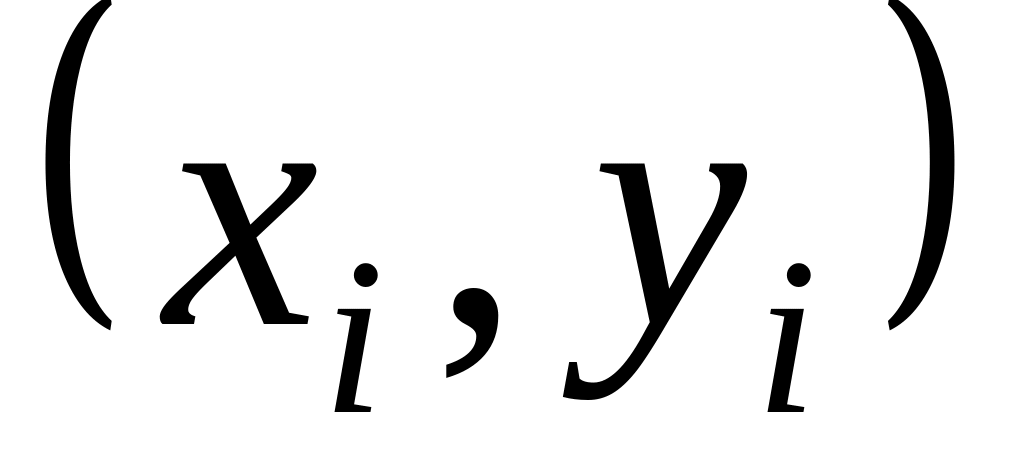, , и в результате подвешивания между ними грузов принимал форму кривой . Если перейти к математическому описанию сплайна, то сплайн-функцией степени с точками соединения будет функция , которая на отрезке имеет непрерывные производные до порядка включительно и на каждом из отрезков , , равна многочлену степени не выше .

Методы наивысшей алгебраической точности (например, методы Гаусса и Маркова) основаны на использовании заданного количества неравноотстоящих узлов, расположенных так, чтобы обеспечить минимальную погрешность интегрирования для наиболее сложных функций. Методы различаются способом выбора узлов и широко используются для интегрирования, в том числе они применимы и для вычисления несобственных интегралов (см. разд. 4.6). По сравнению с методами Ньютона-Котеса, методы наивысшей алгебраической точности более громоздки и требуют больших объемов оперативной памяти ЭВМ, в данном учебно-методическом пособии эти методы рассматриваться не будут.

В методах Монте-Карло узловые точки выбираются с помощью генератора случайных чисел, в результате для вычисления интеграла используется вероятностная процедура. Данные методы оказываются особенно эффективными при вычислении кратных интегралов.

Независимо от выбранного метода, в процессе численного интегрирования необходимо вычислить приближенное значение интеграла и оценить погрешность . Погрешность, возникающая при численном интегрировании (также как и при численном дифференцировании), имеет два основных источника. Первым источником погрешности является замена подынтегральной функции аппроксимирующей функцией – погрешность аппроксимации. Как будет показано далее, погрешность аппроксимации уменьшается с увеличением количества отрезков разбиения исходного отрезка интегрирования за счет более точной аппроксимации подынтегральной функции. Второй источник погрешности – неточности в вычислении подынтегральной функции в узловых точках и ошибки округления. Данная погрешность возрастает с ростом и с некоторого значения начинает преобладать над погрешностью аппроксимации. Это обстоятельство должно предостеречь от выбора чрезмерно большого числа .