§2. Способы задания графов
1. Перечислением (списком) вершин и рëбер (дуг).
2. Геометрическим способом. Граф может быть задан с помощью его диаграммы.
Пример 2.1. Пусть граф G = (S, U) задан списком вершин и рëбер:
S = {x1, x2, x3, x4, x5, x6},
U = {( x1, x2),( x1, x3),( x1, x6),( x2, x3),( x2, x5),( x3, x4),( x3, x5), (x3, x6), ( x4, x5)}. Тогда граф можно задать с помощью диаграммы, представленной на рис. 6.
3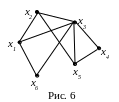
.
Матричным
способом. Этот
способ задания
используется
наиболее часто. Рассмотрим задание
графа матрицей смежности вершин, матрицей
смежности дуг, матрицей инциденций и
матрицей Кирхгофа.
Определение
2.1.
Матрицей
смежности вершин
графа G
= (S,
U)
порядка n
называется квадратная матрица P(G)
=
порядка n,
строки и столбцы которой соответствуют
вершинам графа, где элементы pij
равны
числу дуг, идущих из i-й
вершины в j-ю.
Для неорграфа матрица смежности вершин является симметричной относительно главной диагонали (см. замечание 1.1).
Определение
2.2.
Матрицей
смежности дуг
графа G
= (S,
U),
где
=
m,
называется квадратная матрица Q(G)
=
порядка m,
элементы qij
которой равны единице, если дуга ui
непосредственно
предшествует дуге uj,
и равны нулю в остальных случаях.
В случае неорграфа элемент qij равен единице, если ui и uj смежны, и нулю, если эти дуги не смежны.
Определение
2.3.
Матрицей
инциденций
мультиграфа G
= (S,
U),
где
=
n
и
=
m,
называется прямоугольная матрица R(G)
=
размерности n
m.
Элементы этой матрицы равны 1, если дуга
uj
исходит из i-й
вершины; –1, если дуга uj
входит
в i-ю
вершину; 0, если дуга uj
не инцидентна i-й
вершине.
Для неориентированного мультиграфа элемент равен единице, если вершина xi инцидентна ребру uj, и нулю, если вершина xi не инцидентна ребру uj.
Определение
2.4.
Матрицей
Кирхгофа
графа G
= (S,
U),
где = n,
называется матрица B(G)
=
порядка n,
где
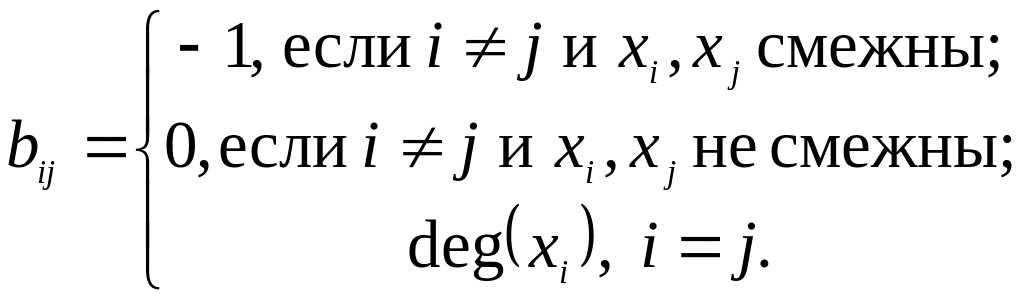
Очевидно, что сумма элементов в каждой строке и каждом столбце матрицы B(G) равна нулю. Кроме того, из этого следует, что алгебраические дополнения всех элементов матрицы Кирхгофа равны между собой.
Пример 2.2. Для графа G, изображëнного на рис. 7, составить матрицы смежности вершин, смежности дуг и инциденций.
Р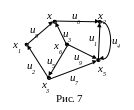
ешение.
Матрица
смежности вершин P(G):
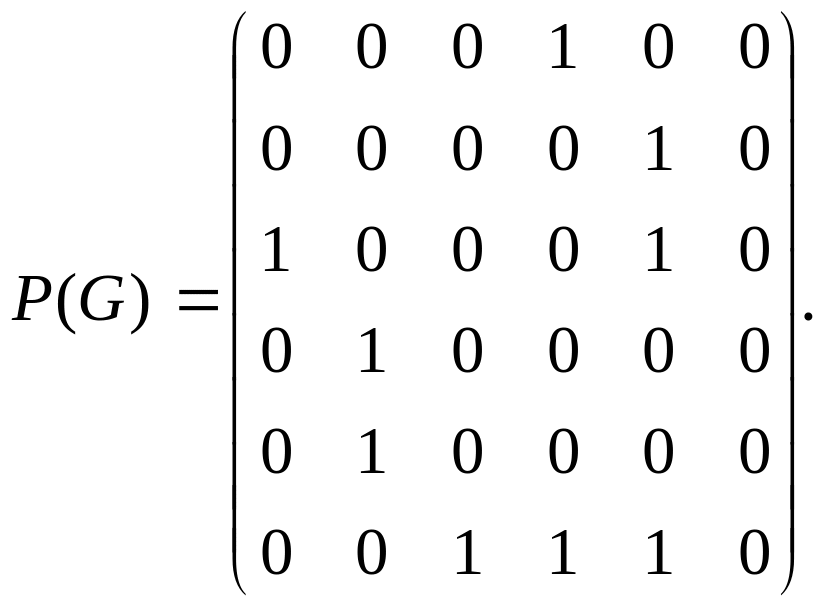
Матрица смежности дуг Q(G) и матрица инциденций R(G):
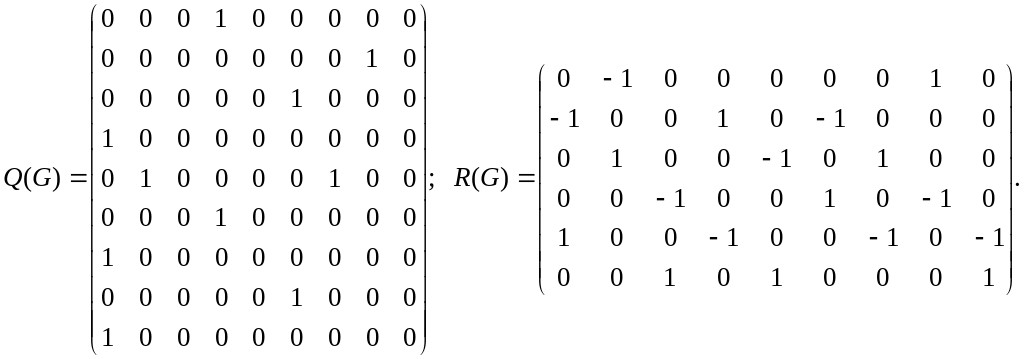
§3. Изоморфные графы
Определение 3.1. Графы G1 = (S1, U1) и G2 = (S2, U2) называются изоморфными (G1 G2), если между множествами их вершин S1 и S2 можно установить такое взаимно однозначное соответствие, при котором две произвольные вершины смежны в одном из графов тогда и только тогда, когда соответствующие им вершины смежны в другом графе. В случае орграфов ориентация дуг также должна быть одинаковой.
Очевидно, что отношение «быть изоморфными» на множестве всех графов является отношением эквивалентности. Следовательно, множество всех графов разбивается на классы попарно изоморфных графов.
З
амечание
3.1.
Диаграмма задает граф с точностью до
изоморфизма. Это означает, что все
различные диаграммы, содержащие одну
и ту же информацию о вершинах и ребрах
(дугах) графа и их взаимном расположении,
являются изображениями одного и того
же графа. Например, на рис. 8 представлено
изображение одного и того же графа.
Для того чтобы различать изоморфные графы, рассмотрим понятие помеченного графа.
Определение 3.2. Граф G порядка n называется помеченным, если его вершины занумерованы натуральными числами от 1 до n.
На рис. 9 изображены три разных помеченных графа порядка 3.
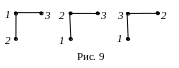Таким
образом, под непомеченым
(или абстрактным)
графом
следует понимать класс изоморфных
графов.
Замечание 3.2. Структура графа однозначно определяется его матрицей смежности вершин.
Теорема 3.1. Графы изоморфны тогда и только тогда, когда их матрицы смежности вершин получаются друг из друга в результате последовательности одновременных перестановок строк и столбцов (одновременно с перестановкой i-й и j-й строк переставляются i-й и j-й столбцы).
Из теоремы 3.1 следует, что ранги матриц смежности вершин изоморфных графов равны. Это позволяет ввести в рассмотрение следующее определение.
Определение 3.3. Рангом графа G (rank G) называется ранг его матрицы смежности вершин P(G).
Замечание 3.3. Структура мультиграфа однозначно определяется его матрицей инциденций.
Теорема 3.2. Мультиграфы изоморфны тогда и только тогда, когда их матрицы инциденций получаются друг из друга в результате последовательности произвольных перестановок строк и столбцов.