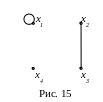- •Введение в теорию графов
- •Введение
- •§1. Основные понятия и определения
- •§2. Способы задания графов
- •§3. Изоморфные графы
- •§4. Взвешенные графы
- •§5. Подграф
- •§6. Операции над графами
- •§7. Маршруты, цепи, циклы
- •§8. Связность. Компоненты связности
- •§9. Метрические характеристики графа
- •§10. Деревья и их свойства. Лес
- •§11. Эйлеровы цепи и циклы
- •§12. Гамильтоновы цепи и циклы
- •§13. Планарные графы
- •§14. Раскраска графов. Хроматические графы
- •Список литературы
- •Введение в теорию графов
§8. Связность. Компоненты связности
Определение 8.1. Граф (орграф) называется связным (сильно связным), если для любых двух его различных вершин существует маршрут (путь), соединяющий вершины x и y (из x в y).
Говорят, что вершина y орграфа (графа) G достижима из вершины x, если либо y = x, либо существует путь из x в вершину y (маршрут, соединяющий вершины x и у).
Таким образом, орграф G является сильно связным, если любые две его вершины взаимно достижимы.
Определение 8.2. Неориентированным псевдографом, ассоциированным с ориентированным псевдографом G = (S, U), называется неориентированный
псевдограф F(G), полученный из G заменой всех ориентированных рëбер на неориентированные.
Определение 8.3. Орграф G называется слабо связным, если ассоциированный с ним неориентированный псевдограф F(G) является связным.
Определение 8.4. Граф (орграф) называется несвязным, если он не является связным (слабо связным).
П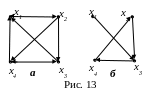 ример
8.1. На
рис. 13а
изображëн сильно связный орграф, а на
рис. 13б
– слабо связный орграф, т.к., например,
вершина x2
не достижима из вершины x1.
ример
8.1. На
рис. 13а
изображëн сильно связный орграф, а на
рис. 13б
– слабо связный орграф, т.к., например,
вершина x2
не достижима из вершины x1.
З
x2
x4
Определение 8.5. Всякий максимальный по включению (сильно) связный подграф данного графа называется его (сильной) связной компонентой, или (сильной) компонентой связности.
Утверждение 8.1. Пусть G = (S, U) – псевдограф с k компонентами связности:
G1 = (S1, U1), …, Gk = (Sk, Uk). Тогда
S = S1 … Sk, U = U1 …Uk, т.е. G = G1…Gk;
SiSj = , UiUj = при i j;
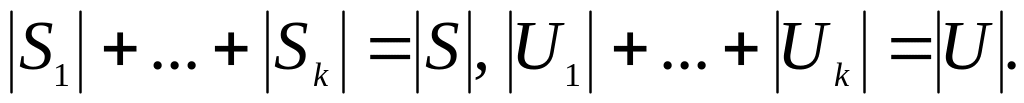
Утверждение 8.2. Пусть G = (S, U) – ориентированный псевдограф с k компонентами сильной связности: G1 = (S1,U1), …, Gk = (Sk, Uk). Тогда
S = S1 … Sk, U1 …Uk U;
SiSj = , UiUj = при i j;
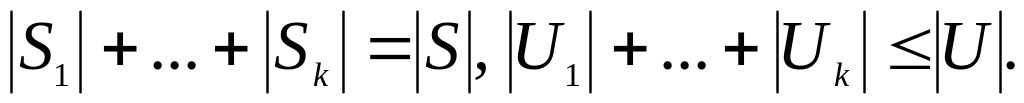
Рассмотрим задачи нахождения сильных компонент орграфа и всех маршрутов, состоящих из рëбер (дуг) графа.
Пусть P(G) – матрица смежности вершин орграфа G = (S, U) порядка n. Обозначим через матрицу B = (bij) квадратную матрицу порядка n, удовлетворяющую условию: B = E + P + P2 + …+ Pn.
Определение 8.6. Квадратная матрица C = (cij) порядка n, где
![]()
называется матрицей достижимости орграфа G.
Заметим, что элемент cij равен единице тогда и только тогда, когда в орграфе G существует путь из вершины xi в вершину xj.
Определение 8.7. Квадратная матрица L = (lij) порядка n, где
![]()
называется матрицей контрдостижимости орграфа G.
Известно, что L = CT. Матрицы С и L используются для нахождения сильных компонент связности графа.
Определение 8.8. Квадратная матрица F = (fij) порядка n, удовлетворяющая условию F = C L, где операция означает поэлементное произведение матриц C и L (т.е. fij = cij·lij для любых i и j), называется матрицей сильных компонент связности орграфа G.
Элемент fij матрицы F равен единице тогда и только тогда, когда вершины xi и xj взаимно достижимы. Таким образом, множество вершин некоторой сильной компоненты связности Gp = (Sp, Up) орграфа G = (S, U), кроме вершины xi, содержит также все вершины xj S, для которых fij = 1.
Для определения количества маршрутов с заданным количеством рëбер (дуг) графа используется следующая теорема.
Теорема
8.1. Пусть
P(G)
– матрица смежности вершин графа G
= (S,
U)
порядка n
и
![]() – k-я
степень матрицы P.
Тогда элемент матрицы Pk
равен
числу маршрутов, состоящих из k
ребер (дуг) графа G
из вершины xi
в вершину xj.
– k-я
степень матрицы P.
Тогда элемент матрицы Pk
равен
числу маршрутов, состоящих из k
ребер (дуг) графа G
из вершины xi
в вершину xj.
Пример 8.1. Найти сильные компоненты связности орграфа G, изображенного на рис. 14, и все маршруты длины три дуги, исходящие из вершины x1.
Р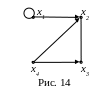 ешение.
Найдем матрицу смежности вершин
ешение.
Найдем матрицу смежности вершин
орграфа G:
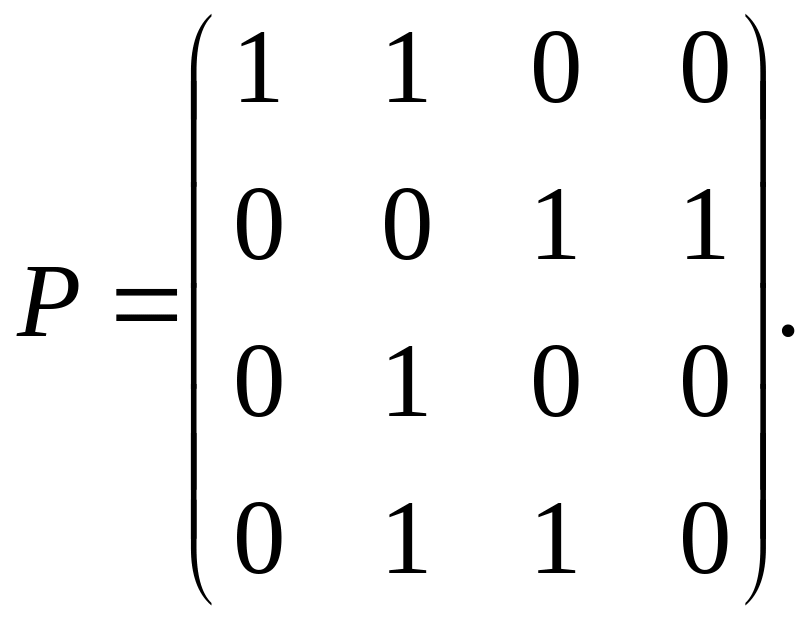 Так
как порядок орграфа G
равен
Так
как порядок орграфа G
равен
четырем, то для нахождения матрицы B вычислим Pk, где k = 1, 2, 3, 4:
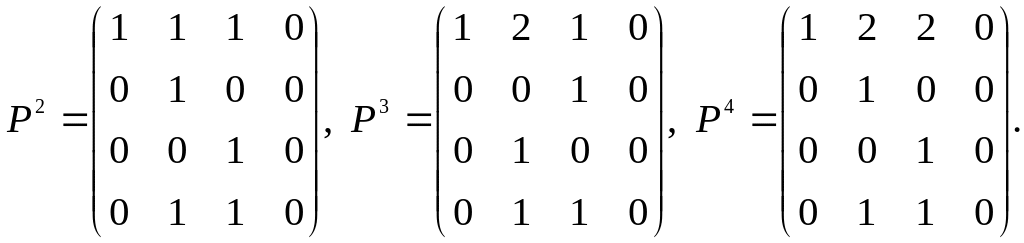
Следовательно,
B
= E
+ P
+ P2
+
P3
+
P4
=
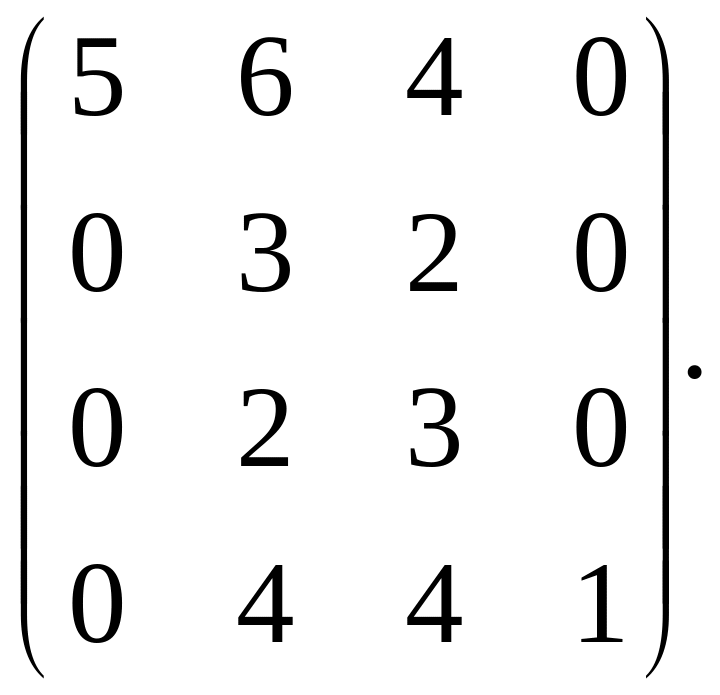 Найдем матрицы
Найдем матрицы
достижимости и контрдостижимости орграфа G:
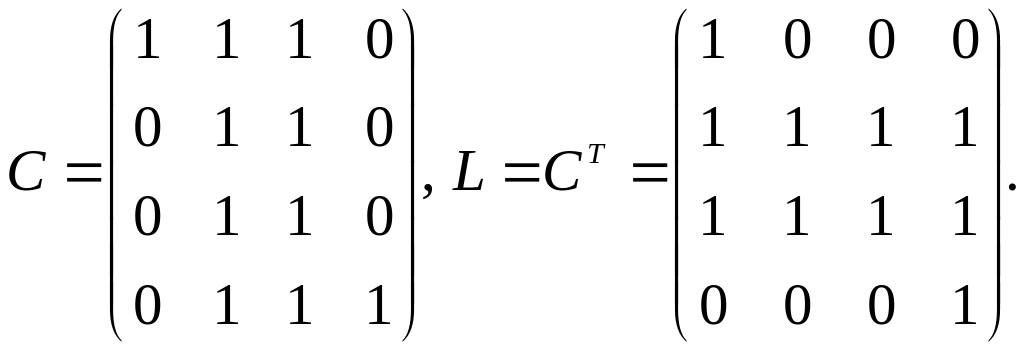 Отсюда
получаем матрицу
Отсюда
получаем матрицу
сильных
компонент связности орграфа G:
F
=
C
L
=
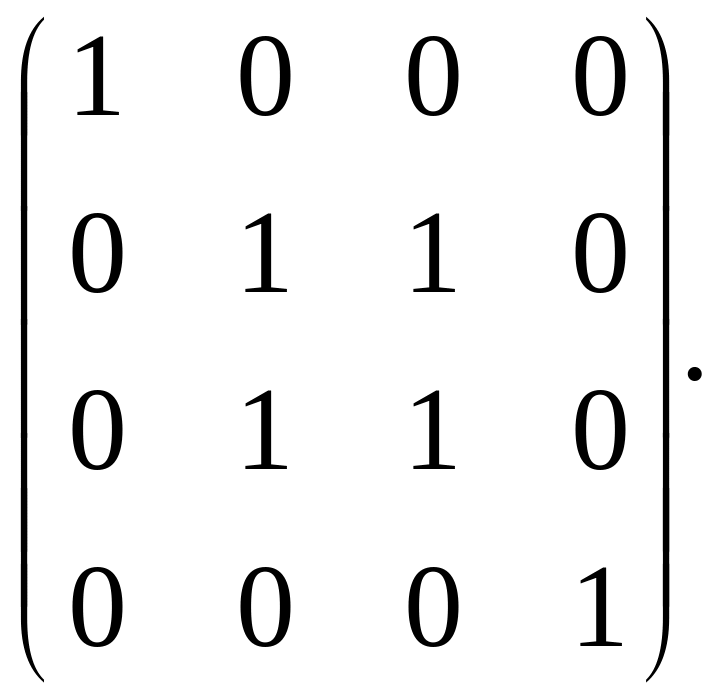
Таким образом, данный орграф G содержит три сильные компоненты связности G1 = (S1, U1), G2 = (S2, U2) и G3 = (S3, U3), где S1 = {x1}, S2 = {x2, x3},
S3 = {x4}, диаграммы которых изображенные на рис. 15.