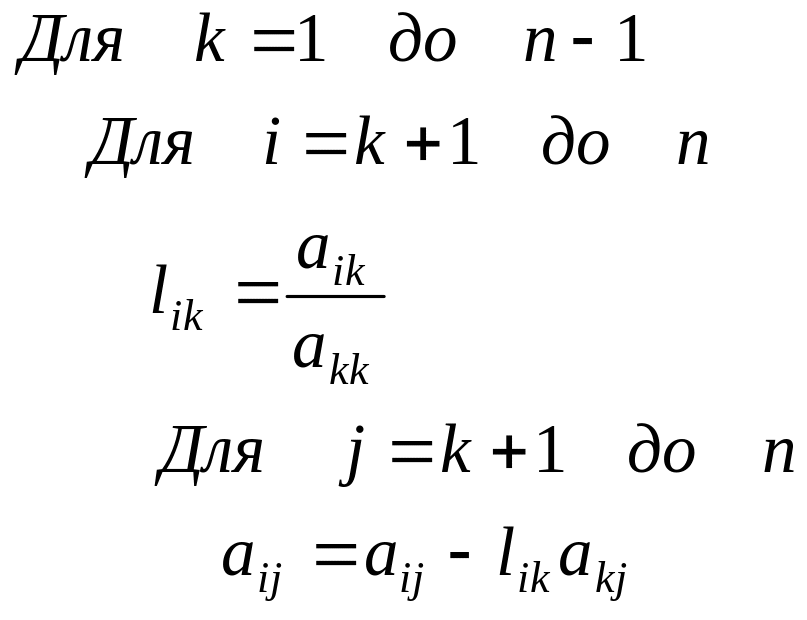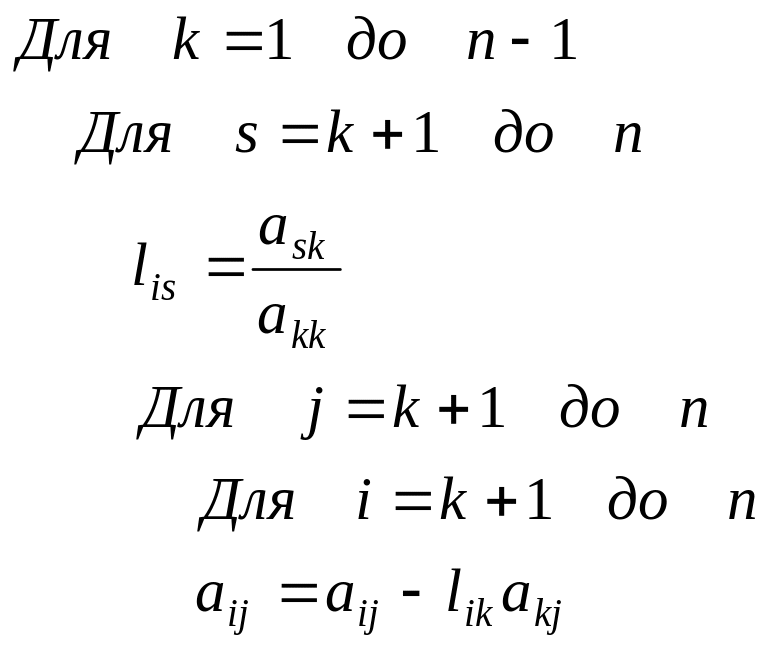- •Содержание
- •1. Численные методы в электротехнических задачах
- •1.1. Численные методы решения систем линейных алгебраических уравнений (слау)
- •1.1.1. Классификация методов
- •1.1.2. Обусловленность системы уравнений
- •1.1.3. Собственные значения и собственные векторы матриц
- •1.1.4. Векторные нормы
- •1.1.5. Методы решения некорректных задач
- •1.1.6. Точные методы расчёта слау
- •1.1.6.1. Классический метод Гаусса
- •I, j, k : IntType;
- •1.1.6.2. Метод Гаусса с выбором главного элемента
- •I,j,k: IntType;
- •I, j, k : IntType;
- •1.1.6.3. Гауссово исключение и lu-разложение
- •1.1.6.4. Матрично-векторные формы - разложения
- •1.1.6.5. Алгоритм Донгарры-Айзенштата.
- •Var I,j,k,s : Integer;
- •Var I,j,k : Integer;
- •1.1.6.6. Метод вращения
- •I, j, k : IntType;
- •I, j, k : IntType;
- •1.1.6.7. Схема Жордана
- •I,j,k : IntType;
- •I, j, k : IntType;
- •1.1.6.8. Факторизация
- •1.1.6.9. Метод квадратных корней (Холесского)
- •I, j, k : IntType;
- •1.1.6.10. Итерационное уточнение
- •1.1.6.11. Особенности решения слау для ленточных симметричных и несимметричных матриц
- •Алгоритм классического метода Гаусса для ленточной симметричной матрицы
- •I, j, k,k1, n , Jend : IntType;
- •I, j, k,k1, n , Jend, c : IntType;
- •1.1.7. Итерационные методы слау
- •1.1.7.1. Решение слау методом простых итераций
- •I, j, k : IntType;
- •X0 : tVector;
- •1.1.7.2. Решение слау методом Гаусса-Зейделя
- •I, j, k : IntType;
- •X0 : tVector;
- •1.1.7.3. Метод релаксации
- •I, j, k : IntType;
- •X0 : tVector;
- •Литература
I,j,k: IntType;
Begin
{Обратный ход}
k:= 0;
S:= A[N,N];
If S<>0.0 Then
For i:=N Downto 1 do
begin
k:= k+1;
S:= B[i];
For j:=i+1 to N do S:= S - A[i,j]*X[j];
X[i]:= S;
{Для Form1.ProgressBar2}
Form1.ProgressBar2.Position:=Round(100*k/N);
end;
End; {Solution}
procedure GaussGlavn(N:IntType;Var A:TMatrix; Var B:TVector; Var X:TVector);
{Метод Гаусса с выбором главного элемента}
Var
I, j, k : IntType;
S : String;
Flag : Boolean;
begin
Form1.Memo1.Visible:= True;
Form1.Memo1.Clear;
FactorizGlavn(N,A,B,X); {Факторизация}
SolutionGlavn(N,A,B,X); {Решение}
For i := 1 to N do
Form1.Memo1.Lines.Add(Format('X[%d] = %f', [i, X[i]]));
For i:= 1 to N do
Form1.StringGrid1.Cells[N+3, i]:= FloatToStrF(1.0*X[i],ffGeneral,3,3);
end;
При реализации данного метода требуется:
выполнить
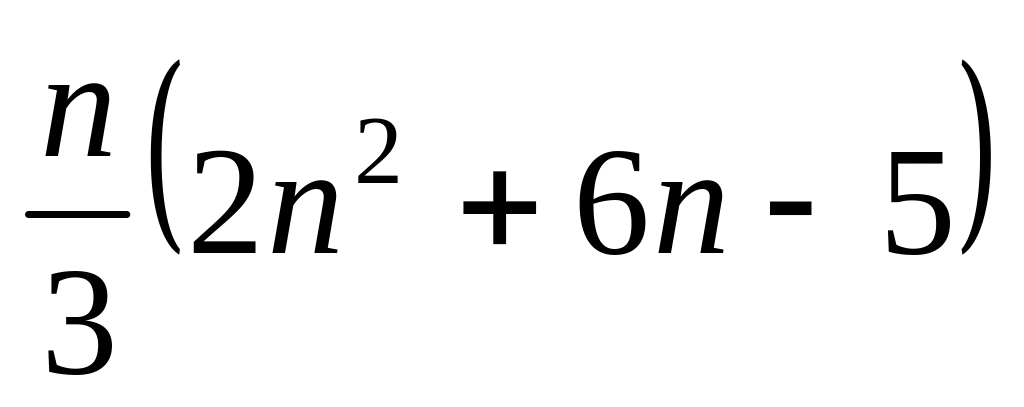 арифметических операций, в том числе
умножений и делений;
арифметических операций, в том числе
умножений и делений;одновременно запоминать
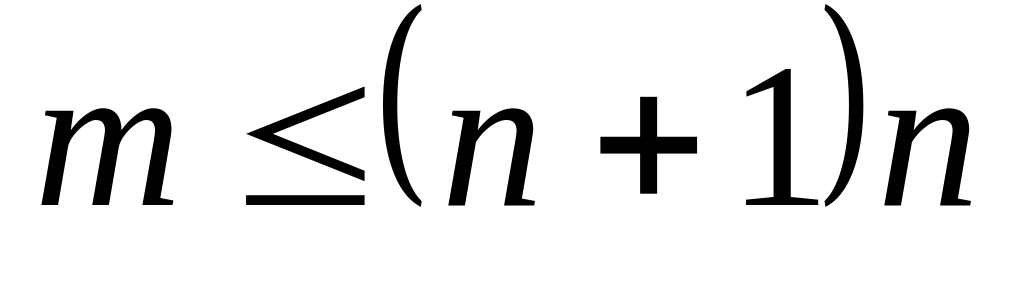 промежуточных результатов.
промежуточных результатов.
Метод главных элементов целесообразно применять в тех случаях, когда:
коэффициенты системы являются дробными числами;
решение должно быть получено с минимальной погрешностью;
порядок системы

 ,
а также когда необходимо решить систему
высокого порядка, у которой матрица
коэффициентов имеет подавляющее
количество нулевых элементов.
,
а также когда необходимо решить систему
высокого порядка, у которой матрица
коэффициентов имеет подавляющее
количество нулевых элементов.
К недостаткам этого метода следует отнести громоздкость вычислительной схемы и сложность программирования.
1.1.6.3. Гауссово исключение и lu-разложение
Пусть необходимо решить систему уравнений
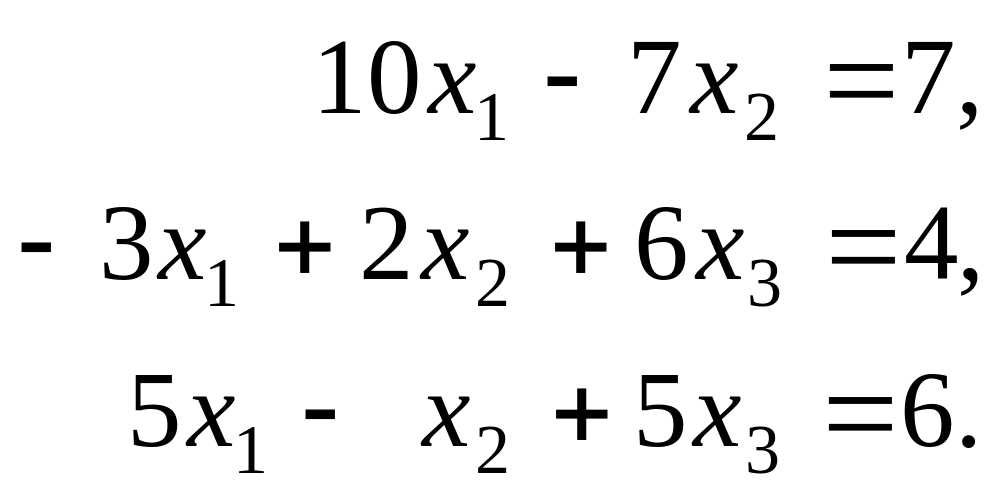
В матричном виде это записывается следующим образом
 .
.
На первом шаге с
помощью первого уравнения
![]() исключается из других уравнений. Это
достигается прибавлением первого
уравнения, умноженного на (0.3) , ко второму
уравнению и прибавлением первого
уравнения, умноженного на (-0.5), к третьему
уравнению:
исключается из других уравнений. Это
достигается прибавлением первого
уравнения, умноженного на (0.3) , ко второму
уравнению и прибавлением первого
уравнения, умноженного на (-0.5), к третьему
уравнению:
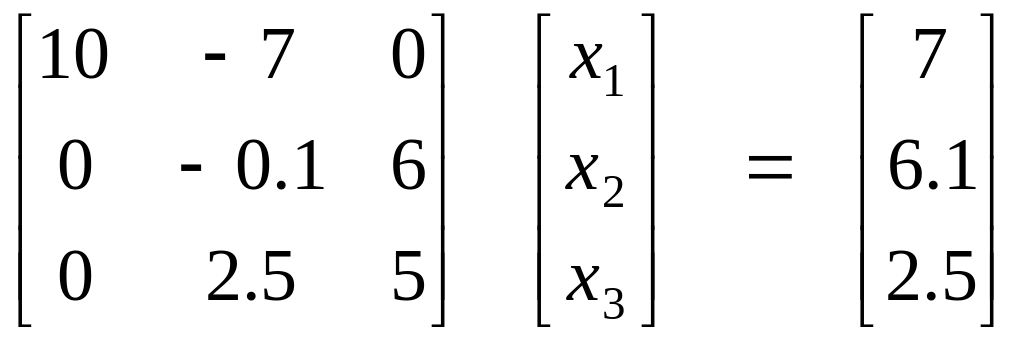 .
.
На втором шаге можно
было бы использовать второе уравнение,
чтобы исключить
![]() из третьего уравнения. Однако коэффициент
при
во втором уравнении – малое число
(-0.1). Поэтому последние два уравнения
переставляются. В данном примере это
делать не обязательно, поскольку здесь
нет ошибок округления, но в общем случае
такие перестановки очень важны. Получаем
из третьего уравнения. Однако коэффициент
при
во втором уравнении – малое число
(-0.1). Поэтому последние два уравнения
переставляются. В данном примере это
делать не обязательно, поскольку здесь
нет ошибок округления, но в общем случае
такие перестановки очень важны. Получаем
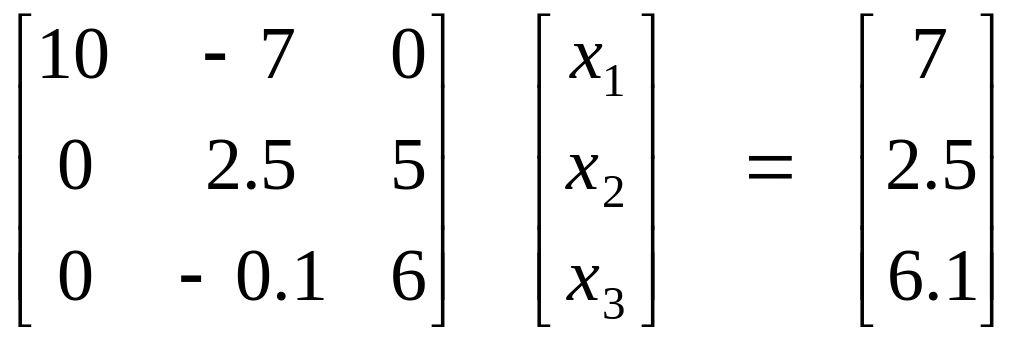 .
.
Теперь с помощью второго уравнения можно исключить из третьего уравнения. Для этого второе уравнение, умноженное на 0.04, прибавляем к третьему уравнению. Получается система
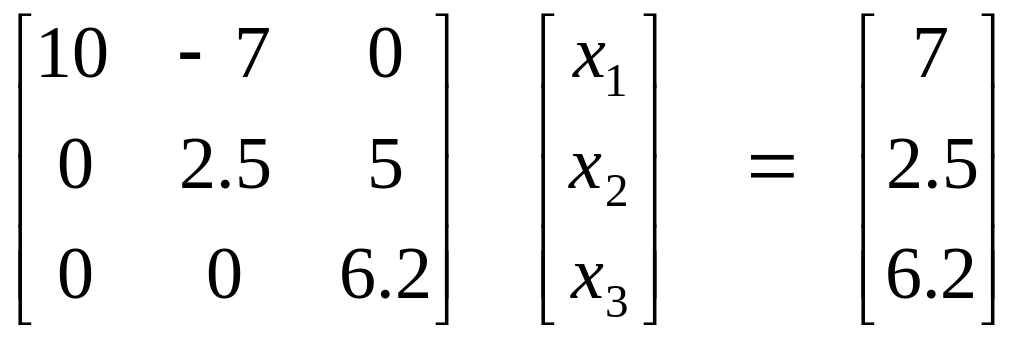 .
.
Получили верхнетреугольную систему, которую решают следующим образом
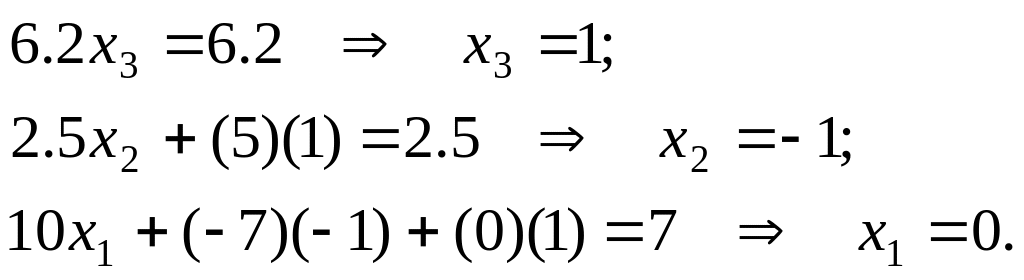
Весь алгоритм можно
записать компактно в матричных
обозначениях. Он соответствует разложению
матрицы
в произведение более простых матриц:
![]() ,
где
,
где
![]() и
- треугольные матрицы, а
- матрица перестановки, хранящая
информацию о переупорядочении строк.
и
- треугольные матрицы, а
- матрица перестановки, хранящая
информацию о переупорядочении строк.
Для разобранного выше примера
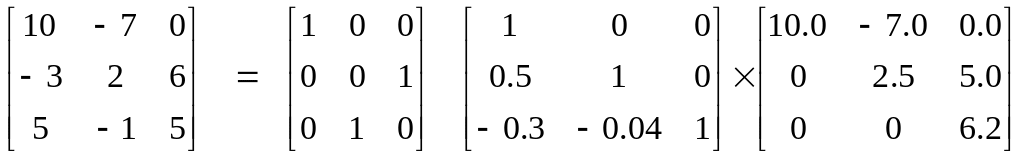 .
.
Матрица - это просто перестановки строк единичной матрицы; она показывает, что при прямом ходе строки 2 и 3 были переставлены. Матрица - это финальная верхнетреугольная матрица, полученная по завершении прямого хода. Множители, использованные в прямом ходе, запоминаются в матрице .
Представление
называется
![]() -разложением
или треугольным
разложением
матрицы
.
Подчеркнём, что никакого нового алгоритма
здесь введено не было. Треугольное
разложение – это гауссово исключение,
выраженное в матричных обозначениях.
-разложением
или треугольным
разложением
матрицы
.
Подчеркнём, что никакого нового алгоритма
здесь введено не было. Треугольное
разложение – это гауссово исключение,
выраженное в матричных обозначениях.
Треугольное разложение
можно сформировать, не зная правую часть
.
После этого решение линейной системы
сводится
к последовательному решению более
простых линейных систем: вначале решается
система
![]() ,
что равносильно переупорядочению
элементов вектора
,
затем система
,
что равносильно переупорядочению
элементов вектора
,
затем система
![]() ,
к которой применяется «прямая подстановка»,
наконец, вектор
определяется
из треугольной системы
,
к которой применяется «прямая подстановка»,
наконец, вектор
определяется
из треугольной системы
![]() ;
здесь используется обратная подстановка.
Математически это можно выразить так:
;
здесь используется обратная подстановка.
Математически это можно выразить так:
![]() ,
,
что эквивалентно решению исходной системы. Применяя эти соображения к разобранному выше примеру, получим:
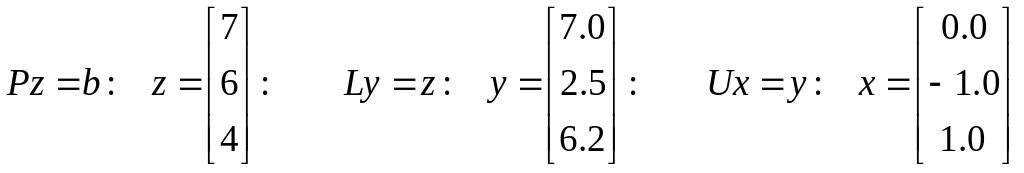
Вычислен тот же, что и раньше, вектор .
Рассмотрим СЛАУ
с
невырожденной матрицей
размера
![]() .
.
Наиболее известной
формой гауссова исключения является
та, в которой система
приводится
к верхнему треугольному виду путём
вычитания одних уравнений, умноженных
на подходящие числа, из других уравнений;
полученная треугольная система решается
с помощью обратной подстановки.
Математически всё это эквивалентно
тому, что вначале строится разложение
![]() ,
где
-
нижняя треугольная матрица с единицами
на главной диагонали, а
-
верхняя треугольная матрица. Затем
решаются треугольные системы
,
где
-
нижняя треугольная матрица с единицами
на главной диагонали, а
-
верхняя треугольная матрица. Затем
решаются треугольные системы
![]() .
.
Процесс их решения называется прямой и обратной подстановками.
Строчно-ориентированная схема - разложения.
Если
хранится по строкам, то полезно
присоединить столбец правых частей к
матрице
,
если это позволяет память, т.е. получить
расширенную матрицу. В таком случае в
цикле
верхняя граница увеличивается до
![]() ,
и длины векторов возрастают на единицу.
,
и длины векторов возрастают на единицу.
Столбцово-ориентированная схема - разложения.
Если
хранится по столбцам, то алгоритм
- разложения
несколько изменится. На
![]() -м
шаге изменённого алгоритма сначала
формируется
-й
столбец матрицы
;
это достигается векторной операцией
деления. В самом внутреннем цикле (цикле
по
-м
шаге изменённого алгоритма сначала
формируется
-й
столбец матрицы
;
это достигается векторной операцией
деления. В самом внутреннем цикле (цикле
по
![]() )
-й
столбец матрицы
)
-й
столбец матрицы
![]() ,умноженный
на число, вычитается из
,умноженный
на число, вычитается из
![]() -го
столбца текущей матрицы
-го
столбца текущей матрицы
![]() ;
длина столбцов равна
;
длина столбцов равна
![]() .
Правая часть
.
Правая часть
![]() может обрабатываться таким же образом,
как столбцы в
;
при этом осуществляется прямая
подстановка.
может обрабатываться таким же образом,
как столбцы в
;
при этом осуществляется прямая
подстановка.
В то же самое время внедрить выбор главного элемента в столбцовую форму более сложно, так как перестановка строк становится проблемой.
Следовательно, если требуется выбор главного элемента и уже хранится по строкам, то строчно-ориентированный алгоритм, вероятно, будет предпочтительным.
-
Строчно-ориентированная схема
 -
разложения
-
разложенияСтолбцово-ориентированная схема - разложения