I, j, k : IntType;
C,S : RealType;
AK : Matrix;
BK : Vector;
Begin
{Прямой ход исключения переменных}
For k:= 1 to N-1 do
For i:= k+1 to N do
begin
C:= A[k,k]/(Sqrt(Sqr(A[k,k])+Sqr(A[i,k])));
S:= A[i,k]/(Sqrt(Sqr(A[k,k])+Sqr(A[i,k])));
For j:=1 to N do
begin
AK[k,j]:=C*A[k,j]+S*A[i,j];
A[i,j]:= - S*A[k,j] + C*A[i,j];
AK[k,j]:= A[k,j];
end;
BK[k]:= C*B[k] + S*B[i];
B[i]:= -S*B[k] + C*B[i];
BK[k]:= B[k];
B[i]:= B[i];
end;
end;
Procedure GivensSol(N:IntType; Var A:Matrix; Var B,X:Vector);
{Обратный ход: последовательное нахождение корней }
{Гивенс. Решение.}
Var
I, j, k : IntType;
h : RealType;
Begin
For i:= 1 to N do
For j:= 1 to i-1 do
B[i]:= B[i] - A[i,j]*B[j];
X[N]:= B[N]/A[N,N];
For i:= N-1 downto 1 do
begin
h:= B[i];
For j:= i+1 to N do h:= h - X[j] * A[i,j];
X[i]:= h/A[i,i];
end;
end;
GivensFac(N,A,B);
GivensSol(N,A,B,X);
1.1.6.7. Схема Жордана
Модификацией метода главных элементов является метод диагональных элементов, называемый также схемой Жордана.
Сущность его состоит в том, исходная матрица приводится к диагональному виду, после чего по диагональным элементам легко находятся неизвестные.
На каждом этапе исключения неизвестных число уравнений не уменьшается, но при выборе главного элемента учитывается только те уравнения, из которых главный элемент ещё не выбирался.
Используем расширенную матрицу, т.е. к матрице коэффициентов добавляется столбец правой части.
Вычисления ведутся по формулам
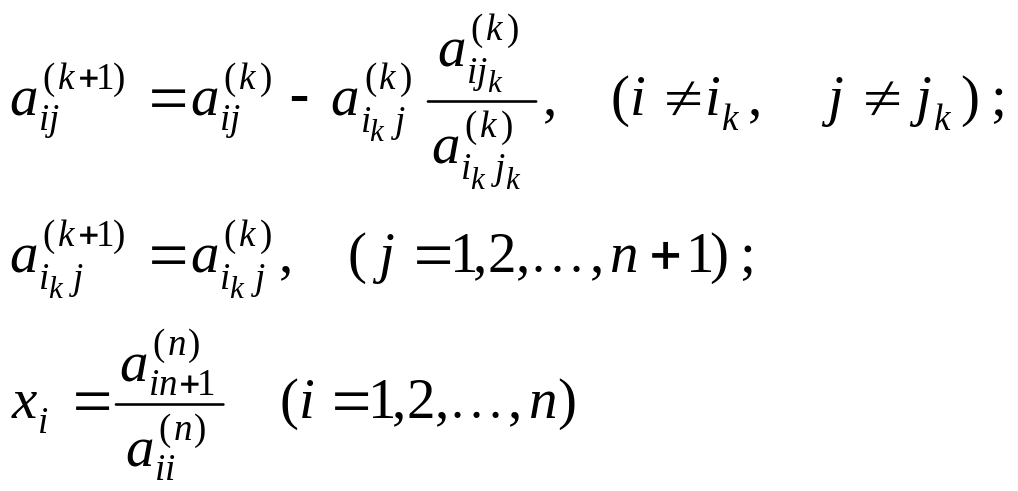
Перед использованием
последней формулы необходимо, чтобы
стоки матрицы
были упорядочены, т. е. приведены к
диагональному виду
Алгоритм:
Выбор главного элемента
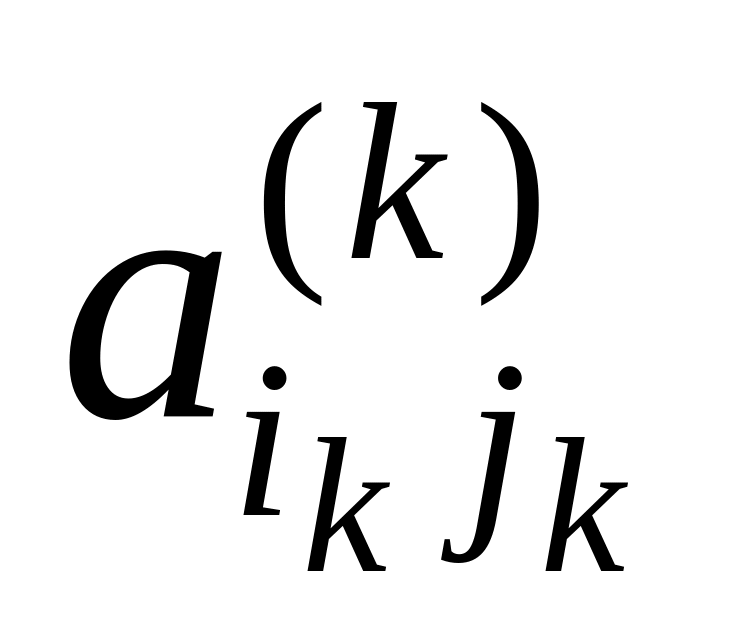матрицы
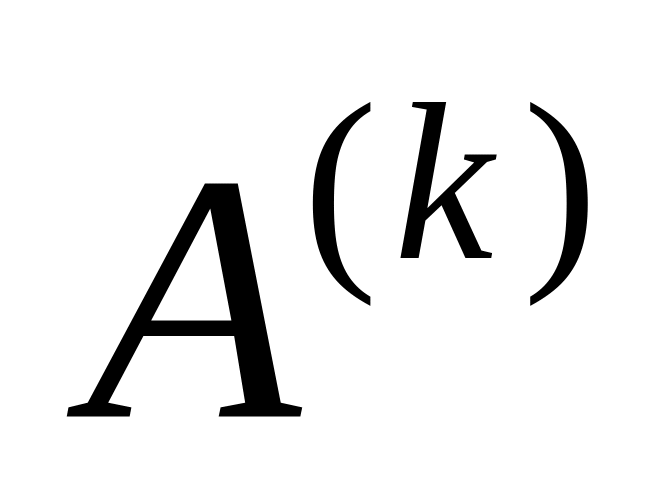при фиксированном значении
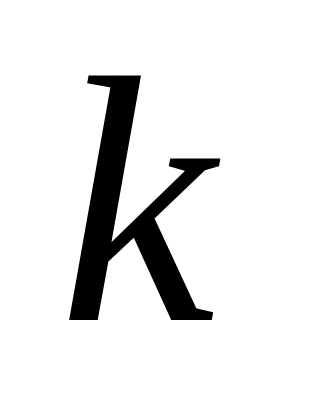(начиная
с
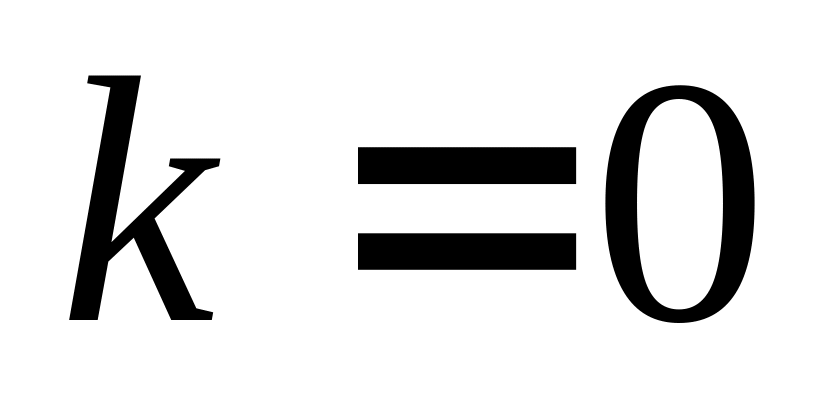).Исключение
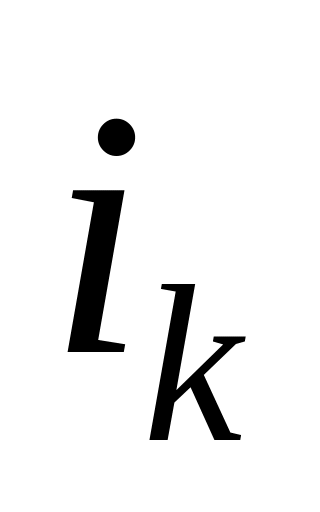-й
строки из дальнейшего рассмотрения
при выборе главного элемента.Определение элементов матрицы
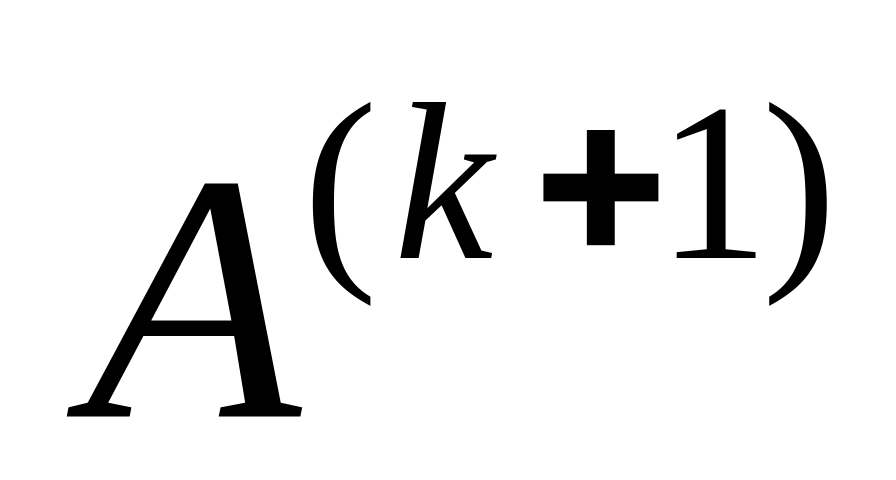по первой формуле.Определение элементов -й строки той же матрицы из второго равенства.
Проверка выполнения условия
.
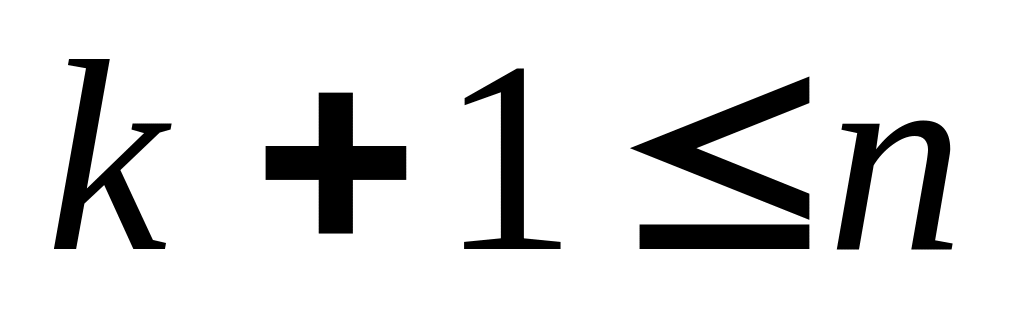При (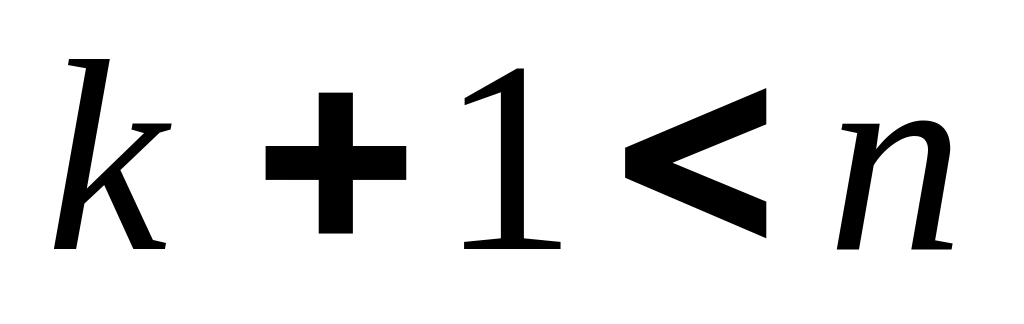
)
увеличивается
на единицу
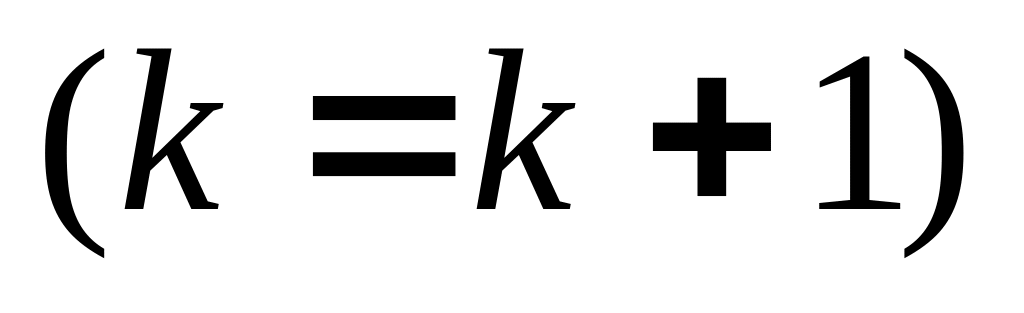и управление передаётся п. 1, в случае
равенства
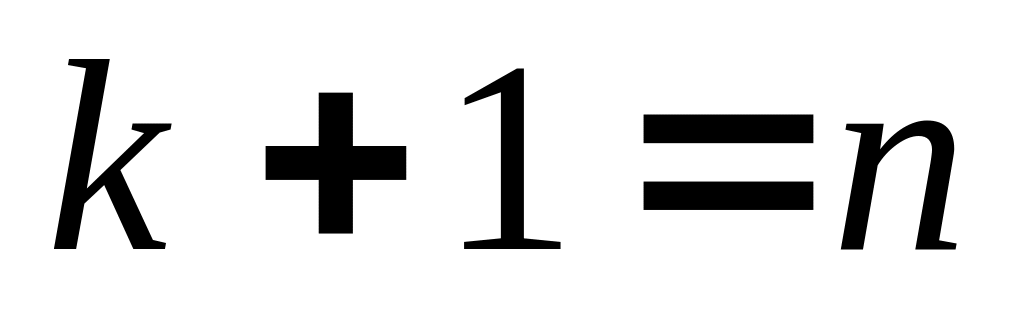выполняется п. 6.Приведение матрицы к диагональному виду путём перестановки строк.
Определение неизвестных
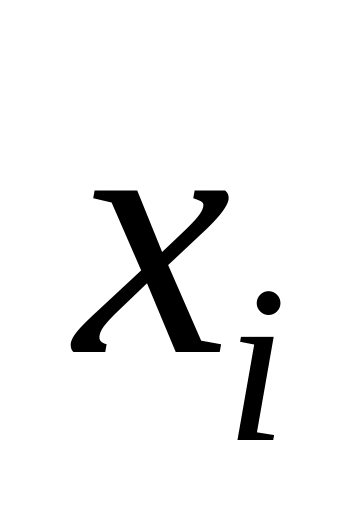по последней формуле.
Данный метод рекомендуется применять при решении плохо обусловленных систем невысокого порядка, а также в случаях, когда другие методы не дают достаточной точности.
Пример 1.9.
Procedure FactorizJordan(N:IntType; Var A:TMatrix; Var B:TVector);
//Процедура факторизации
Var
k,i,j : IntType;
R,S : RealType;
q : TVector;
SS : String;
Begin
{прямой ход}
For k:= 1 to N do
For i:=1{для м. Гаусса с i:= k+1} to N do
If i<>k Then
begin
q[i]:= -A[i,k]/A[k,k];
For j:= 1 to N do
If j=k Then A[i,j]:=0
else
A[i,j]:= A[i,j]+ q[i]*A[k,j];
B[i]:=B[i]+q[i]*B[k];
end
else Continue;
{Вывод диагональной матрицы (к методу Жордана)}
Form1.Memo1.Lines.Add(' Вывод диагональной матрицы A(к методу Жордана)');
For i := 1 to N do
begin
SS := '';
For j := 1 to N do
begin
SS := SS+ Format('%f'#9, [A[i,j]]);
end;
SS := SS+ Format('%f'#9, [B[i]]);
Form1.Memo1.Lines.Add(SS);
end;
End; {Factoriz}
Procedure SolutionJordan(N:IntType; Var A:TMatrix; Var B:TVector;Var X:TVector);
//Процедура нахождения решения
Var
S : RealType;