Аппроксимационная теорема Вейерштрасса.

Любую непрерывную функцию можно приблизить на замкнутом интервале некоторым полиномом .

Если - произвольная непрерывная на конечном замкнутом интервале функция, то для любого найдётся такой полином степени , что

.

Если выбрать в качестве базисных функций неотрицательные целые степени переменной

,

то модель примет вид

с матрицей

Определить матрицы можно вычислить по формуле

,

который не равен нулю, если все различны.

3.2.2. Вычисление значений многочлена. Схема Горнера

Полиномы столь распространены в математике, что часто приходится сталкиваться с проблемой быстрого их вычисления по заданным коэффициентам. Полином

можно вычислить по схеме Горнера:

.

3.2.3. Линейная интерполяция

Единственный линейный интерполянт для точек и задаётся формулой

,

где и удовлетворяют уравнениям

и , т. е. .

Если , то матрица невырожденная и можно найти и ,

решая систему в матричном виде или развернутом .

Тогда получим

.

3.2.4. Квадратичная интерполяция

Найдём квадратический интерполянт по точкам .

Таким интерполянтом является

.

Все находятся из условия, что полином должен проходить через три указанные точки; это приводит к системе уравнений

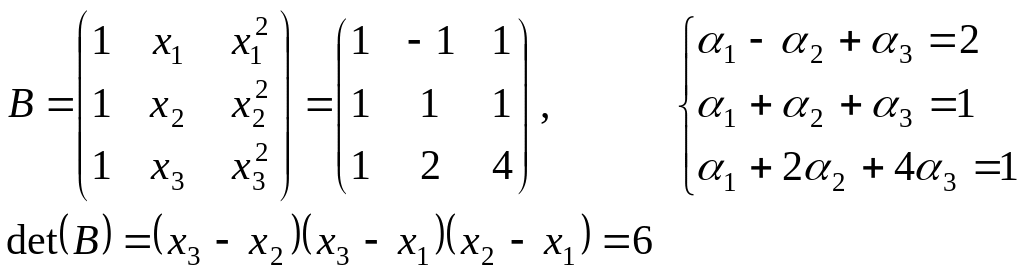
Подставив в матричное уравнение значения, получим

.

Решение этой системы даст интерполянт

.

Вывод: для заданных на плоскости точек с различными абсциссами существует единственный полином степени не выше , который проходит через все эти точки.

3.2.5. Построение других базисных функций

Если в линейном интерполянте в качестве базисных функций выбрать

Тогда получится матрица

,

т. е. единичная матрица и где

Решением системы уравнений будут и . Поскольку существует только один многочлен первой степени, проходящий через две различные точки, а это значит, что можно записать

;

одно выражение есть просто алгебраическое преобразование другого.

Другие изменения, которые мы можем сделать, это переставить и так, что , или заменить и на сумму и разность: и . Любая замена функций на другой набор независимых функций, которые являются линейными комбинациями исходных, не влияет на получающийся интерполянт и называется заменой представления или заменой базиса.

Замена базиса может быть полезной, если она приводит к более простому выражению или даёт дополнительное представление о задаче.

3.2.6. Многочлены Тейлора

Многочленом Тейлора степени функции в точке называется многочлен

.

Многочлен Тейлора обладает тем свойством, что в точке все его производные порядка включительно совпадают с соответствующими производными функции , т. е.

.

Погрешность, возникающая при замене функции её многочленом Тейлора, выражается остаточным членом формулы Тейлора:

,

где , - некоторая точка, лежащая строго между и при .

3.2.7. Лагранжева интерполяция

Определим ниже базис Лагранжа (Жозеф Луи Лагранж (1736-1813), уроженец Турина) получается заменой базиса, которая приводит к точно такому же интерполянту, однако для нового базиса матрица будет единичной.

Предположим, что у нас есть набор функций , каждая из которых является полиномом степени , а также удовлетворяет условию

Иными словами, принимает значение 1 в точке и равна нулю во всех других точках . (Отметим, и , указанные в начале этого раздела, обладают таким свойством.) Любая линейная комбинация функций снова является полиномом степени . Рассмотрим в частности,

.

Из свойств следует, что

.

Поэтому является интерполяционным полиномом, а поскольку такой полином единственный, это эквивалентно решению линейной системы. При этом

.

Лагранжева интерполяция по трём заданным точкам

.

В виду сложности вычисления коэффициентов их можно вычислять раздельно для полиномов с при ординатах.

При нормировке

,

где разность абсцисс соседних узлов,

.

Вычисление коэффициентов полинома Лагранжа при трёх ординатах :

.

Вычисление коэффициентов полинома Лагранжа при четырёх ординатах и :

.

Вычисление коэффициентов полинома Лагранжа при пяти ординатах и :

.

Вычисление коэффициентов полинома Лагранжа при шести ординатах и :

.

Пример.

program PLagrang;

{вычисление полинома Лагранжа в n+1 узле интерполяции}

Uses Crt;

Const

M=15;

Type

RealType = Real;

Vec=Array[0..M] of RealType;

Var