5. Теория алгоритмов и конечные автоматы

5.1. Алгоритмы Вопросы для повторения

1. Дайте интуитивное определение алгоритма.

2. Перечислите основные варианты математического определения алгоритма.

5.1. Алгоритм вычисления числа , основанный на формуле удвоения.

Решение

Исторически первый и в течение длительного времени единствен­ный алгоритм вычисления числа  был основан на подсчете периметров правильных вписанных и описанных многоугольников с помощью фор­мул удвоения. Эта формула связывает длины сторон правильных n- и 2n-угольников, вписанных в окружность радиуса R. Положим диаметр рассматриваемой окружности равным единице: d = 2R = 1 (длина такой окружности равна n), тогда формула удвоения примет вид:

.

Умножим и разделим выражение под знаком общего корня на сопряжен­ное. В результате получим:

.

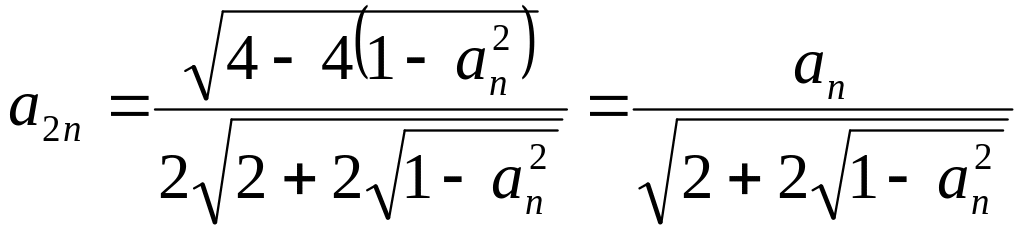Введем периметр многоугольника и подставим выражения сто­рон и через периметры в формулу, тогда она преобразуется к виду

.

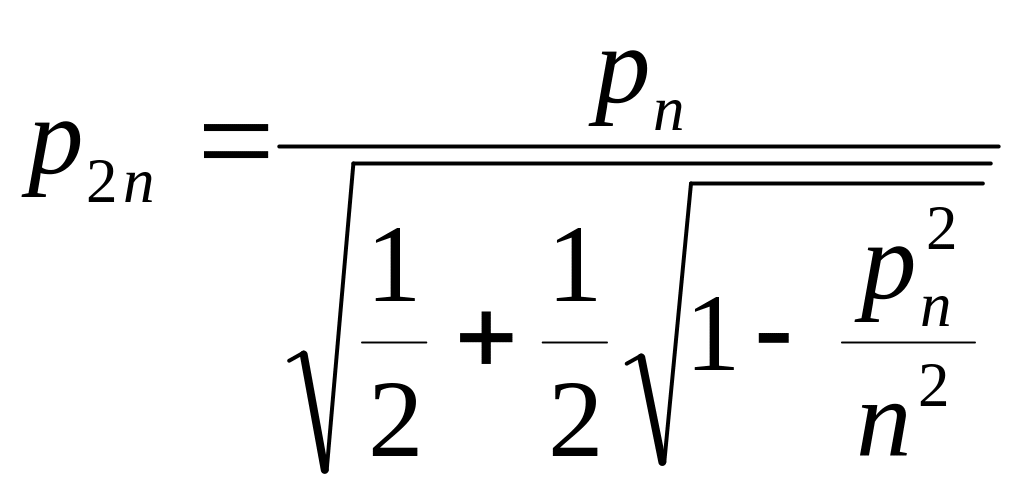Мы получили рекуррентную формулу.

Сторона правильного описанного n-угольника при d = 2R = 1 выра­жается через сторону вписанного n-угольника с помощью соотношения

.

Перейдем в нем от сторон и к соответствующим периметрам, обозначая периметр вписанного многоугольника через : . В ре­зультате будем иметь:

.

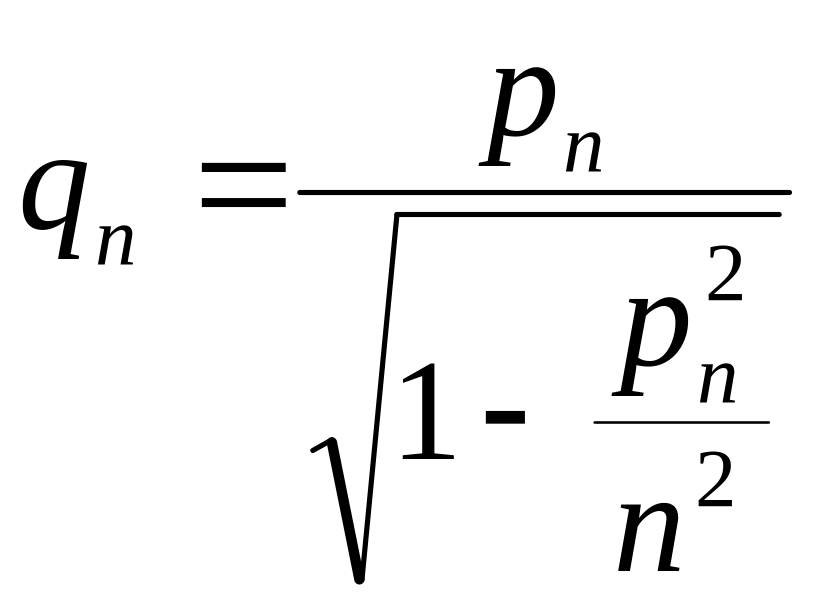Но .

Вычисление числа  с помощью данного метода можно начать с какого-нибудь простого правильного многоугольника, например с ше­стиугольника, для которого

, .

Далее процесс строится следующим образом: по рекуррентной форму­ле находятся последовательно . По ним с помощью формулы вычисляются соответствующие значения .

Двухстороннее неравенство позволяет утверждать, что найденные на некотором шаге числа дают приближенные значения  с недостатком и избытком с ошибкой , которая стремится к нулю при .

Используя описанные идеи и проводя сложнейшие для своего време­ни вычисления, древнегреческий ученый Архимед дошел до правильного 96-угольника и получил для двухстороннюю оценку:

, .

В Европе французский математик Ф. Виет нашел 9 правильных цифр числа  после запятой с помощью -угольника (16 удвоений числа сторон).

Приведем таблицу 16 удвоений числа сторон (табл. 5.1): повторение результата Ф. Виета.

Таблица 5.1

Таблица 16 удвоений числа сторон для вычисления числа 

k
0	6	3,000 000 000 000	3,464 101 615 138
1	12	3,105 828 541 230	3,630 002 002 236
2	24	3,132 628 613 281	3,245 155 564 194
3	48	3,139 350 203 047	3,166 557 423 678
4	96	3,141 031 950 890	3,147 778 817 495
5	192	3,141 452 472 285	3,143 135 797 312
6	384	3,141 557 607 912	3,141 978 227 840
7	768	3,141 583 892 148	3,141 689 033 932
8	1536	3,141 590 463 228	3,141 616 747 849
9	3072	3,141 592 105 999	3,141 598 677 103
10	6144	3,141 592 516 692	3,141 594 159 465
11	12288	3,141 592 619 365	3,141 593 030 059
12	24576	3,141 592 645 034	3,141 592 747 706
13	49152	3,141 592 651 034	3,141 592 677 119
14	98304	3,141 592 653 055	3,141 592 659 472
15	196608	3,141 592 653 456	3,141 592 655 060
16	393216	3,141 592 653 556	3,141 592 653 957

Для оценки точности определения  с помощью этих расчетов со­ставим разность периметров и , приведенных в последней строке :

.

Первые 10 знаков у чисел и совпадают, т. е.  = 3,141 592 653....