34

Раздел I. Линейная алгебра

Практическое занятие №1

Матрицы. Действия над матрицами

Рассмотрим прямоугольную таблицу чисел:

.

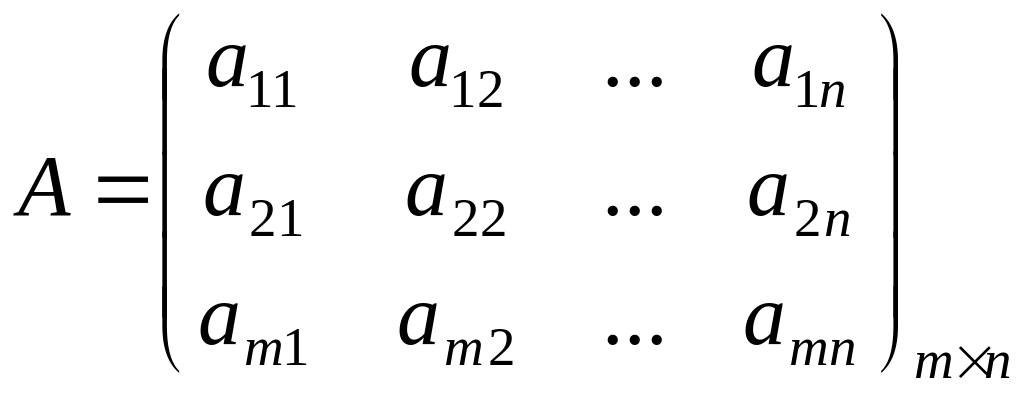Данная таблица чисел называется матрицей размерности , где m – количество строк; n – количество столбцов.

Числа называются элементами данной матрицы А. Индексы i и j указывают номера строки и столбца, в пересечении которых стоит элемент ( 3-я строка, 2-й столбец). Если , то матрица А называется квадратной порядка n. Элементы образуют главную диагональ матрицы А. Квадратная матрица, у которой на главной диагонали стоят единицы, а все остальные элементы – нулевые, называется единичной матрицей.

Единичная матрица любого порядка обозначается Е.

Например,

это единичная матрица второго порядка.

это единичная матрица третьего порядка.

Суммой матриц одинаковой размерности называется матрица той же размерности, каждый элемент которой равен сумме соответствующих элементов матриц А и В: .

Произведением матрицы на число называется матрица , получающаяся из матрицы А умножением всех ее элементов на число k:

.

Пример 1. а) Выполнить сложение двух матриц:

.

.

.

Произведением матрицы размерности на матрицу размерности называется матрица размерности , каждый элемент которой , стоящий в i-й строке и k-м столбце, равен сумме парных произведений соответствующих элементов i-й строки матрицы А и k-го столбца матрицы В:

.

Пример 2. Перемножить матрицы:

Эти матрицы можно перемножить, т.к. количество столбцов первой матрицы равно количеству строк второй матрицы . Получилась матрица размерности 33, т.е. квадратная матрица порядка 3.

Выполнить задания:

1. Даны матрицы . Проверить, выполняется ли равенство .

2. Вычислить , если

а) ;

б) .

3. Выполнить действия над матрицами:

а) ;

б) ;

в) ;

г) .

4. Найти , если .

Практическое занятие №2

Определители второго и третьего порядков. Свойства определителей.

Определители произвольного порядка

Определителем второго порядка, соответствующем квадратной матрице называется число, равное:

(1)

Например, .

Определителем третьего порядка, соответствующим квадратной матрице называется число

(2)

При вычислении определителя третьего порядка полезно использовать схему Саррюса:

Например,

.

Определители произвольного порядка

Минором элемента определителя третьего порядка называется определитель второго порядка, который получится, если в исходном определителе вычеркнуть строку и столбец, содержащие данный элемент .

Алгебраическим дополнением элемента называется число, которое вычисляется по формуле:

Знаки перед минорами для алгебраических дополнений элементов определителя третьего порядка определяются таблицей:

.

Таблица знаков для алгебраических дополнений элементов определителя четвертого порядка:

.

Пример 1. Вычислить миноры и и алгебраические дополнения и для определителя:

Решение.

и т.д.

и т.д.

Используя определение алгебраических дополнений и формулу (см. формулу определителя третьего порядка), можно записать определитель третьего порядка следующей формулой:

(3)

В формуле (3) определитель представлен разложением по элементам первой строки. По аналогичной формуле можно ввести понятие определителя четвертого порядка:

(4)

Свойства определителей

Сформулируем основные свойства определителей, присущие определителям всех порядков.

Свойство 1. Определитель не изменится, если его строки заменить столбцами, и наоборот. Т.е. , где матрица, транспонированная матрице А.

Свойство 2. Общий множитель элементов какой-либо строки (столбца) можно выносить за знак определителя.

Свойство 3. При перестановке двух строк (столбцов) определитель меняет знак на противоположный.

Проверим это свойство на примере определителя второго порядка:

.

Свойство 4. Если какие-либо две строки (столбца) определителя пропорциональны, то определитель равен нулю.

Свойство 5. Если в определителе элементы двух строк (столбцов) соответственно равны друг другу, то определитель равен нулю.

Свойство 6. Если определитель имеет столбец (строку) из нулей, то определитель равен нулю.

Свойство 7. Определитель треугольной матрицы равен произведению элементов, стоящих на главной диагонали.

Свойство 8. Определитель не изменится, если к элементам одной строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.

Пример 2. Вычислить определитель разложением по элементам второго столбца:

Пример 3. Вычислить определитель, используя свойства:

Выполнить задания:

1. Объяснить равенства:

а) ;

б) ;

в) ;

г) .

2. Вычислить определитель, приведя его к треугольному виду:

а)

б) .

3. Вычислить определитель разложением по элементам сначала первой строки, а затем по элементам второго столбца:

а) ; б) ;

в) ; г) ;

д) ; е) .