7. Принцип максимуму модуля для голоморфних функцій.

Теорема 1. Якщо функція є голоморфною в області , то її модуль не може приймати в найбільше значення.

Доведення. Припустимо протилежне, тобто що існує точка така, що . В деякому околі точки функція розвивається в ряд Тейлора

.

Звідси випливає, що для кожного функція розвивається в ряд Фур’є

.

На підставі рівності Парсеваля

.

Але

.

Тому

.

Отже, для всіх , тобто . Суперечність. ►

Наслідок 1. Якщо функція є голоморфною в обмеженій області і неперервною на , то

.

Доведення. Справді, згідно з теоремою Вейєрштрасса неперервна функція приймає в найбільше значення, яке мусить прийматися на на підставі принципу максимуму. ►

Наслідок 2. Якщо функція є голоморфною в крузі , то і функція є зростаючою на .

Доведення. Цей наслідок випливає безпосередньо з теореми 1. ►

Наслідок 3. Якщо функція є голоморфною в області і не має нулів в , то її модуль не може приймати в найменше значення.

Доведення. Для отримання цього наслідку досить застосувати теорему 1 до функції . ►

Приклад 1. Нехай – довільна точка круга . Покажемо, що для всіх виконується . Справді, нехай , . Тоді для всіх маємо

Тому на підставі наслідку 1 приходимо до потрібного висновку.

Приклад 2. , якщо . Справді, це випливає з рівностей

Приклад 3. Для всіх , всіх і кожної голоморфної в крузі , , функції виконується .

Справді, оскільки для кожного виконується

,

то

,

звідки випливає потрібне.

Приклад 4. Для всіх , всіх і кожної голоморфної в крузі , , функції виконується .

Справді, це випливає з рівності .

Приклад 5. і , якщо і .

Справді, . Якщо , то . Але

,

, , , .

Тому для всіх . Робимо висновок, що

, .

8. Ряд Лорана. Ряд

(1)

називається узагальненим степеневим рядом. Ряд (1) називається збіжним, якщо збіжним є кожний із рядів

, .

Перший з цих рядів є степеневим рядом і він збігається в крузі , де , а другий зводиться до степеневого заміною . Він збігається для тих z, для яких , де

.

Отож, узагальнений степеневий ряд (1) є збіжним в кільці . Якщо це кільце не є порожнім, то на кожному компакті з нього збіжність є рівномірною, а його сума є голоморфною функцією в ньому.

Теорема 1. Якщо узагальнений степеневий ряд (1) збігається в кільці , , то його сума (функція ) є голоморфною функцією в і коефіцієнти знаходяться за формулою

, (2)

і останній інтеграл від не залежить, де – сума ряду (1).

Доведення. Згідно з теоремою Абеля, ряд (1) рівномірно збігається на кожному компакті із кільця . Тому функція є голоморфною в . Отож, інтеграл (1) від не залежить. Для кожного маємо

і на останній ряд збіжний рівномірно. Тому, враховуючи що

отримуємо

,

звідки випливає (2). ►

Узагальнений степеневий ряд (1), коефіцієнти якого визначені за формулою (2), називається рядом Лорана в кільці голоморфної в цьому кільці функції , а також рядом Лорана функції в околі точки , якщо .

Теорема 2 (Лорана). Кожну голоморфну в кільці , , , функцію можна розвинути в цьому кільці в ряд Лорана

.

Доведення. Нехай – довільна точка. Візьмемо числа і так, щоб На підставі інтегральної формули Коші

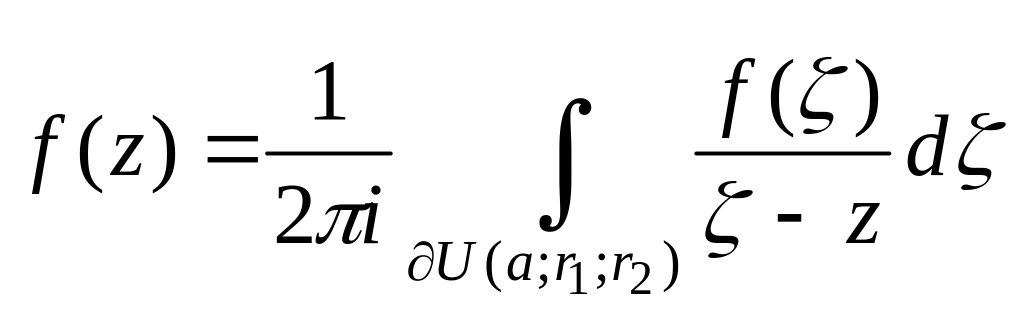
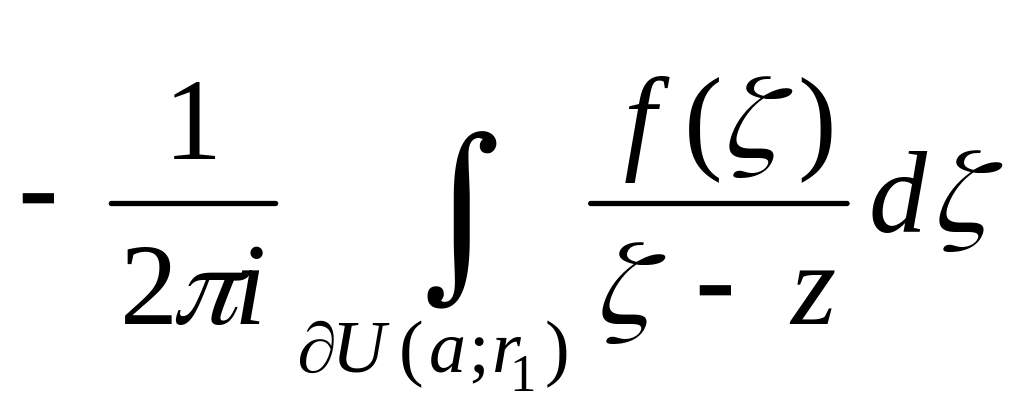. (3)

Але

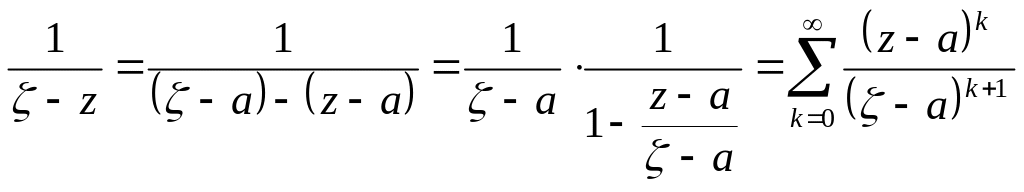
Р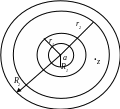 ис. 1

і для вибраного z останній ряд на збігається рівномірно, бо . Тому

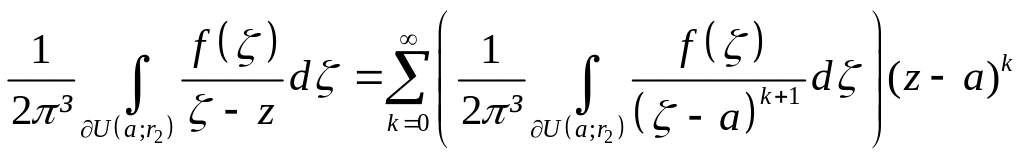= . (4)

Окрім цього,

,

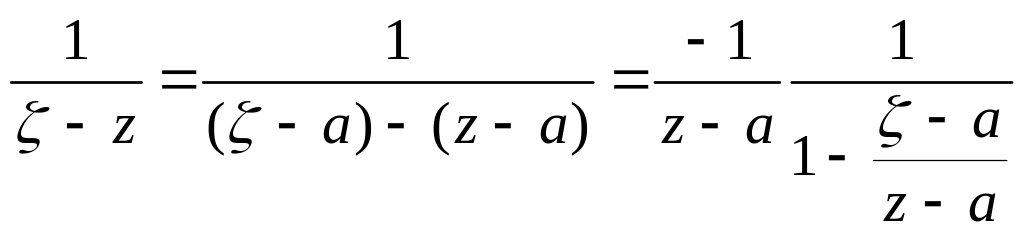
і для вибраного z на останній ряд збігається рівномірно, бо . Тому

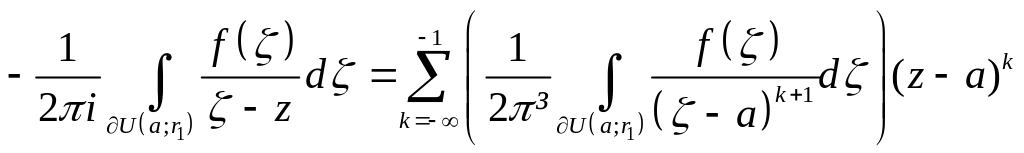
Звідси та з (3) і (4) випливає твердження теореми 2. ►

Ряди

,

називають відповідно головною і голоморфною (правильною) частиною ряду Лорана функції в околі точки .

Теорема 3. Кожну функцію , голоморфну в кільці , , можна розвинути в цьому кільці в ряд Лорана

(5)

і при цьому

. (6)

Теорема 4. Кожну функцію , голоморфну в кільці , можна розвинути в цьому кільці в ряд Лорана

(7)

і при цьому

. (8)

Доведення. Ці дві теореми є частковим випадком теореми 1. ►

Рядом Лорана функції в околі називається ряд (7), коефіцієнти якого визначені за формулою (8). При цьому ряди

,

називаються відповідно головною і голоморфною (правильною) частиною ряду Лорана в околі .

Наслідок 1. Для будь-яких , та , , система утворює базу простору .

Приклад 1. Ряд є збіжним у кільці і є розбіжним поза замиканням цього кільця.

Справді, ряд є степеневим і він є збіжним, якщо , бо, позначивши , отримуємо, що

, ,

.

Дослідження ряду зводиться до дослідження степеневого ряду, бо

.

Якщо , то

, ,

і тому останній ряд є збіжним, якщо .

Приклад 2. Розвинемо в ряд Лорана в околі точки функцію . Маємо

,

і останній ряд збігається в крузі .

Приклад 3. Розвинемо в ряд Лорана в околі точки функцію . Маємо

,

і останній ряд збігається в кільці .

Приклад 4. Розвинемо в ряд Лорана в околі точки функцію

.

Маємо

,

і останній ряд збігається в кільці , тобто в .

Приклад 5. Розвинемо в ряд Лорана за степенями функцію

.

Ця задача має декілька розв’язків, оскільки не вказано в якому кільці слід розвинути. Маємо

,

це розвинення справедливе в крузі і отриманий ряд Лорана співпадає з рядом Тейлора розглядуваної функції в цьому крузі. Далі,

і останній ряд збігається в кільці . Крім цього,

і останнє розвинення справедливо в кільці . Отож, ми отримали три ряди Лорана даної функції за степенями у відповідних кільцях, одне з яких вироджується в круг. Формально можна аналогічно отримати ще один ряд

Проте ряд

збігається в крузі , а ряд

в кільці і . Тому отримане розвинення не є справедливим в жодному кільці.

9. Особливі точки голоморфних функцій. Особливою точкою функції , голоморфної в області , називається кожна точка . Особлива називається ізольованою особливою точкою функції , голоморфної в області , якщо є голоморфною в деякім проколенім околі точки , тобто, якщо деякий проколений окіл точки належить . Особлива точка функції , голоморфної в області , називається її усувною особливою точкою, якщо існують область і голоморфна в функція такі, що і . Усувна особлива точка не є, фактично, особливою точкою. Її можна усунути, приписавши певне значення функції в цій точці. Отож, якщо – ізольована особлива точка функції , то є голоморфною в деякім проколенім околі точки і розвивається в цьому околі в ряд Лорана

, ,

,

Зокрема, точка  є ізольованою особливою точкою функції , якщо можна вказати таке значення , що в області функція не має особливих точок, що знаходяться на скінченній відстані від точки .

Приклад 1. Функція є голоморфною в області . Тому точка є її особливою точкою. Функція

є голоморфною в області і для . Тому точка є усувною ізольованою особливою точкою.

Приклад 2. Точки , є ізольованими особливими точками функції , а точка не є ізольованою особливою точкою цієї функції.

Приклад 3. Ряд

(1)

є збіжним в крузі і функція є голоморфною в цьому крузі. Сума цього ряду для дорівнює . Функція є голоморфною в області . Точка є її ізольованою неусувною особливою точкою. Правда, можна було б розглядати функцію (1) як функцію з в . Тоді можна сказати, що кожна точка є її особливою точкою. Всі точки , окрім , є усувними неізольованими особливими точками функції , а точка є неусувною особливою точкою. Цей приклад показує, що при розгляді особливих точок потрібно звертати увагу на область, в якій дана функція розглядається. На це вказує і наступний приклад.

Приклад 4. Функція

, ,

є голоморфною в області , функція

, ,

є голоморфною в області і не є голоморфною в жодній іншій області , яка містить . Функція

, ,

є голоморфною в області і не є голоморфною в жодній іншій області , яка містить . Крім цього, для і , . Кожна точка є особливою точкою функції . Всі точки , крім , є усувними. Точка є неусувною особливою точкою цієї функції. Всі точки , є неусувними особливими точками функції . Всі точки , є неусувними особливими точками функції .

Зауваження 1. Для кожної області існує голоморфна в цій області функція , яка не є голоморфною в жодній іншій області (доведення дивись в [18]).

Зауваження 2. Приклад 4 показує, що для заданої функції , голоморфної в області не можна, взагалі кажучи, говорити про максимальну область , в яку можна продовжити як голоморфну функцію, оскільки таких областей може існувати декілька. Наприклад, для функції , розглянутої в прикладі 4, такими областями є, зокрема, області , , а також кожна інша область, яка отримується з шляхом викидання довільного променя з початком в точці . Водночас, для багатьох функцій максимальна область голоморфності існує і тоді така функція, якщо не вказано на інше, розглядається в цій максимальній області. Так часто буває, коли функція задана деякою формулою, яка містить тільки однозначні функції.

Зауваження 3. Розглянуті вище приклади вказують на те, що є певні труднощі з означенням особливих точок голоморфних функцій. У наведеному вище означенні роль області є істотною. Кожна функція , голоморфна в області , є гілкою в деякої повної аналітичної функції і наведене вище означення особливої точки функції, голоморфної в , трохи відрізняється від означення особливої точки повної аналітичної функції, про що говоритиметься далі.

10. Критерій ізольованої усувної точки. Точка а∂D називається ізольованою точкою межі області D, якщо деякий її проколений окіл належить D. Наприклад, точка ізольована точка межі області .

Теорема 1. Нехай точка є ізольованою точкою межі області D, а функція є голоморфною в області D. Тоді наступні умови є еквівалентними: 1) точка є усувною особливою точкою функції ; 2) існує скінченна границя ; 3) розвинення функції в ряд Лорана в околі точки не містить головної частини, тобто ряд Лорана є і рядом Тейлора.

Доведення (за діаграмою (1231)). Нехай виконується 1). Тоді існує функція , яка є голоморфною в точці і в деякому проколеному околі точки . Тому . Звідси випливає 2). Нехай виконується 2) і для конкретності припустимо, що . Нехай

(1)

– коефіцієнти ряду Лорана функції в околі точки . Оскільки виконується 2), то . Тому з (1) отримуємо, що . Спрямувавши до , отримуємо, що для всіх , тобто 3) виконується. Якщо виконується 3), то сума ряду Лорана функції в околі точки є голоморфною функцією в цьому околі і тому 1) виконується. ►

Приклад 1. Переконаємось, що точка є усувною ізольованою особливою точкою функції . Справді, ця функція є голоморфною в області , точка є ізольованою точкою межі області і

.

Точка  є усувною особливою точкою функції , якщо розвинення в ряд Лорана функції не містить членів з додатними степенями , тобто

.

11. Критерій полюса. Полюсом функції , голоморфної в області D, називається така її ізольована особлива точка , для якої

. (1)

Теорема 1. Для того щоб точка була полюсом функції , необхідно і достатньо, щоб ця точка була нулем функції .

Доведення. Ця теорема випливає безпосередньо з означень. ►

Порядком полюса функції називається порядок нуля функції . Якщо , то полюс називається простим.

Теорема 2. Нехай точка є ізольованою точкою межі області D, а функція є голоморфною в D. Тоді наступні умови є еквівалентними: 1) точка є полюсом порядку ; 2) подається у вигляді , де – функція, голоморфна в точці , причому ; 3) лоранове розвинення функції в околі точки має вигляд

, , (2)

Доведення. Ця теорема випливає безпосередньо із означень та відповідної теореми для нулів. ►

Наступне твердження є аналогом теореми 3 для .

Теорема 3. Нехай точка є ізольованою точкою межі області D, а функція є голоморфною в D. Тоді наступні умови є еквівалентними: 1) точка є полюсом порядку ; 2) подається у вигляді де  – голоморфна в , причому ; 3) ряд Лорана функції в околі має вигляд

, .

Нагадаємо, що функція називається голоморфною в точці , якщо функція є голоморфною в точці .

Приклад 1. Точка є полюсом четвертого порядку функції . Справді, функція в точці має простий нуль. Отже, подається у вигляді , де є голоморфною функцією в точці і . Тому і функція є голоморфною в точці і . Отож, і справді розглядувана функція має в точці полюс четвертого порядку.

Приклад 2. Точка є полюсом третього порядку функції . Розвинемо дану функцію в ряд Лорана в околі . Маємо

.

і на підставі теореми 3 приходимо до потрібного висновку.

12. Критерій суттєво особливої точки. Суттєво особливою або суттєво особливою точкою функції , голоморфної в області D, називається така її ізольована особлива точка , для якої не існує в .

Теорема 1. Нехай – ізольована точка межі області D і функція є голоморфною в D. Для того щоб точка була суттєво особливою точкою функції , необхідно і достатньо, щоб головна частина її ряду Лорана в околі точки містила нескінченну кількість членів, відмінних від нуля.

Доведення. Справді, з попередніх теорем випливає, що суттєво особлива точка не може бути ні усувною, ні полюсом функції . У цих двох випадках, і тільки в них, головна частина ряду Лорана містить скінченне число членів. Звідси випливає потрібне. ►

Теорема 2 (Сохоцького-Вейєрштрасса). Якщо – суттєво особлива точка функції , голоморфної в області D, то для будь-якого існує послідовність така, що , i .

Доведення. Нехай спочатку . Функція не може бути обмеженою в жодному проколеному околі точки . Тому в для кожного існує таке, що і, таким чином, так побудована послідовність є шуканою. Нехай тепер . Якщо для кожного рівняння має розв’язок , то послідовність є шуканою. Якщо рівняння не має розв’язків в деякому проколеному околі точки , то точка є суттєво особливою точкою функції . Отже, за доведеним вище існує послідовність , збіжна до , така, що . Звідси випливає, що , що і доводить потрібне. ►

Приклад 1. Переконаємось, що точка є суттєво особливою точкою функції . Розвинемо дану функцію в ряд Лорана в околі . Маємо

і на підставі теореми 1 приходимо до потрібного висновку.

Приклад 2. Знайдемо всі особливі точки функції . Скінченними особливими точками даної функції є і . Запишемо функцію у вигляді

.

Але

.

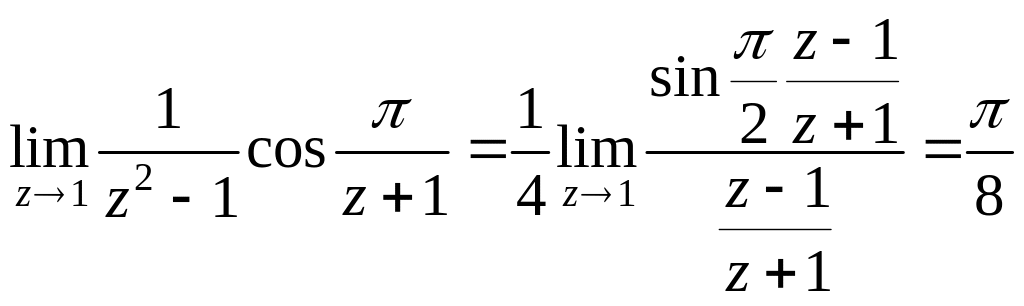Тому є усувною особливою точкою. Щоб визначити характер точки , розвинемо функцію в ряд Лорана

.

Звідси випливає, що у головній частині ряду Лорана є нескінченно багато членів, а отже точка є істотно особливою точкою для функції . Оскільки , то точка є істотно особливою точкою для функції f. Далі

,

тобто точка є усувною особливою точкою.

Приклад 3. Знайдемо всі особливі точки функції та з’ясуємо їх характер. Особливими точками є тільки точки і . Розвинемо функцію в ряд Лорана в кільці

.

Якщо цей ряд розглядати як ряд Лорана в околі точки , то в його головній частині нема членів, і тому є усувною особливою точкою. А якщо його розглядати як ряд Лорана в околі точки , то в його головній частині є нескінченно багато членів, і тому є істотно особливою точкою.

13. Особливі точки на межі круга збіжності степеневого ряду.

Теорема 1. Якщо степеневий ряд

(1)

має радіус збіжності , то голоморфна в функція f має принаймні одну неусувну особливу точку .

Д оведення. Припустимо, що всі точки є усувними. Тоді для точки існують круг і голоморфна в функція такі, що

Рис. 1

для кожного виконується . Круги покривають . Оскільки є компактом, то існує скінченне підпокриття , причому перетин для всіх не є порожнім, де і . Звідси та з теореми єдиності випливає, що для . Тому існує така (однозначна) голоморфна в крузі , , функція F, що , якщо . Функція F розвивається в в степеневий ряд, причому . Тому ряд (1) має радіус збіжності . Суперечність. ►

Наслідок 1. Якщо функція є голоморфною в області D, кожна точка межі області D є її неусувною особливою точкою і , то радіус збіжності ряду Тейлора

дорівнює відстані від точки до множини неусувних особливих точок функції .

Приклад 1. – радіус збіжності ряду Тейлора в околі точки функції .

Справді, ця функція є голоморфною в області , кожна точка є її неусувною особливою точкою. Тому .

Зауваження 1. Для функції , голоморфної в області , і точки маємо розвинення

,

і – радіус збіжності останнього ряду. Точка – єдина скінченна особлива точка функції , . Водночас, відстань від точки до дорівнює . Це вказує на істотність в наслідку 1 вимоги, щоб кожна точка була неусувною особливою точкою.

Приклад 2. Існують такі степеневі ряди, для яких кожна точка круга збіжності є неусувною особливою точкою його суми. Прикладом може служити ряд

.

Справді, ця функція є голоморфною в крузі і при , бо при всіх i

.

Але . Тому при . Аналогічно, і тому

, .

Але в будь-якому околі кожної точки є нескінченно багато точок виду , , . Тому кожна точка є неусувною особливою точкою функції .

Якщо функція є голоморфною в області D і не існують область D₁ і голоморфна в D₁ функція такі, що , i при , то кажуть, що є природною межею функції . Можна довести, що межа кожної області є природною межею деякої голоморфної в цій області функції .