18

Содержание

3.1 Постановка задачи численного интегрирования. 2

3.2 Основные методы построения квадратурных формул 3

Задачи для самостоятельного решения 8

3.3 Оценка погрешности квадратурных формул 9

3.4 Метод Ричардсона практической оценки точности квадратурных формул 12

Задачи для самостоятельного решения 14

Задания к лабораторной работе 15

Контрольные вопросы к лабораторной работе 17

Литература 18

Лабораторная работа №3

Численное интегрирование

3.1 Постановка задачи численного интегрирования.

Основные понятия

Пусть вычисляется интеграл , причем функция такова, что неопределенный интеграл от неё или не вычисляется в элементарных функциях или функция задана в виде таблицы. Вместо слов, численное вычисление определённых интегралов, часто используют термин вычисление квадратур, дабы избежать путаницы с численным интегрированием обыкновенных дифференциальных уравнений и по этой причине формулы приближенного вычисления интегралов называют квадратурными формулами.

Пусть [a, b] конечный интервал оси х разбит на n интервалов, которые называются элементарными отрезками или подинтервалами [ . Положим , а через обозначим длину i-го элементарного отрезка, тогда

, (1)

который можно представить в виде , разбивая промежуток интегрирования, где интеграл по подинтервалу.

Аналитическую формулу, дающую приближённое значение называют простой (элементарной) квадратурной формулой, а формулу, дающую значение , называют составной квадратурной формулой.

Итак, задача численного интегрирования состоит в вычислении приближённого значения интеграла (1) ,т.е. в построении составной квадратурной формулы, проведении численного расчета и оценке погрешности вычислений.

3.2 Основные методы построения квадратурных формул.

Наиболее распространённые методы построения квадратурных формул основаны на использовании аппарата интерполирования, либо получаются, на основе интерполяционных формул, методом неопределённых коэффициентов.

Рассмотрим простейший пример построения элементарных квадратур методом неопределённых коэффициентов. Без ограничения общности можем рассматривать элементарный отрезок [-h, h] и количество узлов в нём выбирать, исходя из точности квадратуры.

Приведём рассмотрение случаев одного, двух и трёх узлов на отрезке [-h, h] при построении квадратурных формул, которые будут точны, соответственно, на полиномах нулевой, первой и второй степеней¹.

а) Квадратурная формула, точная для многочленов нулевой степени (формула прямоугольников).

Эта квадратура может быть получена из интерполяционного полинома построенного по одному узлу. Т.е. элементарная квадратура имеет вид следующего равенства:

,

с неопределенным коэффициентом .Погрешность этой квадратуры равная

, (2)

должна обращаться в нуль на многочленах нулевой степени, т.е. при мы должны иметь , т.к. является линейным функционалом. Для получаем уравнение из равенства (2)

,

т.е. имеем простую квадратуру

,

которую легко обобщить для i-го элементарного интервала, по следующей схеме: соответствует нижнему пределу интегрирования i-го элементарного интервала , , соответствует средина промежутка интегрирования

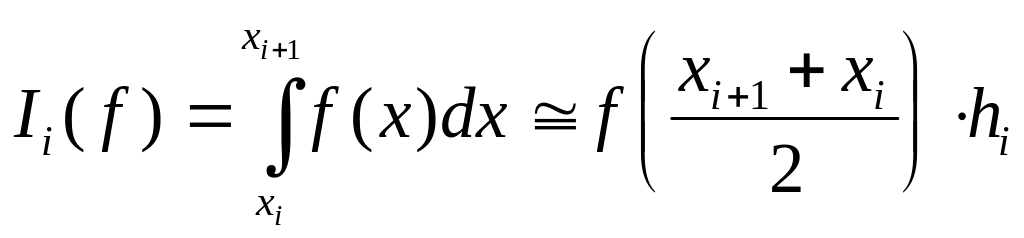. (2а)

Легко установить геометрический смысл этой квадратуры, (из которого становится очевидным название квадратуры- как формулы прямоугольников). Из приведенного ниже рисунка, где наклонными линиями заштрихована фигура, площадь которой равна а вертикальными линиями заштрихован прямоугольник с площадью даваемой квадратурной формулой (2а)

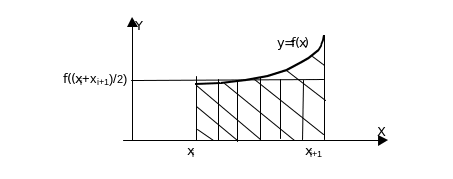
Рис.1

б) Квадратурная формула, точная для многочленов первой степени (формула трапеций).

В этом случае мы должны строить квадратуру по двум узлам -h, h.

.

Неопределённые коэффициенты и мы определим из условия обращения в нуль и

Таким образом, имеем простую квадратуру

,

которая легко обобщается для любого i-го элементарного подинтервала

. (2б)

Геометрический смысл этой формулы (дающей ей название формулы трапеций) легко установить из приведённого ниже рисунка, где наклонными линиями заштрихована фигура, площадь которой равна , а вертикальными линиями заштрихована трапеция с площадью даваемой квадратурной формулой (2б)

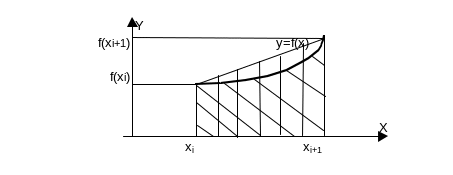
Рис.2

в) Квадратурная формула, точная для многочленов второй степени (формула Симпсона или формула парабол).

В этом случае мы должны строить квадратуру уже по трем узлам -h, 0, h

.

Из условия обращения в ноль получаем систему трёх уравнений на коэффициенты

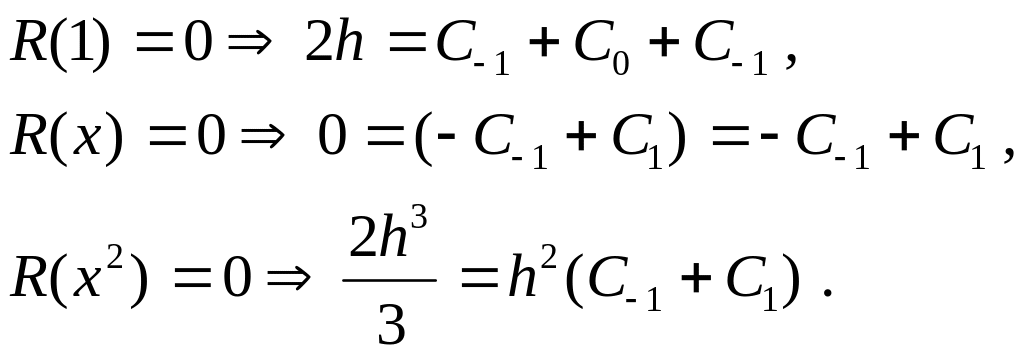
Решая эту систему, получаем

.

Таким образом, элементарная квадратура имеет вид

,

ее обобщение для i-го элементарного подинтервала имеет вид

.

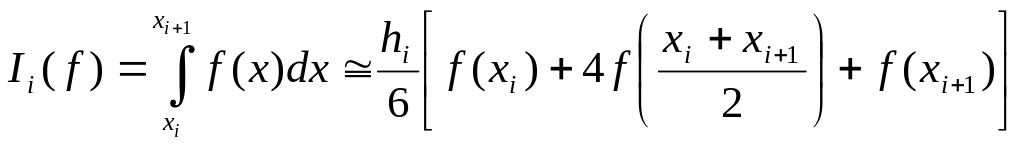Аналогично предыдущему можно провести геометрическую интерпретацию формулы Симпсона (2в). Предлагается выполнить это задание самостоятельно. Окончательно выпишем элементарные квадратуры для всех рассмотренных случаев:

а) формула прямоугольников ;

б) формула трапеций ;

в) формула Симпсона .

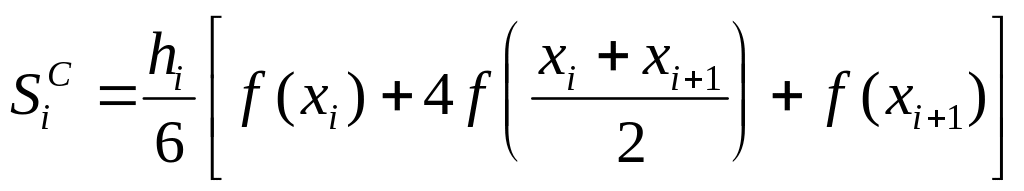Мы установили, что эти квадратурные формулы являются точными соответственно для полиномов 0-й, 1-й и 2-й степеней, но нет никаких ограничений, которые бы запрещали этим формулам быть точными для полиномов более высоких степеней, что мы и увидим позже, когда займёмся оценкой погрешностей квадратурных формул.

Задачи для самостоятельного решения.

1. Построить квадратурные формулы исходя из аппарата интерполирования.

2. Построить квадратуры прямоугольников и трапеций, непосредственно вычисляя площади фигур, получаемых в результате разбиения.

3. Типичной задачей прикладной математики является отыскание решения интегрального уравнения

,

где и заданы, а задача состоит в вычислении .

Если мы приблизим интеграл посредством квадратурной формулы

,

то интегральное уравнение превратится в систему линейных алгебраических уравнений. Ее решение , , есть искомое дискретное приближение к функции .

Используя формулу Симпсона, постройте приближенную систему для интегрального уравнения

.

Сравните полученное решение с точным в различных точках интервала .

4. Найдите веса формулы Ньютона-Котеса 8-го порядка, потребовав, чтобы приближенное равенство

было точным для , .