
- •Название контрольной работы по мс:
- •1 Основные понятия и теоремы
- •2 Примеры задач с решениями
- •2.1 Задачи на основные понятия и теоремы теории вероятностей
- •2.2 Задачи на использование комбинаторики при подсчёте вероятностей
- •2.3 Задачи на формулу полной вероятности и формулу Байеса
- •2.4 Вычисление вероятности наступления события в серии n независимых испытаний
- •2.5 Нахождение законов распределения случайных величин, их числовых характеристик, функций и плотностей распределения
- •2.6 Нахождение законов распределения двумерных случайных величин
- •3 Список рекомендуемых источников
- •Приложение а. Варианты заданий для контрольной работы
- •Приложение б. Справочные таблицы
Название контрольной работы по мс:
Определение параметров линейной регрессии с помощью метода наименьших квадратов. Прогнозирование одного фактора на основе другого.
1 Основные понятия и теоремы
Теория вероятностей – математическая наука, изучающая закономерности случайных явлений.
Случайное явление – явление, которое при неоднократном воспроизведении одного и того же опыта (при неоднократных испытаниях) протекает каждый раз несколько по-иному.
Опыт (испытание) – всякое осуществление определённого комплекса условий или действий, при которых происходит соответствующее явление.
Событие - возможный результат опыта.
Случайное событие – событие, которое при осуществлении данного опыта может наступить, а может и не наступить.
Достоверное событие (U) – событие, которое при осуществлении данного опыта всегда наступит.
Невозможное событие (V) – событие, которое при осуществлении данного опыта никогда наступит.
Равновозможные события – события, для которых при осуществлении данного опыта нет оснований считать, что возможность появления одного из них больше, чем другого.
Несовместные события – события, которые при осуществлении данного опыта не могут наступить одновременно (появление одного из них исключает появление других в одном и том же опыте).
Полная группа событий (совокупность единственно возможных событий) – группа таких событий, для которых выполняется: в результате данного опыта обязательно происходит и только одно из них.
Противоположные
события – события А и
![]() ,
для которых выполняется: в результате
данного опыта наступление А
равносильно тому, что
не наступит.
,
для которых выполняется: в результате
данного опыта наступление А
равносильно тому, что
не наступит.
Элементарные исходы (случаи, шансы) – равновозможные, несовместные события, образующие полную группу событий.
Пространство
элементарных исходов – совокупность
элементарных исходов
![]() .
Часто используют обозначение:
.
Часто используют обозначение:
![]() .
Любой результат эксперимента (событие)
- это точка пространства
.
Любой результат эксперимента (событие)
- это точка пространства
![]() .
Если можно считать, что ни один из
элементарных исходов (случаев) не
является предпочтительным, т.е. исходы
равновозможны, каждому элементарному
исходу можно приписать число
.
Если можно считать, что ни один из
элементарных исходов (случаев) не
является предпочтительным, т.е. исходы
равновозможны, каждому элементарному
исходу можно приписать число
![]() .
Это число называют вероятностью данного
случая. Таким образом, для нахождения
вероятности необходимо найти число
элементарных исходов.
.
Это число называют вероятностью данного
случая. Таким образом, для нахождения
вероятности необходимо найти число
элементарных исходов.
Благоприятные (благоприятствующие) случаи (для события) – случаи, при которых данное событие наступает. Появление благоприятного случая является проявлением данного события.
Классическое определение вероятности
Пусть m – число элементарных исходов, благоприятствующих событию А, n – число всех равновозможных элементарных исходов опыта, в котором может появиться это событие. Вероятностью события А называется отношение m/n:
Р(А) = m/n. (1)
Свойства вероятности
для достоверного события U выполняется: Р(U) = 1;
для невозможного события V: Р(V) = 0;
для случайного события A: 0 < P(A) < 1;
для любого события В: 0 ≤ Р(В) ≤ 1.
Комбинаторика – раздел математики, изучающий количества комбинаций, подчиняющихся определённым условиям, которые можно составить из элементов заданного конечного множества.
Правило суммы
Если некоторый объект А может быть выбран из совокупности объектов m способами, а В – другими k способами, то выбрать объект А+В (А или В) можно m+k способами.
Правило произведения
Если объект А может быть выбран из совокупности объектов m способами, а после каждого такого выбора объект В может быть выбран k способами, то выбор упорядоченной пары АВ (А∙В, А и В) может быть произведён m∙k способами.
Размещения
– комбинации,
составленные из n
различных элементов по m
элементов (m
≤ n),
которые отличаются либо составом
элементов, либо их порядком. Число всех
возможных размещений
![]() :
:
![]() . (2)
. (2)
Перестановки
– комбинации, составленные из n
различных элементов по n
элементов,
отличающихся только порядком их
расположения. Число всех возможных
перестановок
![]() :
:
![]() . (3)
. (3)
Сочетания
– комбинации, составленные из данных
n
различных элементов по m
элементов (m
≤ n),
которые отличаются хотя бы одним
элементом. Число сочетаний
![]() :
:
![]() . (2)
. (2)
Перестановки с повторениями – комбинации, составленные из данных n элементов, среди которых n1 элементов одного вида, n2 элементов другого вида и т.д.: n1 + n2 + …+ nk = n. Число перестановок с повторениями можно подсчитать по формуле:
![]() . (5)
. (5)
Размещения с повторениями – комбинации, составленные из n различных элементов по m элементов (элементы в таких комбинациях могут повторяться, при этом может оказаться, что n ≤ m). Число размещений с повторениями находят по формуле:
![]() . (6)
. (6)
Сочетания с повторениями – комбинации, составленных из n различных элементов по m элементов, элементы в которых могут повторяться, но в отличие от числа размещений с повторениями, последовательность при выборе элементов не важна. Число таких комбинаций находят по формуле:
![]() . (7)
. (7)
Геометрическая
вероятность
– обобщение классической вероятностной
модели с конечным или счётным числом
равновероятных элементарных исходов.
Пусть пространству элементарных исходов
соответствует некоторый выделенный
объём
![]() (площадь
(площадь
![]() или длина
или длина
![]() );
а событию А
соответствует некоторая область с
объёмом
);
а событию А
соответствует некоторая область с
объёмом
![]() (площадью
(площадью
![]() или длиной
или длиной
![]() ).
Тогда вероятностью события А
можно считать отношение:
).
Тогда вероятностью события А
можно считать отношение:
![]() . (3)
. (3)
Статистическая
вероятность
– число, близкое к m/n
при неограниченном возрастании n
– числа независимых испытаний, если m
– число появлений события А
в этой серии из n
испытаний. Величина m/n
называется относительной
частотой
события А
(или частостью).
При этом справедлива теорема Бернулли
(частный случай теоремы Чебышева - одного
из законов больших чисел [1, с. 97]). Согласно
этой теореме, в описанной ситуации для
любого положительного числа
![]() предел вероятности события
предел вероятности события
![]() равен 1:
равен 1:
![]() .
.
Предел, используемый в теореме Чебышева, называют пределом по вероятности. Таким образом, практически достоверным при больших значениях n является событие: вероятность р события А сколь угодно близка к его относительной частоте m/n.
Сумма или объединение событий – событие, состоящее в появлении хотя бы одного из них.
Произведение (пересечение) событий – событие, состоящее в одновременном появлении этих событий.
Сумму трёх событий (А1, А2, А3) можно рассмотреть как сумму события (А1+А2) и события А3; аналогично для четырёх, пяти событий и так далее (так же и произведение нескольких событий).
Обобщая понятия, связанные с действиями над событиями, на множестве событий вводят алгебраические операции (используя символику действий над множествами):
объединение (сумма) двух событий А и В – событие С, такое, что
 ;
;дополнение (противоположное событию А) – событие
 ,
такое, что
,
такое, что
 ;
;пересечение (произведение) двух событий А и В – событие С, такое, что
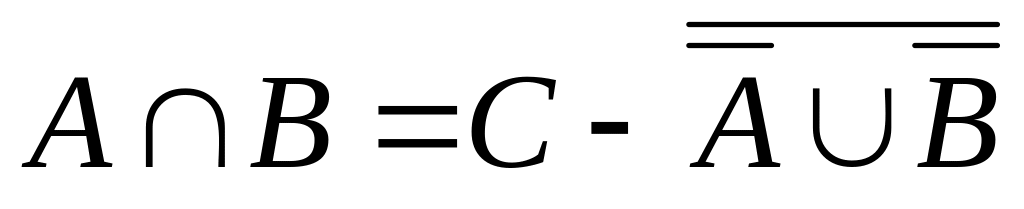 ;
; следствие (из А следует В, А включается в В, А влечёт В):
 ;
;невозможное событие
 ;
;достоверное событие
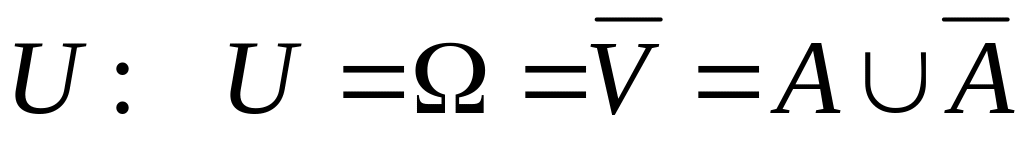 ;
;разность двух событий А и В – событие С, такое, что
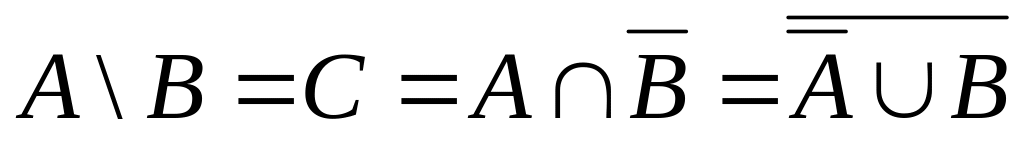 ;
;симметрическая разность двух событий А и В – событие С, такое, что
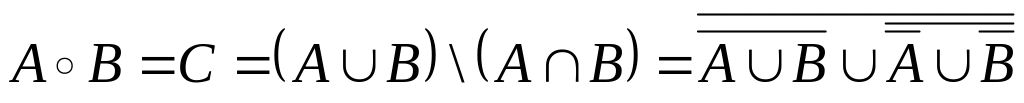
Алгебра событий
Множество событий S называется алгеброй событий, если выполняются следующие условия (аксиомы событий):
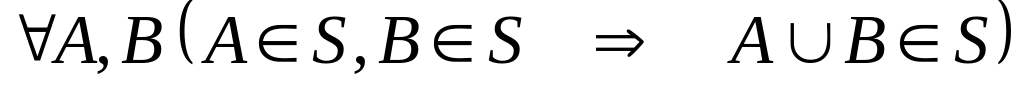 ;
;
Припишем каждому
элементарному событию (исходу)
![]() некоторый «вес»
некоторый «вес»
![]() – вероятность
исхода
– вероятность
исхода
![]() .
Совокупность вероятностей должна
удовлетворять условиям:
.
Совокупность вероятностей должна
удовлетворять условиям:
 ,
, .
.
В этом случае
вероятность некоторого события А
определяется
формулой:
![]() .
При этом тройка
.
При этом тройка
![]() ,
где
,
где
![]() ,
а S
– некоторая алгебра подмножеств
[2, с. 54], определяет вероятностную модель,
или вероятностное пространство,
обладающее свойствами:
,
а S
– некоторая алгебра подмножеств
[2, с. 54], определяет вероятностную модель,
или вероятностное пространство,
обладающее свойствами:
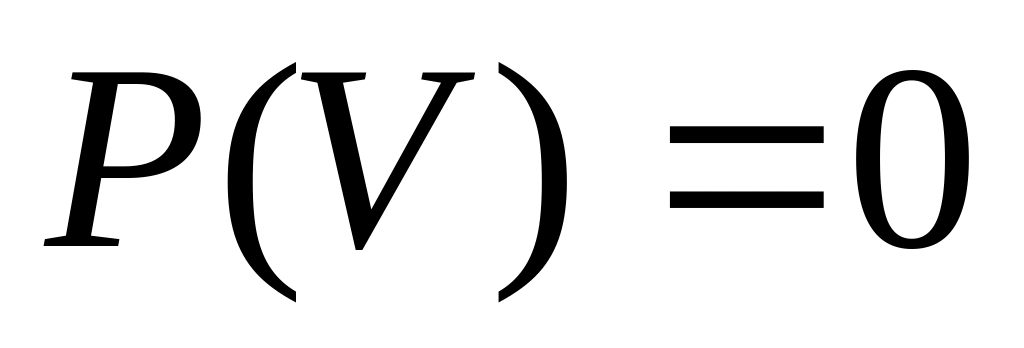 ,
, ,
,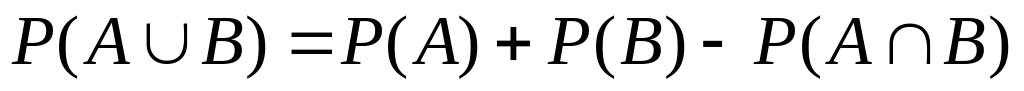 ,
,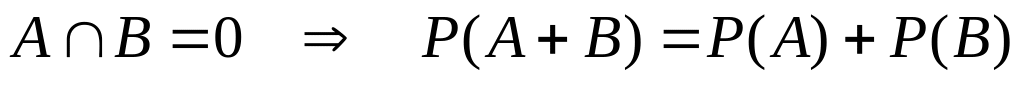 ,
, .
.
Свойства действий над событиями
 – коммутативность;
– коммутативность;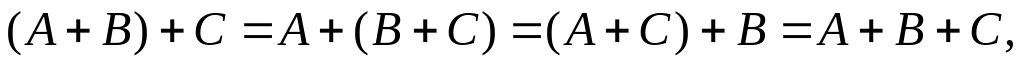
![]() – ассоциативность;
– ассоциативность;
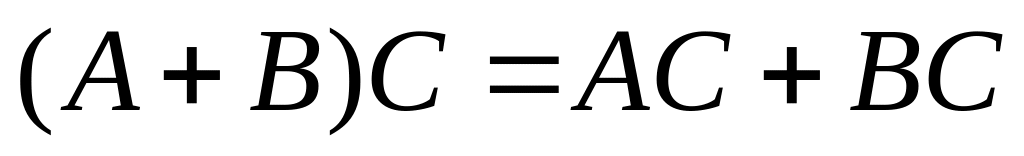 – дистрибутивность;
– дистрибутивность;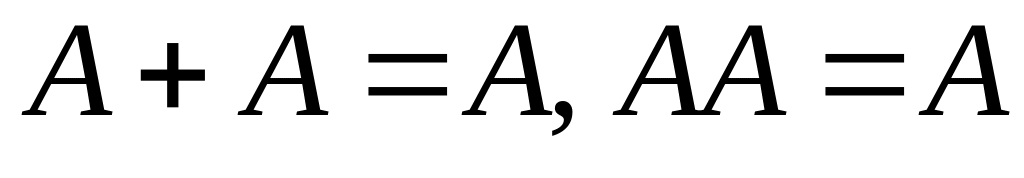 ;
;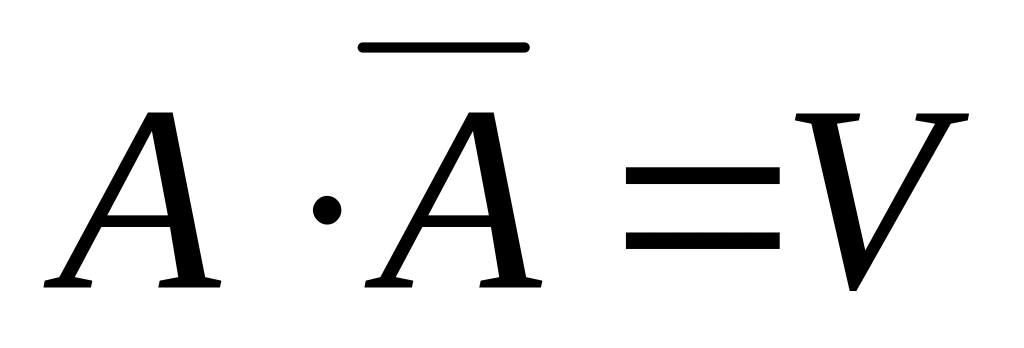 ;
;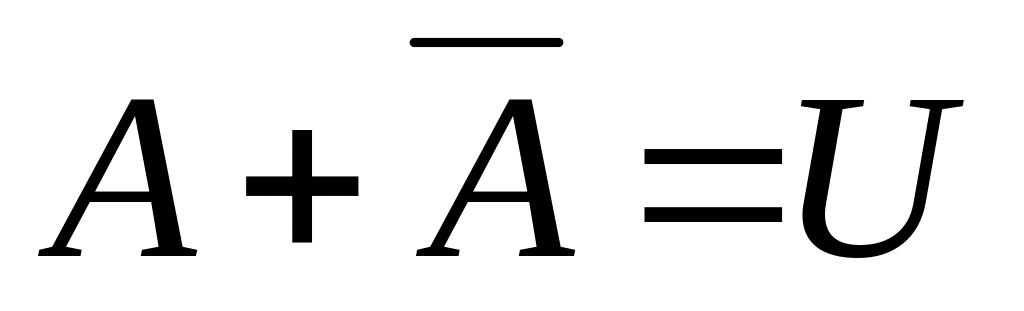 ;
;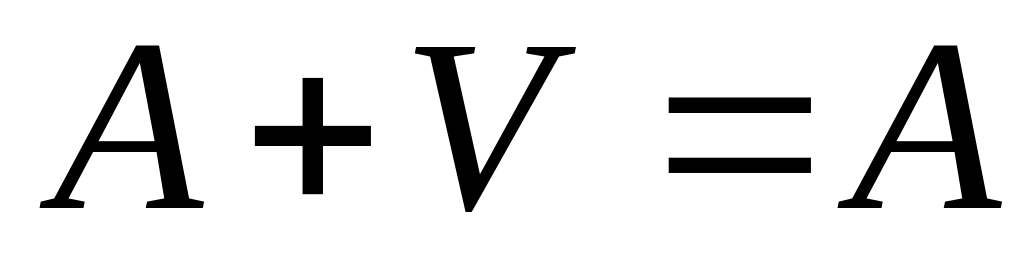 ;
; ;
; ;
; .
.
Теорема сложения вероятностей
вероятность суммы двух событий А и В можно найти по формуле:
![]() , (9)
, (9)
если события несовместны, то
![]() ; (4)
; (4)
вероятность суммы n событий:
![]() (11)
(11)
Терема умножения вероятностей
вероятность произведения двух событий
![]() ; (12)
; (12)
если события А и В независимы, то
![]() ; (5)
; (5)
вероятность произведения n событий
![]() ;
;
если события
![]() независимы
в совокупности (т.е. каждое событие из
совокупности попарно независимо с
остальными, а также со всевозможными
произведениями остальных событий), то
независимы
в совокупности (т.е. каждое событие из
совокупности попарно независимо с
остальными, а также со всевозможными
произведениями остальных событий), то
![]() .
.
Формула полной вероятности
Пусть задана полная
группа событий: {H1,H2,
…, Hn}.
Для них выполняется:
![]() .
Тогда вероятность некоторого события
А,
зависимого от H1,H2,
…, Hn
можно найти по формуле:
.
Тогда вероятность некоторого события
А,
зависимого от H1,H2,
…, Hn
можно найти по формуле:
![]() . (6)
. (6)
Формула Байеса
для событий А и В:
![]() ;
;
для полной группы событий (гипотез) вероятность гипотезы при условии, что событие А произошло, равна:
 . (7)
. (7)
Формула Бернулли
Пусть при проведении
серии n
независимых испытаний в каждом из них
событие А
происходит с вероятностью р
и не происходит с вероятностью
![]() .
Пусть при этом событие В
заключается в том, что событие А
в серии n
независимых испытаний произошло m
раз. Тогда вероятность события В
можно найти по формуле:
.
Пусть при этом событие В
заключается в том, что событие А
в серии n
независимых испытаний произошло m
раз. Тогда вероятность события В
можно найти по формуле:
![]() . (8)
. (8)
Локальная формула Муавра-Лапласа (предельная теорема Муавра-Лапласа):
 . (17)
. (17)
Формула даёт наиболее точное значение при n > 100, а npq > 20.
Исходя из формулы
Муавра-Лапласа, вероятность события В
(в серии n
независимых испытаний событие А
произошло m
раз) можно также получить, используя
функцию Гаусса (её значения приведены
в приложении Б):
![]() ,
тогда
,
тогда
![]() . (9)
. (9)
Интегральная формула Муавра-Лапласа
При большом числе испытаний в качестве события В рассматривают событие, заключающееся в том, что число успехов (наступлений события А) лежит в некотором интервале. Тогда справедлива интегральная предельная теорема Муавра-Лапласа:
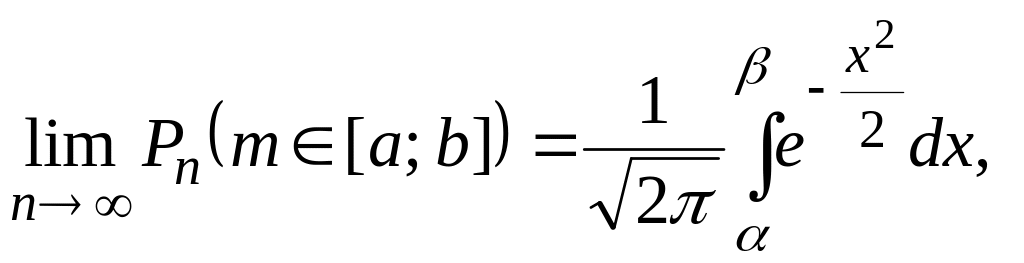 (19)
(19)

Так как значения
функции
![]() (функции Лапласа) известны (приложение
Б), то вероятность события В,
исходя из интегральной формулы
Муавра-Лапласа, находят следующим
образом:
(функции Лапласа) известны (приложение
Б), то вероятность события В,
исходя из интегральной формулы
Муавра-Лапласа, находят следующим
образом:
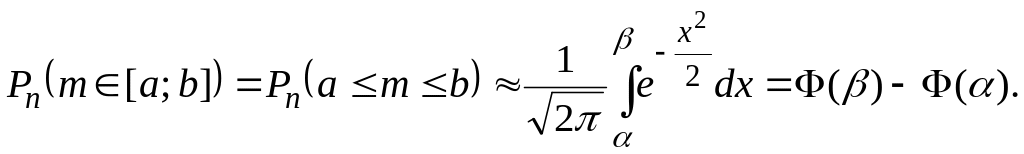 (10)
(10)
Формула Пуассона
Нахождение
вероятности события B
(в серии n
независимых испытаний событие А
произошло m
раз) по формуле Бернулли при больших
![]() затруднителен. Но в случае малой
вероятности
затруднителен. Но в случае малой
вероятности
![]() успеха, можно оценить вероятность B
следующим
образом: если
успеха, можно оценить вероятность B
следующим
образом: если
![]() и
и
![]() ,
то
,
то
![]() .
Обозначив
.
Обозначив
![]() ,
получим:
,
получим:
![]() .
(11)
.
(11)
Параметр
![]() равен среднему числу успехов в серии
из
испытаний, т.е. ожидаемому числу успехов,
где под
понимается частота успеха.
равен среднему числу успехов в серии
из
испытаний, т.е. ожидаемому числу успехов,
где под
понимается частота успеха.
Случайные величины
Случайная величина – переменная величина, которая принимает значения в зависимости от исходов испытания, т.е. случайным образом. Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены, [1, с. 57].
Дискретная случайная величина – случайная величина, принимающая конечное или счётное множество значений.
Непрерывная случайная величина – случайная величина, принимающая значения из некоторого промежутка.
Закон распределения
дискретной случайной величины
– соответствие между значениями
![]() этой величины и их вероятностями
этой величины и их вероятностями
![]() .
Закон распределения дискретной случайной
величины задаётся таблично или
аналитически:
.
Закон распределения дискретной случайной
величины задаётся таблично или
аналитически:
табличное задание (табл.1)
Таблица 1 – Закон распределения дискретной случайной величины Х
Х |
|
|
|
|
|
Р |
|
|
|
|
|
аналитическое:
![]() ,
при этом
,
при этом
![]() ,
[3, c. 52].
,
[3, c. 52].
Законы распределения дискретных случайных величин
Равномерное
распределение
– распределение случайной величины Х
с законом распределения
![]() (табличное
задание - в табл. 2).
(табличное
задание - в табл. 2).
Таблица 2 – Равномерный закон распределения дискретной случайной величины Х
Х |
|
|
|
|
|
Р |
|
|
|
|
|
При этом выполняется:
![]() .
.
Пример: Х – число выпадений герба при подбрасывании монеты.
Биномиальное распределение – распределение случайной величины Х, равной числу наступлений события А в серии n независимых испытаний. В каждом из них событие А наступает с вероятностью р и не наступает с вероятностью q = 1- p. Аналитически биномиальный закон распределения можно задать с помощью формулы Бернулли:
![]() (табличное
задание - в табл. 3)
(табличное
задание - в табл. 3)
Таблица 3 – Биномиальное распределение дискретной случайной величины Х
Х |
0 |
1 |
2 |
… |
n |
Р |
|
|
|
|
|
Геометрическое распределение – распределение случайной величины Х, равной номеру опыта, в котором первый раз наступило событие А в серии n независимых испытаний. В каждом из них событие А наступает с вероятностью р и не наступает с вероятностью q = 1 - p. Геометрический закон распределения можно задать с помощью формулы (22), табличное задание - в таблице 4.
![]() (12)
(12)
Таблица 4 – Геометрическое распределение дискретной случайной величины Х
Х |
1 |
2 |
3 |
|
n |
… |
Р |
|
|
|
|
|
… |
Гипергеометрическое распределение – распределение случайной величины Х, равной числу элементов с заданными свойствами в выборке m элементов из n. Если в выборке содержится k элементов с заданными свойствами, то гипергеометрический закон распределения можно задать с помощью формулы:
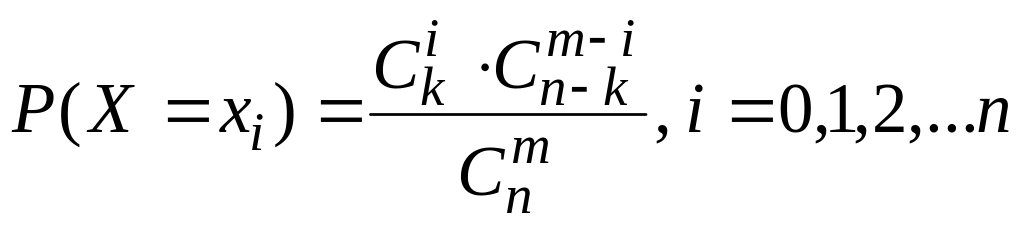 . (23)
. (23)
Законы распределения непрерывных случайных величин
Функция
распределения случайной величины F(x)
– один из видов закона распределения
случайной величины (для дискретных и
непрерывных величин). Функция распределения
принимает значения, равные вероятности
события
![]() :
:
![]() . (13)
. (13)
Функция F(x)
- неубывающая функция, принимающая
значения на интервале [0; 1]. Дискретная
случайная величина имеет счётное число
разрывов, равное n
- числу её значений. В точке разрыва
![]() функция распределения непрерывна слева.
Скачок функции F(x)
в точке разрыва равен соответствующему
значению вероятности
функция распределения непрерывна слева.
Скачок функции F(x)
в точке разрыва равен соответствующему
значению вероятности
![]() .
.
Непрерывная
случайная величина имеет непрерывную
функцию распределения, поэтому её F(x)
может иметь производную. Скачков функция
F(x)
не имеет, следовательно,
![]() .
.
Плотность распределения f(x) (плотность вероятности) случайной величины Х – производная функции распределения, так же как и её функция распределения F(x) является законом распределения непрерывной случайной величины:
![]() . (14)
. (14)
Функция f(x) неотрицательна. Для неё выполняется:
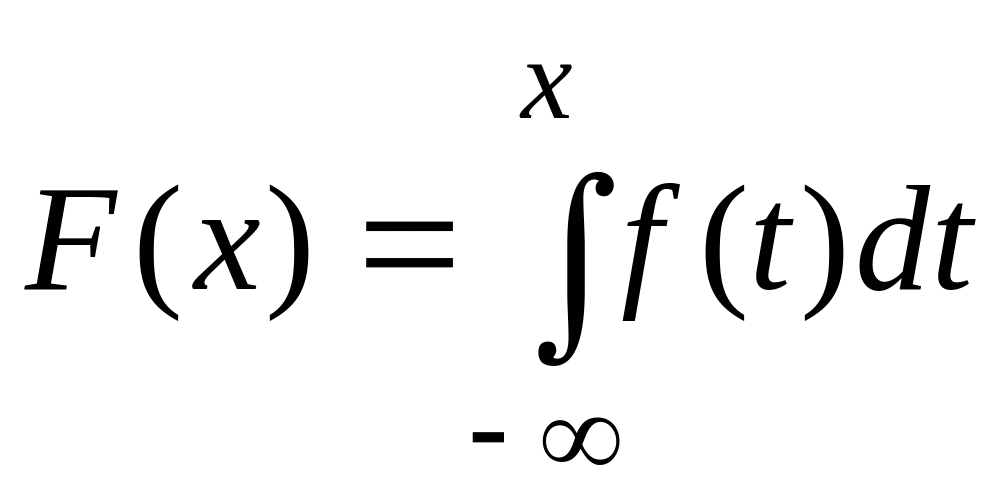 ;
; ;
; .
.
Некоторые виды законов распределения непрерывных случайных величин
Равномерное
распределение
случайной
величины Х
– распределение, для которого выполняется:
плотность распределения
![]() постоянна на
некотором отрезке и равна нулю вне этого
отрезка:
постоянна на
некотором отрезке и равна нулю вне этого
отрезка:
![]()
Так как , можно получить:
![]() (15)
(15)
Показательное распределение случайной величины Х – распределение, для которого выполняется: плотность распределения случайной величины Х имеет вид:
![]() (27)
(27)
При этом функция распределения случайной величины Х равна:
![]() (28)
(28)
Нормальное распределение случайной величины Х – распределение, для которого выполняется:
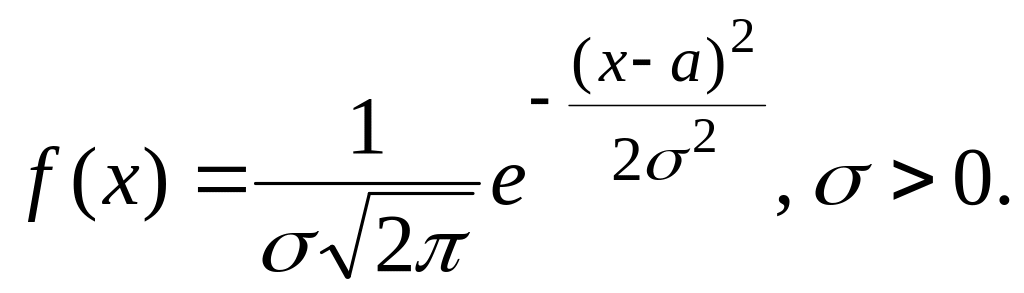 (29)
(29)
В случае нормального
распределения говорят, что непрерывная
случайная величина Х
имеет
нормальный
закон распределения (закон
Гаусса) с
параметрами а
и
![]() ,
а саму случайную величину Х
называют нормальной случайной величиной
(
,
а саму случайную величину Х
называют нормальной случайной величиной
(![]() ).
Её функцию распределения можно найти
следующим образом:
).
Её функцию распределения можно найти
следующим образом:
 (30)
(30)
Математическое
ожидание
![]() случайной
величины X
случайной
величины X
Если Х – дискретная случайная величина, то
![]() . (16)
. (16)
Если Х – непрерывная случайная величина, то
![]() . (17)
. (17)
Дисперсия
![]() случайной
величины X
случайной
величины X
![]() . (33)
. (33)
Если Х – дискретная случайная величина, то
![]() (34)
(34)
если Х – непрерывная случайная величина, то
![]() . (18)
. (18)
Среднее
квадратическое отклонение
![]() случайной
величины X
случайной
величины X
![]() . (19)
. (19)
