Плотность распределения вероятностей случайной величины и гистограмма

ТЗР-4. Плотность распределения случайной величины (дифференциальная функция распределения СВ)

Плотность распределения вероятностей СВ (другое название – дифференциальная функция распределения СВ) является очень распространенным способом задания закона распределения непрерывных СВ.

Если закон распределения непрерывной случайной величины Х задан при помощи интегральной функции F(x), то вероятность того, что СВ примет значение в интервале от х до х + Δх равна разности значений интегральной функции распределения на границах интервала:

Р(х < Х < х + Δх) = F(х + Δх) - F(х).

Вероятность, приходящаяся на единицу длины этого интервала, определится как

(F(х + Δх) - F(х))/ Δх

Если теперь устремить Δх к нулю и перейти к пределу, то получим первую производную интегральной функции распределения, которую называют плотностью распределения вероятности СВ и обозначают f(x):

lim(F(х + Δх) - F(х))/ Δх = F'(x) = f(x) (23)

Δх→0

Рассмотрим основные свойства плотности распределения вероятностей:

Свойство 1. Плотность распределения вероятностей существует только для непрерывных СВ. Для дискретных СВ производная не существует, и поэтому этот способ задания закона распределения для них неприменим.

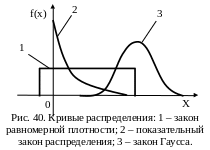Свойство 2. Плотность распределения вероятностей всегда неотрицательна:

f(x) ≥ 0, так как является производной неубывающей функции.

Свойство 3. При значениях СВ, стремящихся к ±∞, плотность распределения равна нулю или стремится к нулю.

Свойство 4. График дифференциальной функции распределения называется кривой распределения (рис. 40) и весьма нагляден (кривые для разных законов легко отличить друг от друга).

Свойство 5. Так как f(x) = F'(x), то F(x) = . (24)

Геометрически (рис. 41) интегральная функция распределения – это площадь под кривой распределения, лежащая левее точки а.

Свойство 6. Вероятность того, что случайная величина Х примет значение в интервале (а; b), есть интеграл от плотности распределения в пределах от а до b:

Р(а < Х < b) = F(b) – F(a) =

= = .

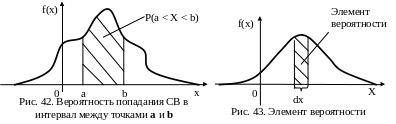Геометрически (рис. 42) вероятность попадания СВ в интервал между точками а и b – это площадь под кривой распределения, лежащая между точками а и b.

Свойство 7. Произведение f(x)dx называется элементом вероятности (рис. 43).

Свойство 8. Вся площадь, лежащая под кривой распределения, равна единице.

Это свойство несложно пояснить:

Таким образом, если в одних и тех же осях построено несколько кривых распределения, площади под ними должны быть одинаковыми. и равными единице.

Свойство 9. Размерность плотности распределения вероятностей обратна размерности случайной величины.

Это свойство можно пояснить следующим образом:

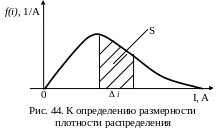Площадь под кривой распределения (рис. 44) по своему вероятностному смыслу является вероятностью. Как и всякая вероятность, эта площадь безразмерна. С другой стороны площадь есть произведение длин отрезков по осям абсцисс и ординат, т.е. по размерностям – произведение размерности СВ на размерность плотности распределения. Так, если случайной величиной является ток, измеряемый в амперах, то плотность распределения должна измеряться в 1/А – тогда произведение размерностей А ∙ 1/А даст безразмерную величину.

СтЗР-4. Гистограмма относительных частот

Статистической аналогией кривой распределения является гистограмма относительных частот. Она строится на основании группированного статистического (вариационного) ряда (табл.6).

Порядок построения гистограммы (рис.45):

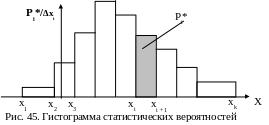1. На оси случайной величины откладываются отрезки ∆x_i, равные ширине интервалов (разрядов). Чаще всего они имеют одинаковую длину, но иногда (обычно по краям распределения) длина интервалов может быть увеличена в 2…3 раза по сравнению с центральными разрядами.

2. На отрезках ∆x_i, как на основаниях строятся прямоугольники, площади которых численно равны статистическим вероятностям р_i* попадания случайной величины в соответствующий разряд. Для того чтобы выполнить это условие необходимо правильно определить высоту каждого из прямоугольников.

Площадь каждого прямоугольника гистограммы – это статистическая вероятность P_i*=n_i/N. С другой стороны площадь прямоугольника: S_i = h_iΔx_i, где h_i – высота i-го прямоугольника гистограммы. Отсюда h_i = = .

Так как знаменатель в этом выражении для каждого разряда одинаков (при условии одинаковой их ширины), то высота h_i пропорциональна n_i. Откладывая высоты прямоугольников гистограммы в выбранном масштабе пропорционально частотам n_i.разрядов, можно существенно упростить последующий анализ статистических данных.