486

Приложение 1 математико-статистические таблицы

Методические указания к использованию таблиц

1. В ТАБЛИЦЕ 1 протабулирована функция (интеграл вероятностей) Лапласа:

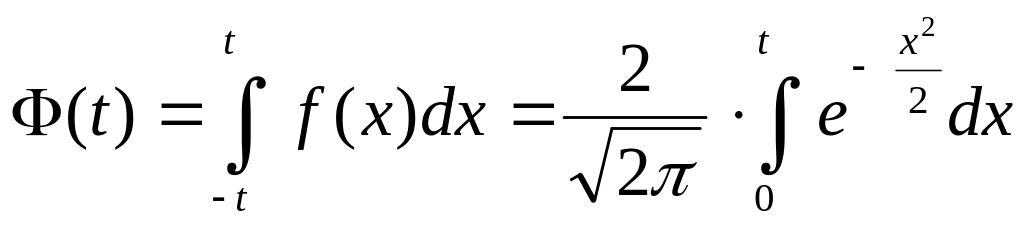
где f(t) - плотность нормированной (стандартной) нормально распределенной случайной величины T N(0,1)

Ф(t) обладает следующими свойствами:

1. Ф(t) – нечётная функция: Ф(-t) = - Ф(t);

2. Ф(t) – монотонно возрастающая функция: при t+ Ф(t) 1; Ф(+ ) = 1.

Вероятность попадания случайной величины Т в интервал от t₁ до t₂ вычисляется по формуле:

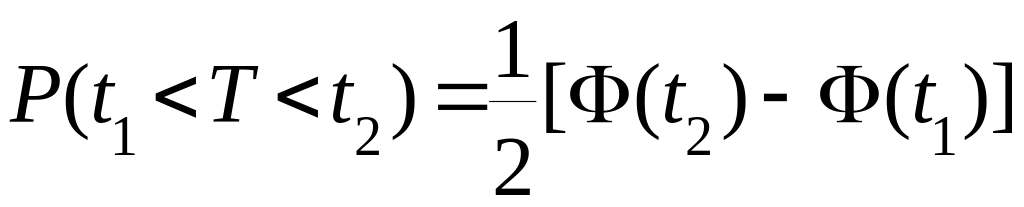
Пример 1. T N(0,1) P(-1,36<T<2,15)=?

На пересечении строки, соответствующей t=1,3 и столбца, соответствующего 6 сотым долям t, находим в середине таблицы значение функции Лапласа. Это Ф(t)= 0,8262. Таким образом, с учётом нечётности функции Лапласа, t₁=-1,36 соответствует Ф(t₁)=Ф(-1,36)=-Ф(1,36)=-0,8262.

Аналогично t₂=2,15 соответствует Ф(t₂)=Ф(2,15)=0,9684

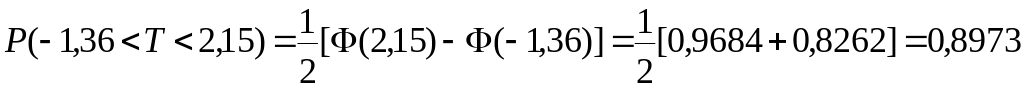
Пример 2. Ф(t)=0,98; t=?

В середине таблицы находятся значения функции Лапласа Ф(t). Находим ближайшее к 0,98 значение, это Ф(t)=0,9802. Значит, соответствующее значение t будет равно 2,33. t=2,33.

2. В ТАБЛИЦЕ 2 протабулирована вероятность выхода за пределы интервала от -t до +t случайной величины, имеющей распределение Стьюдента (t - распределение) с числом степеней свободы :

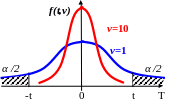
f(t;ν) - плотность распределения Стьюдента с числом степеней свободы ν.

Функция St(t) обладает следующими свойствами:

1. St(-t) = 2 - St(t);

2. St ( ) = 0; St (- ) = 2; St (0) = 1.

Вероятность попадания случайной величины T в интервал от t₁ до t₂ вычисляется по формуле:

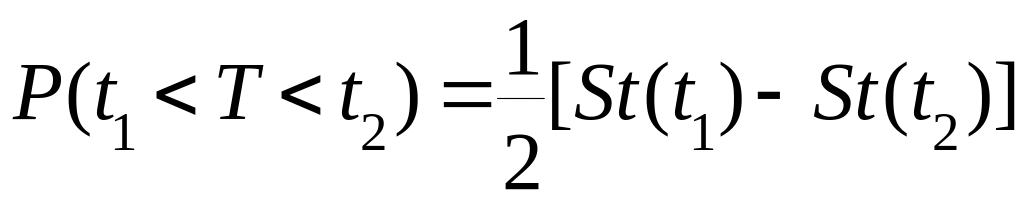
Пример 1. Для заданной вероятности α=0,05 и числа степеней свободы ν=12 найти соответствующее значение t.

На пересечении строки таблицы, соответствующей ν=12, и столбца, в котором α=0,05 , находим значение t=2,179.

Пример 2. Определить, какой вероятности α соответствует найденное значение t=1,19 при числе степеней свободы ν=8.

В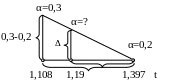 строке, соответствующей заданному числу степеней свободы ν=8, находим ближайшее значение к t=1,19 - это t=1,108, что соответствует вероятности α=0,3.

Более точно значение вероятности α можно найти методом линейной интерполяции.

Пример 3. при = 10 определить P(-1,36<T<2,15)=?

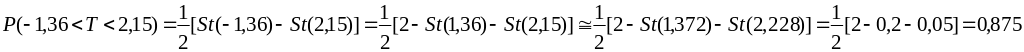Чтобы не прибегать к интерполяции, в строке, соответствующей =10, находим ближайшие к заданным значения.

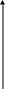3. В ТАБЛИЦЕ 3 протабулирована вероятность того, что наблюдаемое значение случайной величины χ², имеющей распределение Пирсона (хи-квадрат распределение) с числом степеней свободы n, превысит табличное значение χ²_T

На рисунке представлен график функции f(χ²,ν) - плотности c² - распределения с числом степеней свободы n.

Вероятность попадания случайной величины c² в интервал от c₁² до c₂² вычисляется по формуле

.

Функция P(c²) обладает следующими свойствами:

0 χ²_T χ²

P (0) = P(c²>0) = 1; P (+ ) = P(c²>+ ) = 0.

Пример 1. При числе степеней свободы =8 и вероятностям, равным P(c₁²)=0,975 и P(c₂²)=0,025, найти соответствующие значения c₁² и c₂².

На пересечении строки таблицы, соответствующей ν=8, и столбца, в котором P(c_T²)=0,975, находим значение c₁²=2,180. Аналогично на пересечении строки с ν=8, и столбца, в котором P(c_T²)=0,025, находим значение c₂²=17,535.

Пример 2. При числе степеней свободы =12 и значениям c₁²=3,156 и c₂²=20,48 найти соответствующие им

вероятности P(c₁²) и P(c₂²).

В строке, соответствующей заданному числу степеней свободы ν=12, находим ближайшее значение к c₁²=3,156 - это c₁²=3,074, что соответствует вероятности P(c₁²)=0,995. Аналогично в строке с ν=12, находим ближайшее значение к c₂²=20,48 - это c₂²=21,026, что соответствует вероятности P(c₂²)=0,05.

Более точно значение вероятностей P(c²) можно найти методом линейной интерполяции, приведённым в описании таблицы 2.

Пример 3. При числе степеней свободы =10 определить

Чтобы не прибегать к интерполяции, в строке таблицы, соответствующей =10, берём значения, ближайшие к заданным.

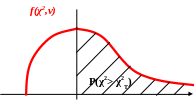
f(F)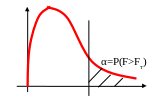

4. В ТАБЛИЦЕ 4 для случайной величины F, имеющей закон распределения Фишера-Снедекора (F-распределение) с числами степеней свободы числителя ν₁ и знаменателя ν₂, протабулированы три значения, соответствующие трем вероятностям (уровням значимости): α=P(F>F_T)=0,05 (верхнее значение); α= 0,01 (среднее значение) и α=0,001(нижнее значение).

Статистика F строится таким образом, чтобы наблюдаемое значение было не меньше единицы (числитель должен быть больше знаменателя).

П

0 F_T F

ример. Найти значение F-распределения, соответствующее уровню значимости α = 0,01 и числам степеней свободы числителя ν₁=5 и знаменателя ν₂=7.

На пересечении столбца таблицы, соответствующего числу степеней свободы числителя ν₁=5, и строки, соответствующей числу степеней свободы знаменателя ν₂=7, находим три значения F-распределения и выбираем среднее из них, соответствующее α = 0,01. Таким образом, F_T=7,46.

5. В ТАБЛИЦЕ 5 Фишера - Иейтса приведены критические значения коэффициента корреляции r_кр(α;ν) для проверки значимости генеральных парных и частных коэффициентов корреляции по выборочным.

В таблице приведены значения для четырёх уровней значимости: α=0,05; α=0,02; α=0,01 и α=0,001.

Число степеней свободы ν зависит от объёма выборки n и вида коэффициента корреляции.  = n - 2 в случае парной корреляции и  = n - l - 2, где l - число исключенных величин, в случае частной корреляции.

Пример. Найти критические значения коэффициента корреляции r_кр(α;ν) для проверки значимости

r_кр(α=0,02; ν=21) находится на пересечении строки таблицы, соответствующей ν=21 и столбца со значением α=0,02 в верхней части таблицы (для двусторонних границ). ν=21 отсутствует, поэтому методом линейной парных и частных коэффициентов корреляции в случае трёхмерной модели (X,Y,Z) на уровне значимости α=0,02, если число наблюдений, по которым рассчитаны выборочные коэффициенты корреляции, равно n=23.

При проверке значимости парных коэффициентов корреляции ρ_xy, ρ_yz, ρ_xz число степеней свободы  =n-2=21. интерполяции находим недостающее значение r_кр для ν=21 между r_кр=0,492 (для ν=20) и r_кр=0,445 (для ν=25). Повышение степени свободы на 1 соответствует понижению r_кр на (0,492-0,445)/5=0,0094; следовательно, r_кр(ν=21)=0,492-0,0094=0,4826. Таким образом, для парных коэффициентов корреляции r_кр=0,4826.

При проверке значимости частных коэффициентов корреляции ρ_xy/z, ρ_yz/x, ρ_xz/y число степеней свободы =n-l-2=23-1-2=20 (l=1 в случае трёхмерной модели, фиксируется одна переменная). r_кр(α=0,02; ν=20) находится на пересечении строки таблицы, в которой ν=20 и столбца со значением α=0,02 в верхней части таблицы (для двусторонних границ). Таким образом, для частных коэффициентов корреляции r_кр=0,492.

6. В ТАБЛИЦЕ 6 приведены значения прямого и обратного Z-преобразования Фишера, соответствующие гиперболическим арктангенсам и гиперболическим тангенсам заданных чисел.

;

Используются в математической статистике при расчёте интервальных оценок генеральных коэффициентов корреляции. Для значимых выборочных парных и частных коэффициентов корреляции можно построить с заданной надёжностью γ доверительный интервал ρ_min ≤ ρ ≤ ρ_max с помощью Z-преобразования Фишера:

;

Пример. Для выборки из 15 наблюдений двумерной нормальной совокупности (X,Y) получено, что выборочный коэффициент корреляции равен r=-0,85. С надёжностью γ=0,95 построить доверительный интервал для генерального коэффициента корреляции ρ_min ≤ ρ ≤ ρ_max.

1). По найденному выборочному коэффициенту корреляции r=0,85 с помощью таблицы 6 находим соответствующее значение Z_r на пересечении строки, в которой r=0,8 и столбца, соответствующего 5 сотым долям r. Таким образом, получаем Z_r=-1,2562. (Z(-r)=-Z(r) , т.к. Z(r) - функция нечётная)

2). Вычисляем (t_γ=1,96 , соответствующее заданной надёжности γ=0,95 , находим по таблице 1 функции Лапласа для Ф(t_γ)=γ=0,95).

Затем рассчитываем Z_min = Z_r – ΔZ=-1,2562-0,5658=-1,822; Z_max= Z_r + ΔZ=-1,2562+0,5658=-0,6904.

3). Соответствующие значения ρ_min и ρ_max находятся с помощью обратного преобразования Фишера следующим образом. В середине таблицы 6 находим ближайшие к рассчитанным Z_min и Z_max значения и определяем, каким коэффициентам корреляции они соответствуют.

Z_min=-1,822; в середине таблицы 6 находим ближайшее значение, это Z=1,8318. Это соответствует коэффициенту корреляции, равному 0,95 (смотрим, на пересечении каких строки и столбца находится найденное значение Z). Следовательно, нижняя граница генерального коэффициента корреляции ρ_min=-0,95.

Аналогично для Z_max=-0,6904 в середине таблицы 6 находим ближайшее значение, это Z=0,6932. Это соответствует коэффициенту корреляции, равному 0,60. Следовательно, верхняя граница генерального коэффициента корреляции ρ_max=-0,60. (Более точно значения ρ_min и ρ_max можно получить, рассчитав по формуле гиперболического тангенса, приведённой выше). Таким образом, Р(-0,95≤ ρ ≤ -0,60)= γ=0,95.

7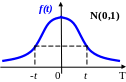 . В ТАБЛИЦЕ 7 протабулирована функция плотности вероятностей (функция Гаусса) f(t) нормирован-ной (стандартной) нормально распределенной случайной величины T N(0,1)

f(t) обладает следующими свойствами:

1. f(t) – чётная функция: f(-t) = f(t). Функция f(t) симметрична относительно оси ординат

2. f(t) – монотонно убывающая функция: при t± f(t) 0; f(+ ) = 0.

Пример 1. T N(0,1); t=1,53; f(t)=?

На пересечении строки, соответствующей t=1,5 и столбца, соответствующего 3 сотым долям t, находим в середине таблицы значение функции Гаусса f(t)=0,1238.

Пример 2. T N(0,1); f(t)=0,31; t=?

В середине таблицы находим значение функции Гаусса, ближайшее к заданному 0,31. Это f(t)=0,3101. Теперь смотрим, какому t это соответствует, т.е на пересечении каких строки и столбца находится найденное значение f(t). Таким образом, получаем t=0,71.

8. В ТАБЛИЦЕ 8 протабулированы значения функции Пуассона вероятности того, что в n повторных независимых испытаниях событие А наступит ровно m раз. Формула Пуассона используется при вероятности наступления события p, близкой к нулю, и параметру λ=np, находящемуся в пределах 0,1 ≤ λ ≤ 10.

Пример. Событие А происходит в каждом из испытаний с вероятностью p=0,005. Найти вероятность, что при проведении 1000 испытаний событие А наступит 3 раза.

n=1000; m=3; p=0,005. P₁₀₀₀(X=3)=?

λ=np=1000·0,005=5. Искомую вероятность находим в таблице 8 на пересечении строки, соответствующей m=3 и столбца, в котором λ=5. Таким образом, P₁₀₀₀(X=3)= 0,1404.

9. В ТАБЛИЦЕ 9 приведены значения G – распределения. Используется в математической статистике при проверке гипотезы об однородности ряда дисперсий k генеральных совокупностей с помощью критерия Кохрана. Значения G – распределения приводятся в таблице для двух уровней значимости. Первое значение соответствует уровню значимости  = 0,05, а второе -  = 0,01.

Кроме того, значение G зависит от числа степеней свободы ν= n-1 (где n – объём независимых выборок из каждой совокупности) и количества рассматриваемых совокупностей k, для которых проверяется равенство генеральных дисперсий.

Пример. Для проверки гипотезы о равенстве генеральных дисперсий 4 совокупностей осуществили независимые выборки по 10 наблюдений в каждой. Критерий Кохрана проверяется на уровне значимости =0,05. Найти соответствующее значение G-распределения G_кр .

На пересечении строки таблицы 9, соответствующей k=4, и столбца, в котором число степеней свободы ν=n-1=10-1=9 находятся два значения G-распределения. Берём верхнее из них, соответствующее заданному уровню значимости =0,05. Таким образом, G_кр=0,502.

Таблица 1