Квадратурные формулы Ньютона-Котеса

Частный случай интерполяционных квадратурных формул, когда на , а - равноотстоящие узлы с шагом , где , , , .

Рассмотрим выражение для коэффициентов , интерполяционной квадратурной формулы (3).

Выполним в формуле (4) замену переменной интегрирования: . Перейдем от к ; , получим:

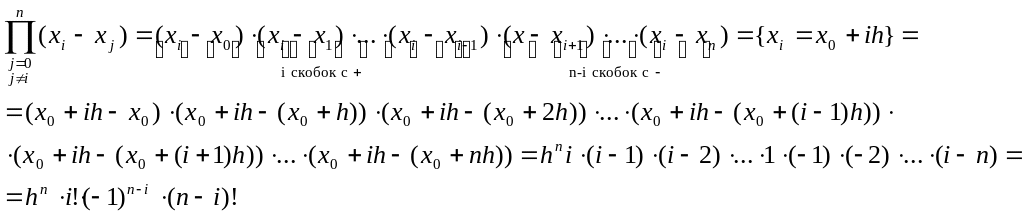
Подставив в (4) получаем:

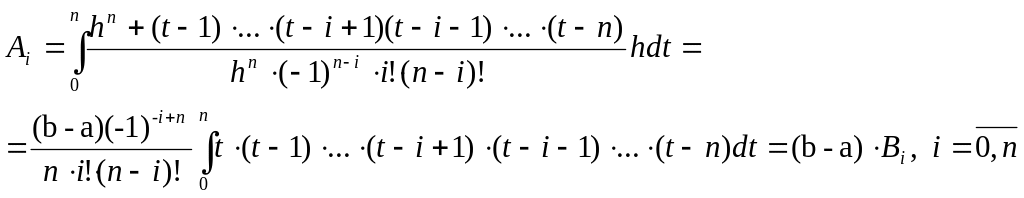
, (7).

Коэффициенты называются коэффициентами Котеса. Подставляя в формулу (1) получим: (8) – квадратурная формула Ньютона-Котеса с коэффициентами (7) в качестве узлов – равноудаленные точки.

Свойства коэффициентов Котеса

1. Коэффициенты , не зависят от отрезка интегрирования и величины шага, поэтому для достаточно больших они заранее посчитаны и приводятся в специальной литературе.

При

При

При и т.д.

2. Коэффициенты Котеса симметричны относительно середины промежутка интегрирования.

3. .

Частные случаи формул Ньютона-Котеса

1. при :

- один узел в квадратурной формуле (8). При этом формулой (7) для коэффициентов Котеса воспользоваться нельзя, поскольку она содержит неопределенность.

Поэтому будем строить формулу для любых коэффициентов исходя из общей идеи построения интерполяционных квадратурных формул.

Заменим подынтегральную функцию ее интерполяционным многочленом, построенным по единственному узлу . Получим:

, , .Тогда , (9) – квадратурная формула прямоугольника,

причем, если , то формула (9) называется квадратурной формулой левых прямоугольников, если , то (9) – квадратурная формула правых прямоугольников, если , то (9) – квадратурная формула средних прямоугольников.

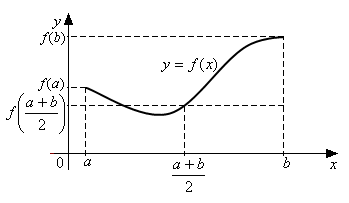
Рассмотрим погрешность квадратурной формулы левых прямоугольников:

. С другой стороны из общей формулы (5) имеем: , .

На основе теоремы о среднем значении получаем: найдется такая точка , что , (10).

Остаточный член квадратурной формулы правых прямоугольников при так же имеет представление (10).

Рассмотрим остаточный член квадратурной формулы средних прямоугольников.

, получим: (11).

Тогда из формулы (5): .

Очевидно, что в этом случае нельзя применить теорему о среднем значении, так как функция меняет свой знак.

Разложим подынтегральную функцию в ряд Тейлора в окрестности точки :

, где , .

Перенесем в левую часть и проинтегрируем на промежутке :

, где (на основании теоремы о среднем).

, (12).

Рассмотренные нами разновидности формулы прямоугольников (9) носят название элементарных формул прямоугольников.

Но если отрезок достаточно велик, то рассмотренные элементарные формулы имеют не высокую точность.

В этом случае строят так называемые составные (полные) квадратурные формулы.

Отрезок интегрирования разбивают на ( - достаточно большое натуральное число) равных частей с шагом и получают точки разбиения , .

И на каждом частичном промежутке , применяется та или иная квадратурная формула.

Пример. , .

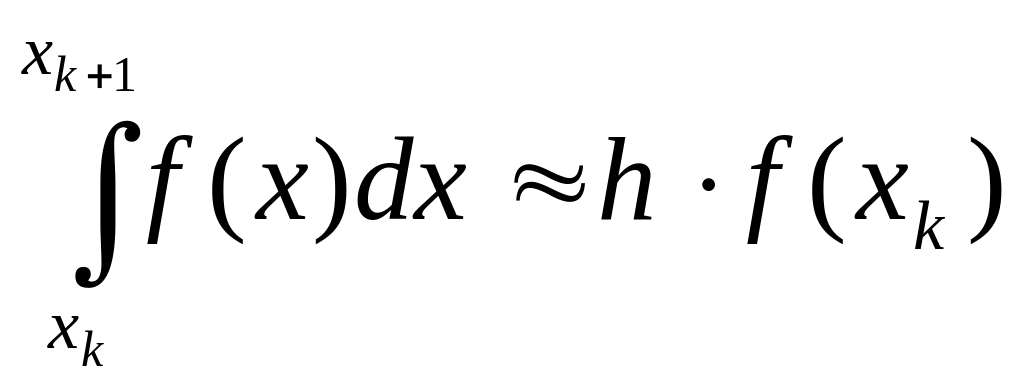Просуммируем по всем - (13) полная формула левых прямоугольников.

Аналогично можно построить полные формулы правых и средних прямоугольников:

- (14) полная формула правых прямоугольников, - (15) полная формула средних прямоугольников.

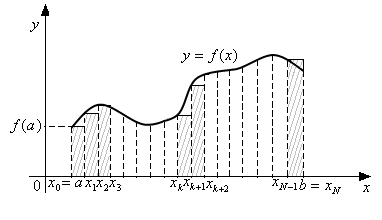
Остаточные члены полных формул прямоугольников (13), (14), (15) получим в результате суммирования погрешностей, полученных на каждом частичном промежутке .

Формулы остаточных членов имеют вид: (16), - остаточный член формул (13) и (14).

Заметим, что , , .

Чем меньше , тем меньше погрешность. При .

(17), - остаточный член формулы (15).

Замечание. Сравнивая остаточные члены (16) и (17) видим, что при одинаково малом полная формула средних прямоугольников более точная, чем полная формула левых и правых прямоугольников, например, при , , .

Кроме того, заметим, что формулы правых и левых прямоугольников дают точный результат ( ) лишь при .

А формула средних прямоугольников будет так же точна для любого многочлена первой степени.

Отсюда следует, что алгебраическая степень точности квадратурных формул левых и правых прямоугольников равна 0, а алгебраическая степень точности формулы средних прямоугольников равна 1.

2. при : ; ; .

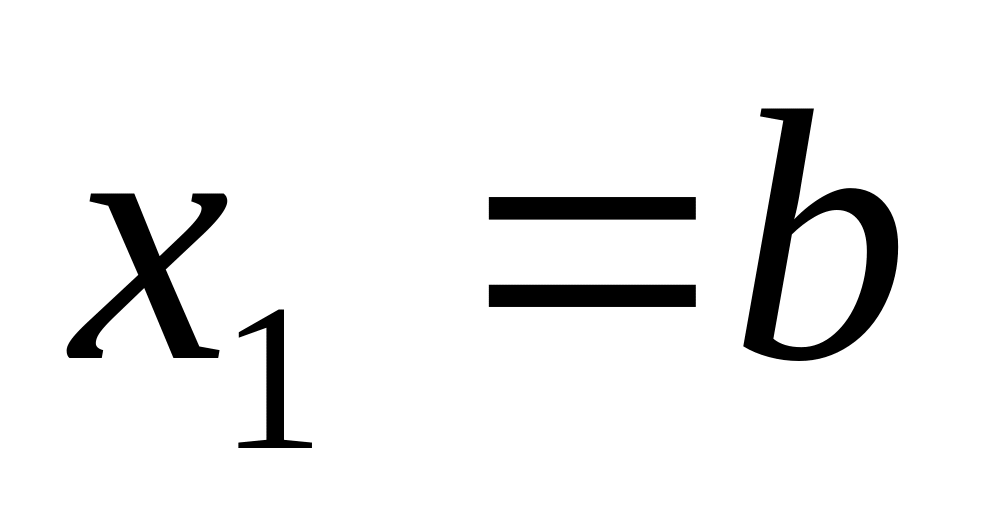(18).

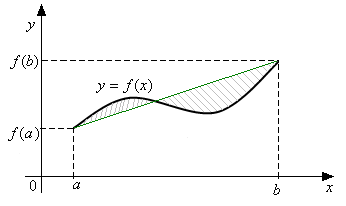
Погрешность квадратурной формулы (18) выводится из формулы (5):

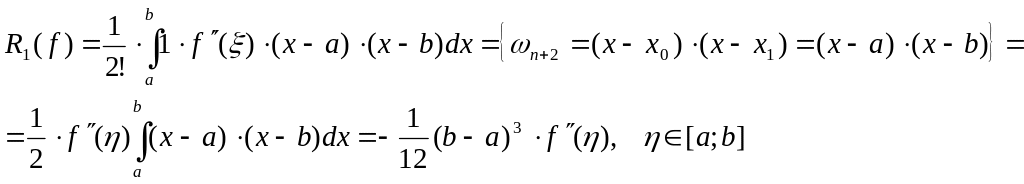(19)

Построим полную формулу.

Разобьём отрезок интегрирования на равных частей с шагом , , .

, ,

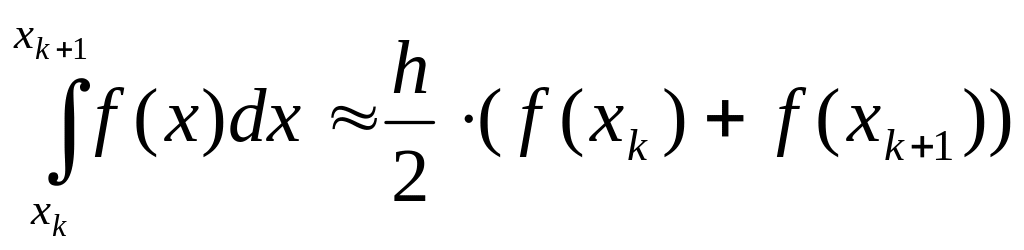(20) - составная формула трапеции.

Её остаточный член имеет следующий вид: , (21).

Замечание. Сравнивая формулы (21) и (17) видим, что формулы трапеции и средних прямоугольников имеют одинаковые точности по , а так же одинаковую алгебраическую степень точности, равную 1.

3. при : ; ; ; , .

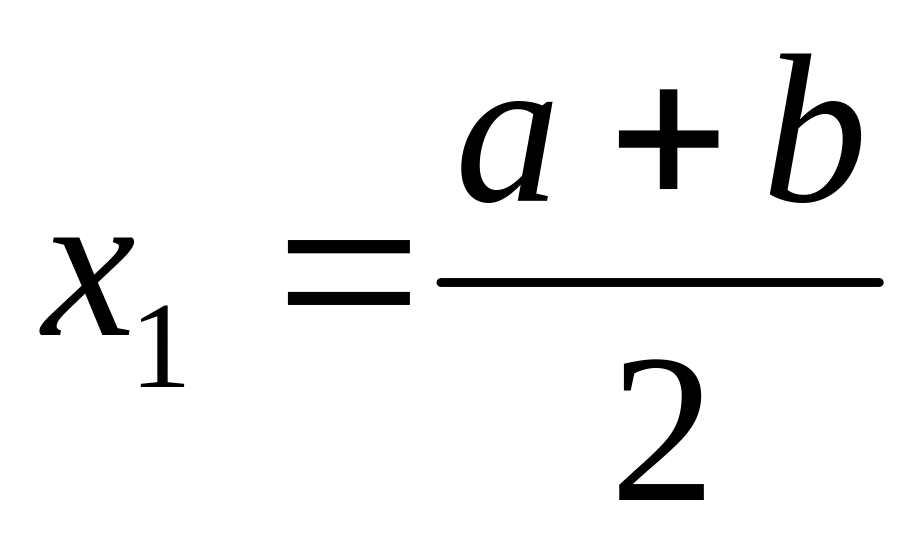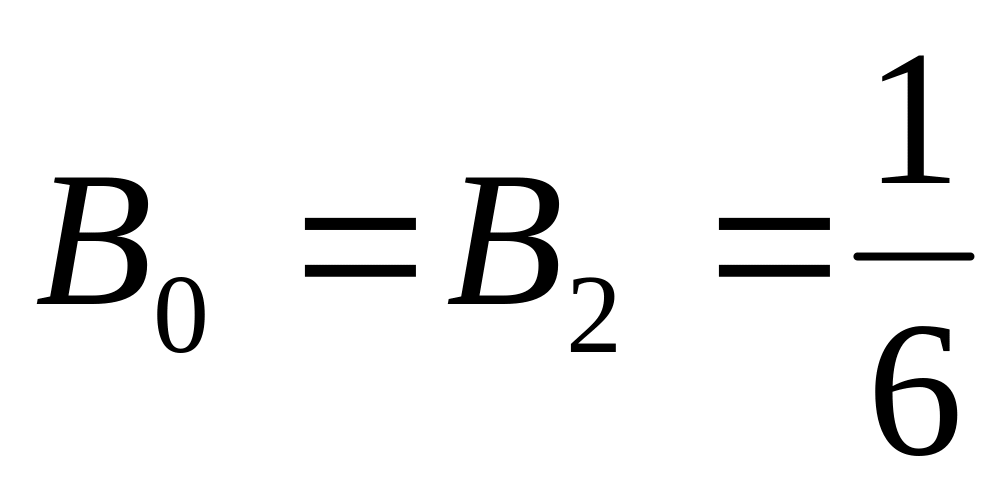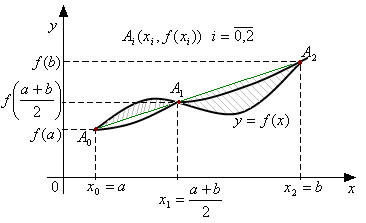
(22) – элементарная квадратурная формула Симпсона (формула параболы).

Остаточный член имеет вид: (23), - остаточный член элементарной формулы параболы.

Рассмотрим составную формулу Симпсона.

Разобьем отрезок интегрирования на четное число частей с шагом , - равноотстоящие с шагом .

На каждом частичном промежутке , содержащем 3 точки применим элементарную формулу Симпсона (22), .

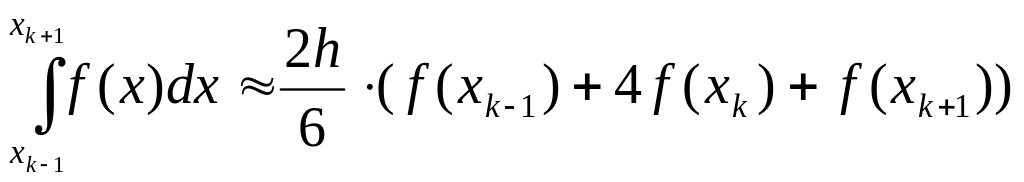
Просуммировав эти примерно равные по всем номерам , получим:

(24) – составная квадратурная формула Симпсона.

Остаточный член имеет вид: (25), .

Заметим, что из формул (23) и (25) следует, что формула Симпсона и в элементарном и в составном варианте будет точна ( ) для всех многочленов 3-ей степени. То есть алгебраическая степень точности формулы Симпсона равна 3.

Замечание о точности квадратурных формул

Точность рассмотренных нами квадратурных формул существенно зависит от выбора узлов . Если подынтегральная функция сильно извилиста, то есть имеет много нулей и много экстремумов, то в этом случае шаг интегрирования надо выбирать намного меньше расстояний между соседними нулями и экстремумами функции.