
- •Лекции по курсу: «численные методы»
- •Приближение функций
- •Численное интегрирование
- •Квадратурные формулы Ньютона-Котеса
- •Частные случаи формул Ньютона-Котеса
- •Квадратурные формулы наивысшей алгебраической степени точности (н.А.С.Т.)
- •Квадратурная формула Гаусса (частный случай квадратурной формулы н.А.С.Т. При )
- •Смысл введения весовой функции
- •Приближённое решение алгебраических и трансцендентных уравнений
- •Методы решения систем линейных алгебраических уравнений (слау)
- •Приближённое решение проблемы собственных значений матрицы
Методы решения систем линейных алгебраических уравнений (слау)
Необходимые вспомогательные сведенья из математического анализа и алгебры
Обозначим через
![]() -мерное,
вещественное, векторное, линейное
пространство. Если
-мерное,
вещественное, векторное, линейное
пространство. Если
![]() ,
то
,
то
![]() .
.
Скалярное произведение
векторов вычисляется по формуле:
![]() ,
где
,
где
![]() и
и
![]() .
.
Определение.
Нормой вектора
![]() называется вещественное число, условно
обозначаемое
называется вещественное число, условно
обозначаемое
![]() ,
удовлетворяющее следующим аксиомам:
,
удовлетворяющее следующим аксиомам:
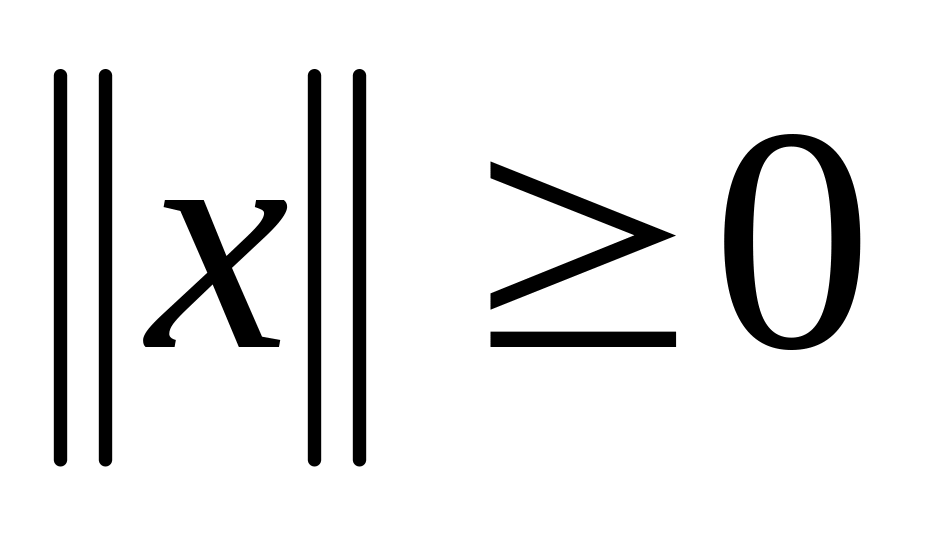 и
и
 ;
;свойство однородности:
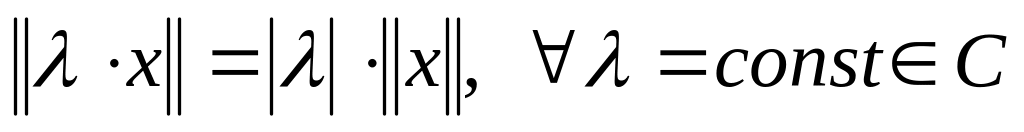 ;
;равенство треугольника:
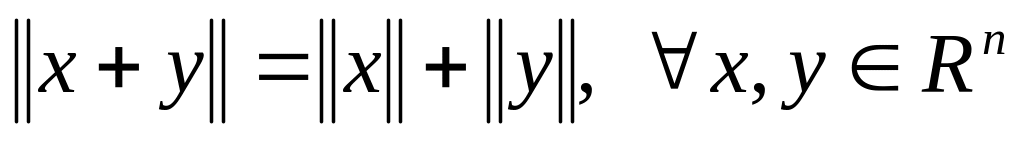 .
.
Существуют несколько способов вычисления нормы вектора. Наиболее известные следующие:
кубическая норма:
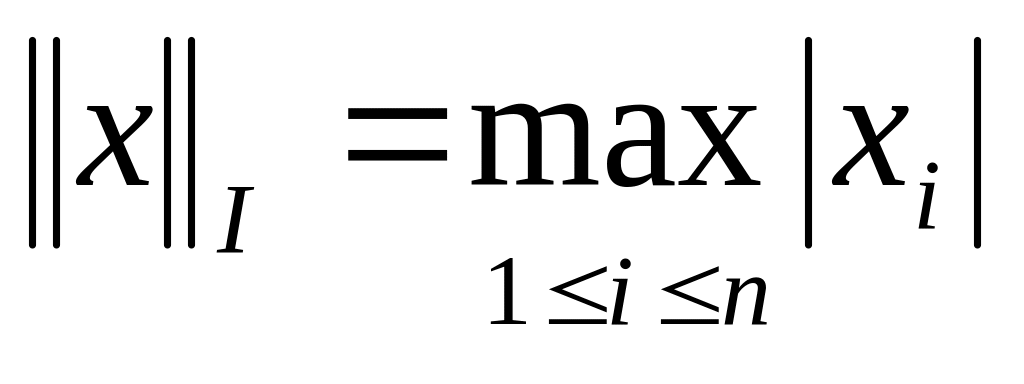 ;
;октаэдрическая норма:
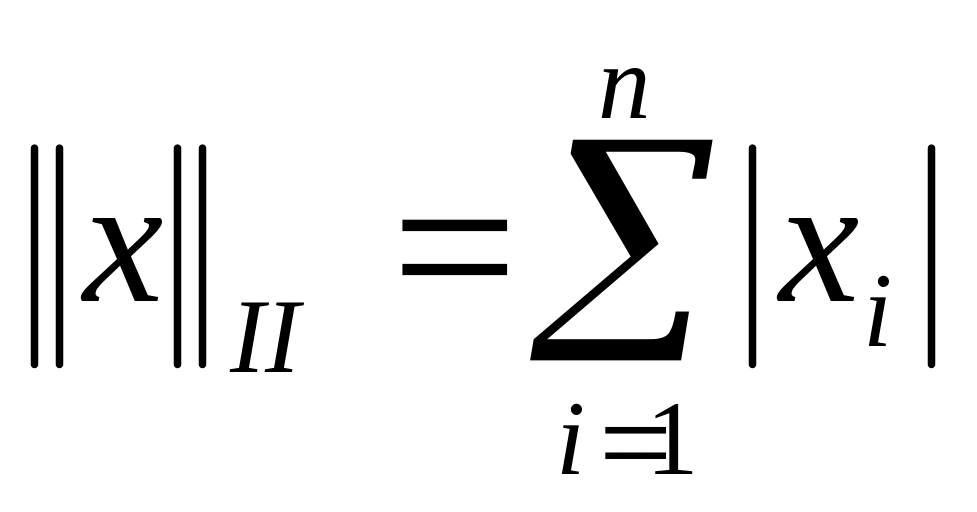 ;
;Эвклидова (сферическая) норма:
 .
.
Пусть
![]() - квадратная матрица
-го
порядка.
- квадратная матрица
-го
порядка.
Определение.
Нормой матрицы
![]() называется вещественное число, условно
обозначаемое
называется вещественное число, условно
обозначаемое
![]() ,
удовлетворяющее следующим аксиомам:
,
удовлетворяющее следующим аксиомам:
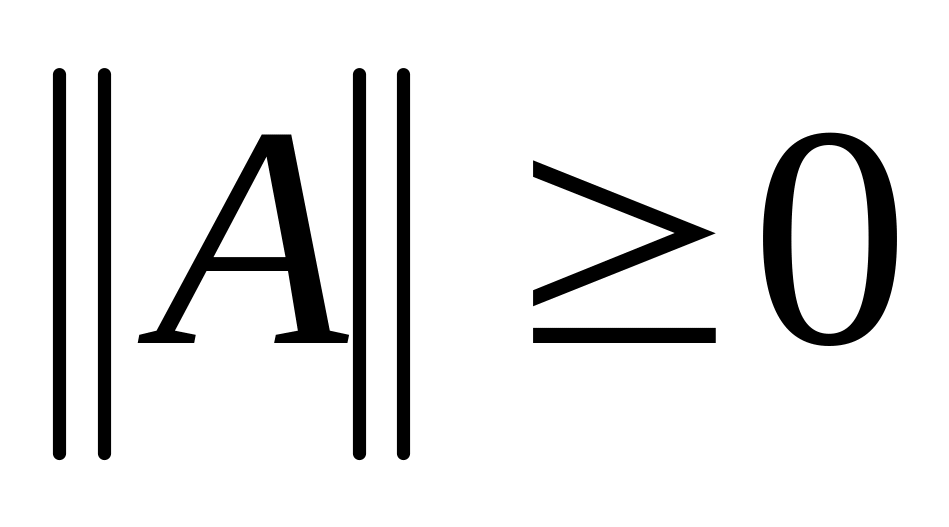 и
и
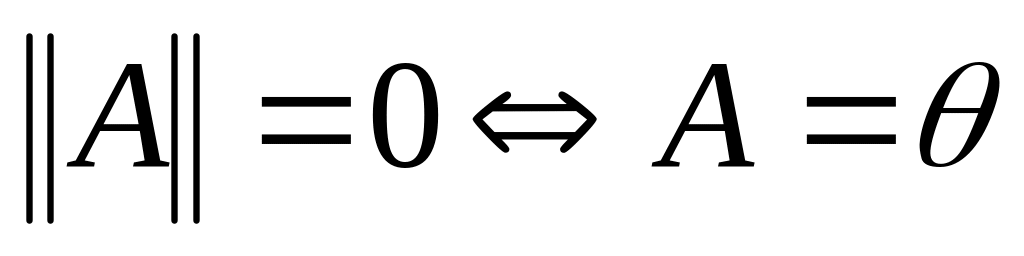 ;
;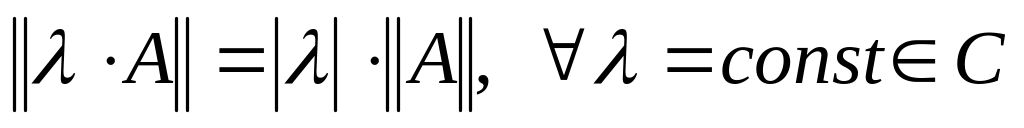 ;
; ,
и
,
и
 имеют одинаковый порядок;
имеют одинаковый порядок;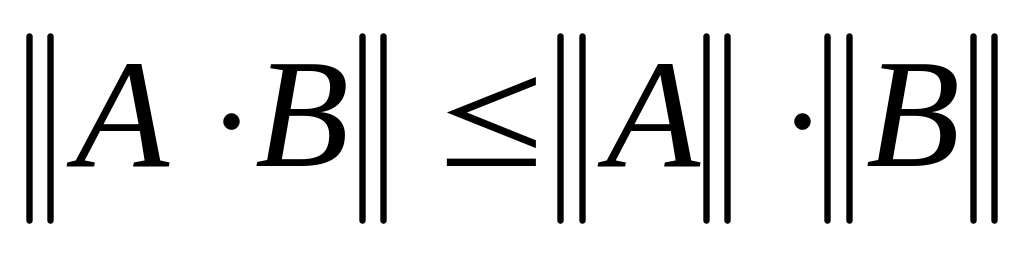
Норма квадратной
матрицы
называется согласованной с данной
нормой вектора
![]() ,
если для
,
если для
![]() выполняется следующее неравенство:
выполняется следующее неравенство:
![]() (1).
(1).
Определение. Согласованная норма называется подчинённой данной норме вектора, если для в неравенстве (1) достигается знак равенства (подчинённая – наименьшая из всех согласованных норм).
Можно показать, что:
![]() (2).
(2).
Приведём наиболее распространённые нормы матриц:
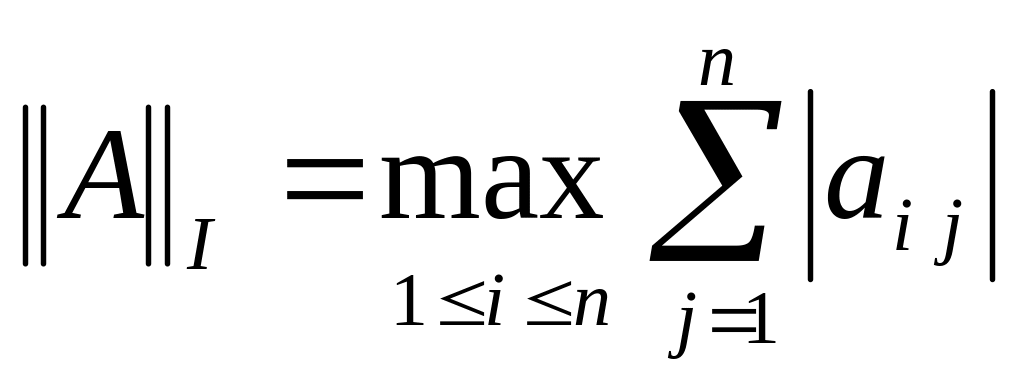 -
подчинена
-
подчинена
 ;
;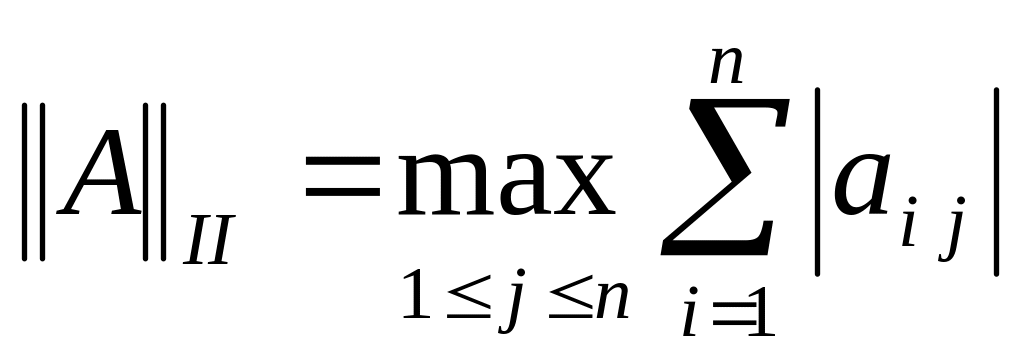 -
подчинена
-
подчинена
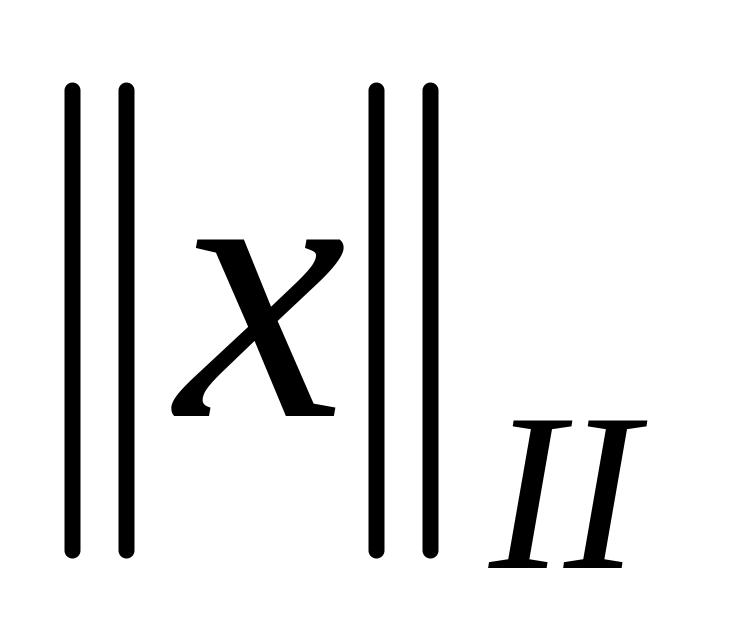 ;
;спектральная норма:
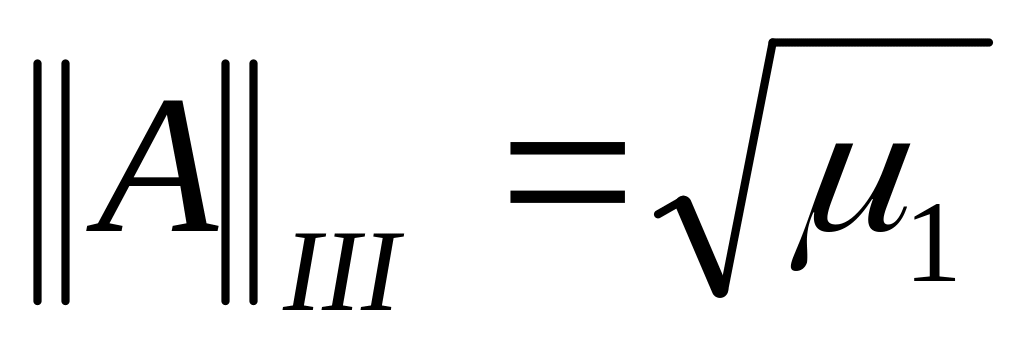 ,
где
,
где
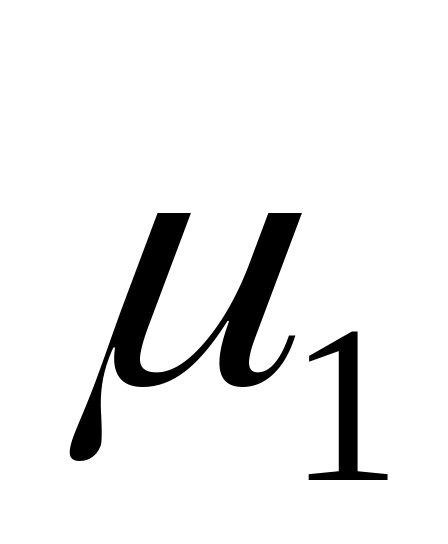 -
наибольшее по модулю собственное
значение матрицы
-
наибольшее по модулю собственное
значение матрицы
 ,
где
,
где
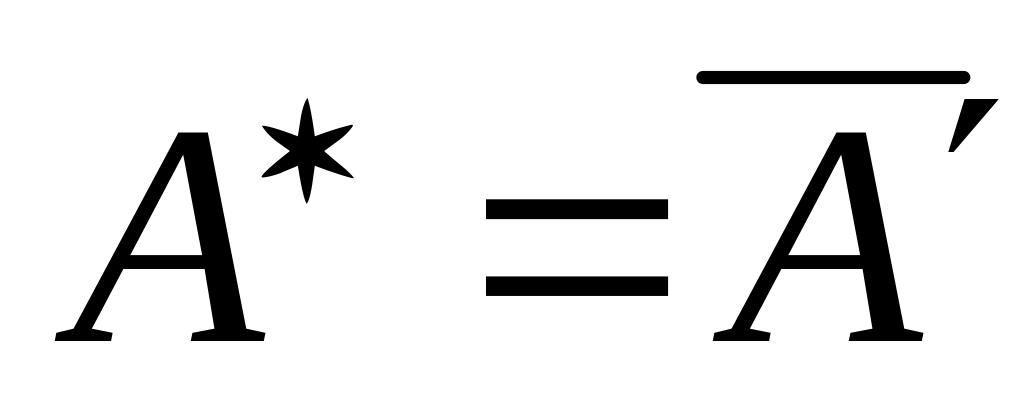 -
транспонированная, комплексно-сопряжённая.
-
транспонированная, комплексно-сопряжённая.
Данная норма матрицы
подчинена
![]() .
.
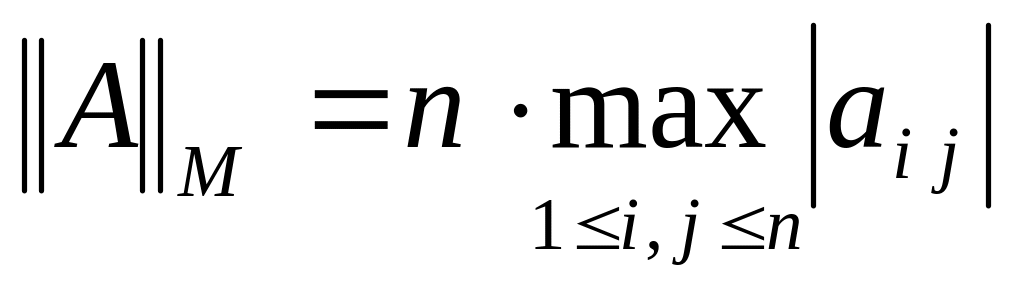 -
согласована с
,
,
;
-
согласована с
,
,
;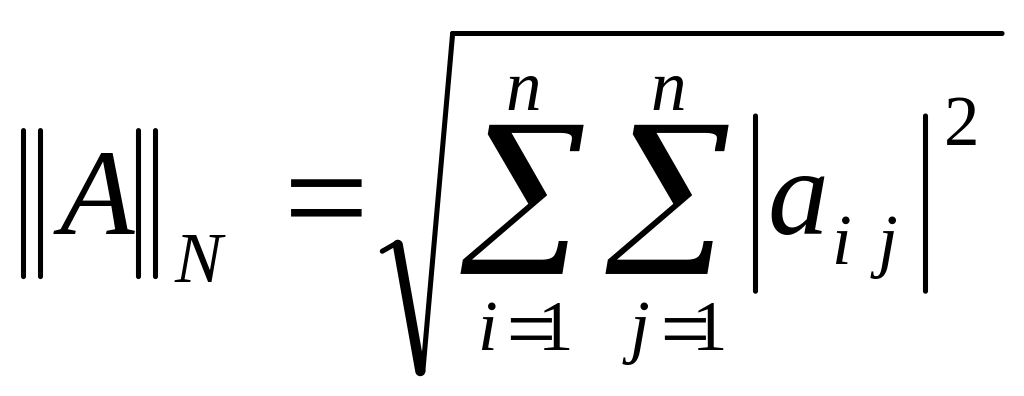 -
норма Шмидта, согласована с
.
-
норма Шмидта, согласована с
.
Замечание.
Легко заметить из формулы (2),
что подчинённая норма единичной матрицы
![]() :
:
![]() ,
,
![]() .
.
Определим понятия сходимости векторных и матричных последовательностей.
Пусть имеется
последовательность векторов
![]() в
в
![]() ,
то есть
,
то есть
![]() и пусть имеется вектор
и пусть имеется вектор
![]() .
Будем говорить, что последовательность
векторов
сходится
к вектору
в
,
если для любого номера координаты
.
Будем говорить, что последовательность
векторов
сходится
к вектору
в
,
если для любого номера координаты
![]() имеет место покоординатная сходимость:
имеет место покоординатная сходимость:
![]() .
.
Аналогично, пусть
имеется последовательность матриц
![]() ,
то есть
,
то есть
![]() и пусть имеется матрица
.
Будем говорить, что матричная
последовательность
сходится
к матрице
,
если для любых номеров координат
и пусть имеется матрица
.
Будем говорить, что матричная
последовательность
сходится
к матрице
,
если для любых номеров координат
![]() выполняется условие:
выполняется условие:
![]() .
.
Теорема 1.
Для того чтоб последовательность
векторов
сходилась
к вектору
в
необходимо и достаточно чтоб
![]() .
.
Теорема 2.
Для того чтоб матричная последовательность
сходилась
к матрице
необходимо и достаточно чтоб
![]() .
.
Замечание. Формулировка теорем 1 или 2 векторной и матричной нормы произвольны.
Пусть задана СЛАУ:
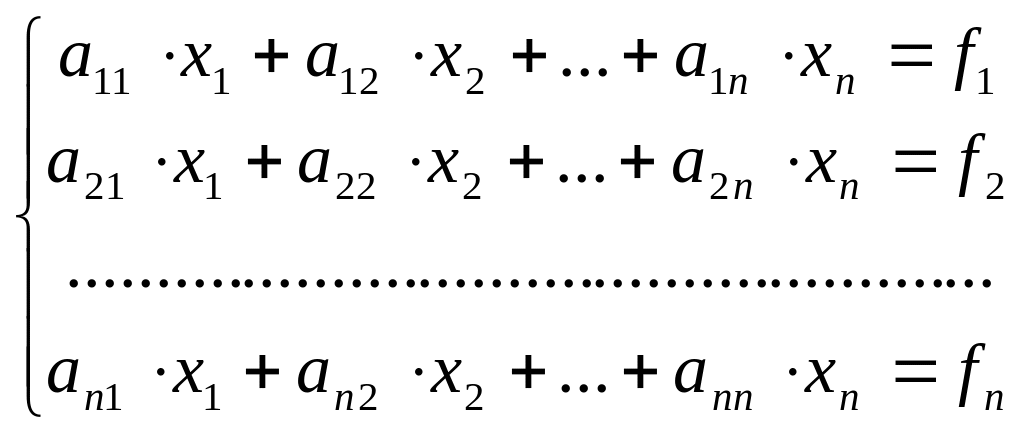 (3).
(3).
Введём обозначения:
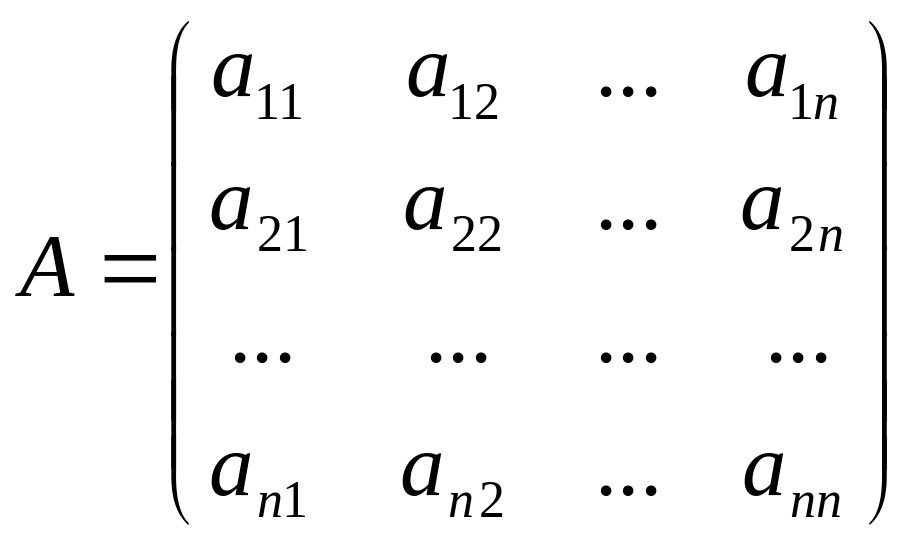 -
матрица коэффициентов;
-
матрица коэффициентов;
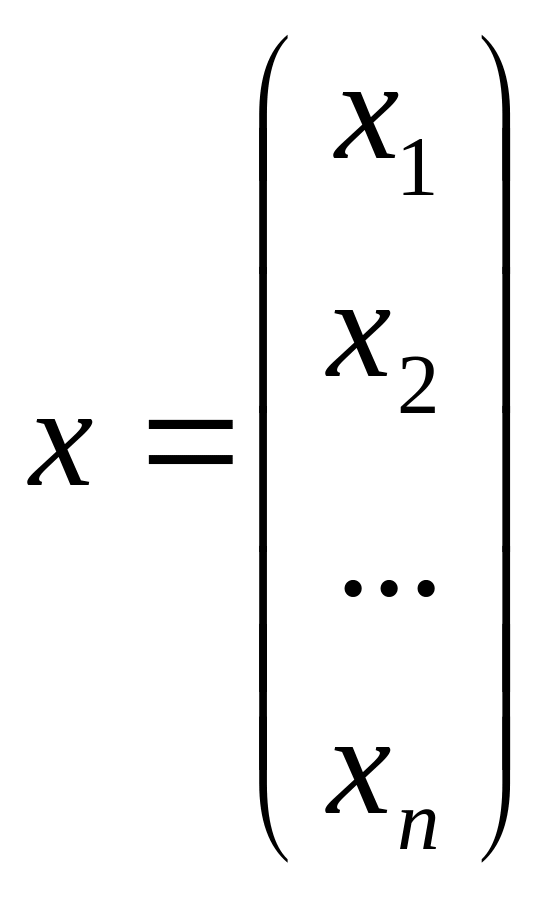 -
столбец неизвестных;
-
столбец неизвестных;
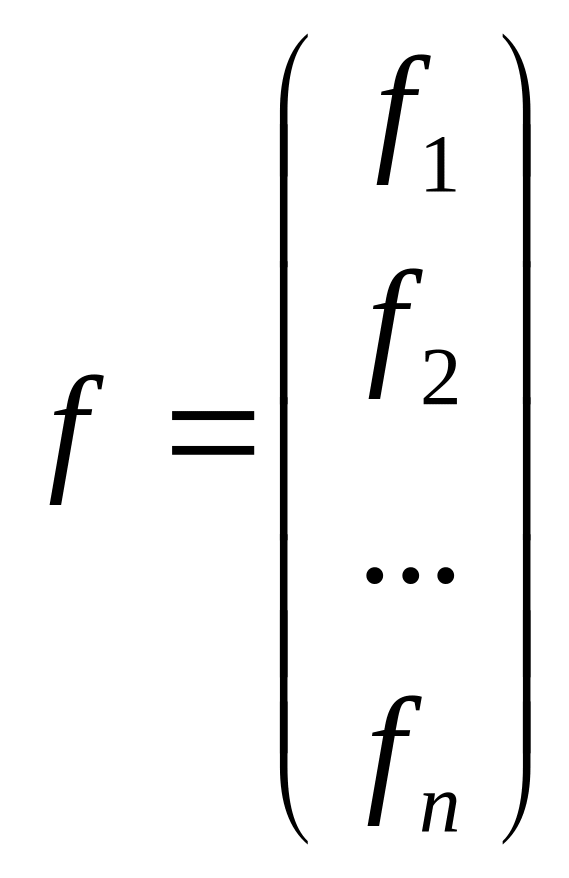 -
столбец свободных членов.
-
столбец свободных членов.
Тогда исходную СЛАУ
можно переписать в виде:
![]() (3`).
(3`).
Методы решения СЛАУ делятся на две группы:
прямые;
итерационные.
Прямые методы решения
СЛАУ – это методы, позволяющие отыскать
решение системы при помощи конечного
числа арифметических действий. Если
при этом исходные данные задачи (матрица
и вектор
![]() )
заданы точно и все арифметические
операции выполнены точно, то прямые
методы позволяют получить точное решение
СЛАУ. Однако на практике решение чаще
всего получается приближённое.
)
заданы точно и все арифметические
операции выполнены точно, то прямые
методы позволяют получить точное решение
СЛАУ. Однако на практике решение чаще
всего получается приближённое.
К таким методам относится: метод Крамера, метод обратной матрицы, метод Гаусса и др.
Итерационные методы основаны на построении последовательности приближений, при определённых условиях сходящиеся к точному решению СЛАУ.
К таким методам относится: метод простой итерации, метод Зейделя и др.
{ Самостоятельно законспектировать тему: «Сравнение прямых и итерационных методов»}
Метод Гаусса – прямой метод решения СЛАУ
Метод основан на последовательном исключении неизвестных, благодаря чему исходная система приводится к треугольному или трапециевидному виду.
{ Самостоятельно законспектировать тему: «Метод Гаусса решения СЛАУ»}
Метод квадратного корня – прямой метод решения СЛАУ
Пусть задана СЛАУ:
(1)
с вещественной симметричной матрицей
![]() .
.
Предположим, что все
главные миноры матрицы
отличны от нуля. В этом случае матрицу
можно разложить в произведение двух
треугольных матриц:
![]() ,
где
- верхняя треугольная матрица
,
где
- верхняя треугольная матрица
 .
.
Потребуем, чтоб все
элементы на главной диагонали матрицы
были одного знака (для определённости
![]() ).
С этой целью мы выполняем умножение
).
С этой целью мы выполняем умножение
![]() .
Приравниваем элементы полученного
произведения соответствующим элементам
матрицы
.
.
Приравниваем элементы полученного
произведения соответствующим элементам
матрицы
.
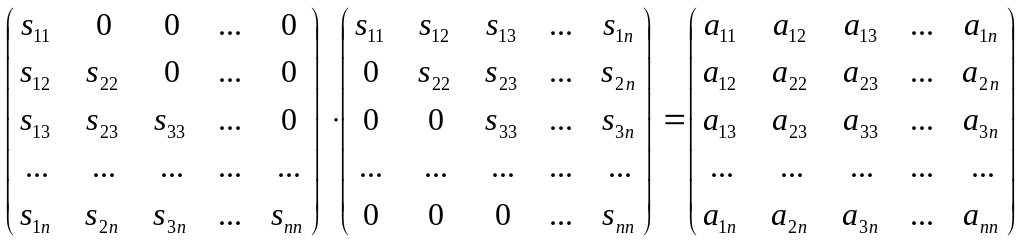
Так как матрица симметричная, то полученные равенства достаточно рассмотреть лишь для элементов, стоящих выше главной диагонали.
Шаг 1.
Умножим первую строку матрицы
![]() на все столбцы матрицы
и приравняем соответствующим элементам
матрицы
,
получим:
на все столбцы матрицы
и приравняем соответствующим элементам
матрицы
,
получим:
![]() ,
,
![]() ,
,
![]() ,…,
,…,![]() .
Отсюда получим:
.
Отсюда получим:
![]() ,
,
![]() (2).
(2).
Шаг 2.
Умножим вторую строку матрицы
на все столбцы матрицы
начиная со второго и приравняем
соответствующим элементам матрицы
,
получим:
![]() ,
,
![]() .
Отсюда получим:
.
Отсюда получим:
![]() ,
,
![]() .
.
и т.д. запишем формулы
для нахождения элементов произвольной
![]() -й
строки матрицы
.
-й
строки матрицы
.
Шаг i.
(![]() )
Умножим
-ю
строку матрицы
на все столбцы матрицы
начиная с
-го
и приравняем соответствующим элементам
матрицы
,
получим:
)
Умножим
-ю
строку матрицы
на все столбцы матрицы
начиная с
-го
и приравняем соответствующим элементам
матрицы
,
получим:
![]() ,
,
![]() .
Отсюда получим:
.
Отсюда получим:
![]() ,
,
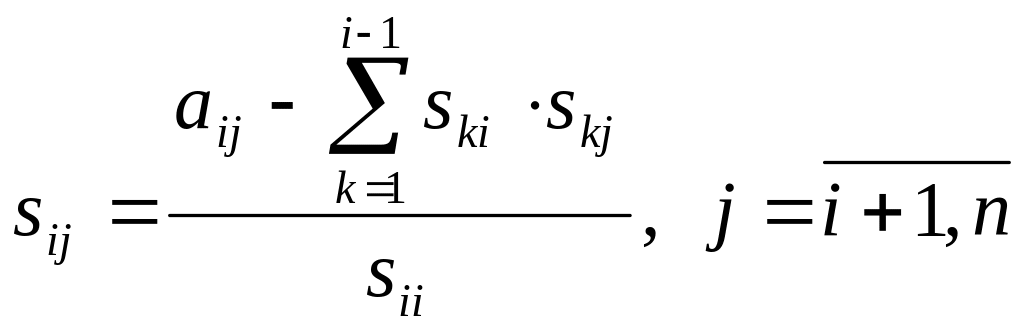 (3).
(3).
Таким образом, после
шагов, выполненных по данной схеме, мы
найдём все элементы матрицы
.
Тогда исходную систему уравнений
можно переписать в виде:
![]() .
Введём обозначения
.
Введём обозначения
![]() ,
где
,
где
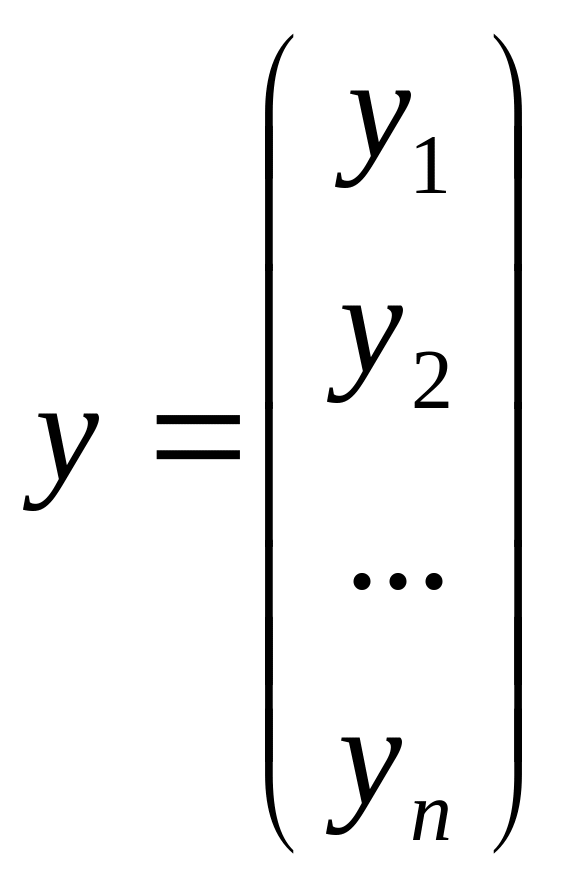 -
пока неизвестный вектор. Тогда исходная
система уравнений (1)
приводится к следующему виду:
-
пока неизвестный вектор. Тогда исходная
система уравнений (1)
приводится к следующему виду:
![]() .
То есть исходная система свелась к
решению двух систем треугольного вида.
Распишем систему уравнений (4)
в координатной форме:
.
То есть исходная система свелась к
решению двух систем треугольного вида.
Распишем систему уравнений (4)
в координатной форме:
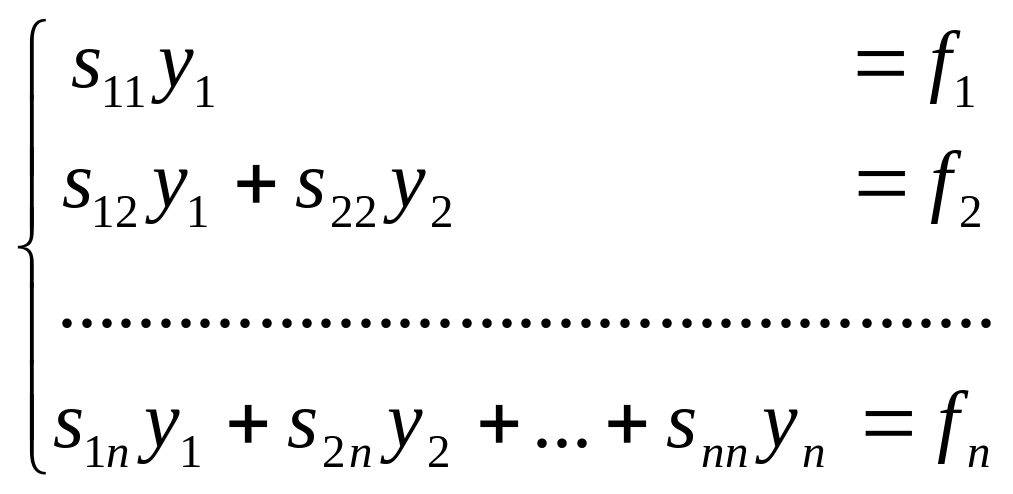 (4`).
(4`).
Отсюда получим следующие
формулы для нахождения вектора
:
![]() ,
,
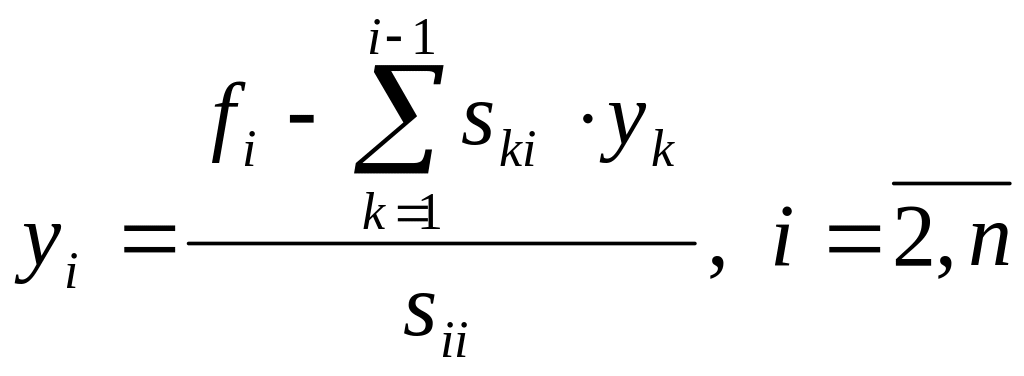 (6).
(6).
Распишем систему
уравнений (5)
в координатной форме:
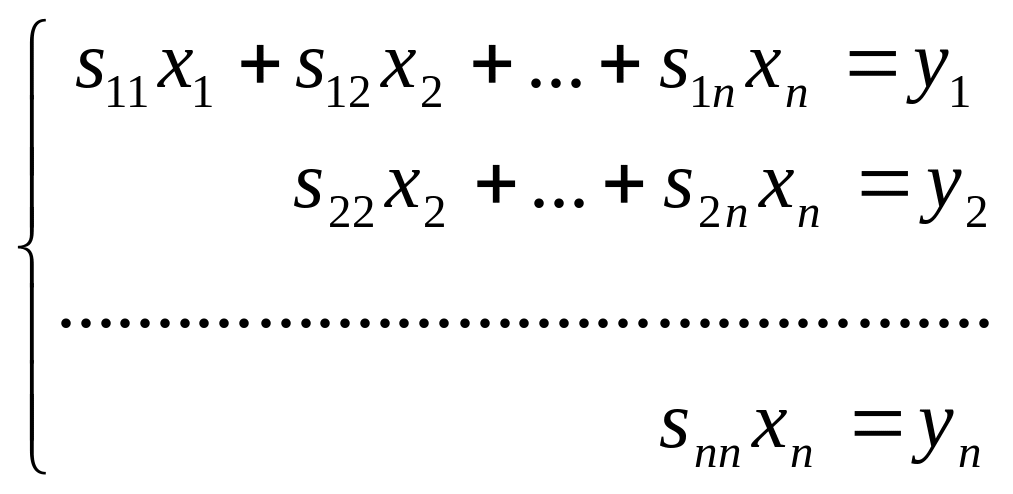 (5`).
(5`).
Отсюда получим следующие
формулы для нахождения вектора
:
![]() ,
,
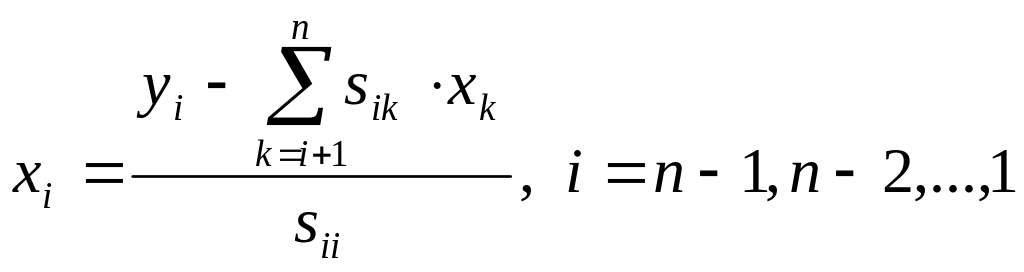 (7).
(7).
Формулы (7)
определяют искомое решение
![]() системы (1).
системы (1).
Замечание.
Элементы матрицы
:![]() ,
которые вычисляются по формулам (2),
(3) будут
вещественными, если исходная матрица
является положительно определённой.
,
которые вычисляются по формулам (2),
(3) будут
вещественными, если исходная матрица
является положительно определённой.
Определение.
Симметричная, квадратная матрица
называется положительно определённой,
если для
![]() .
Согласно критерия Сильвестра для
положительной определённости симметричной
матрицы
необходимо и достаточно чтоб все её
главные миноры были >0.
.
Согласно критерия Сильвестра для
положительной определённости симметричной
матрицы
необходимо и достаточно чтоб все её
главные миноры были >0.
Из формул (2)
и (3)
видно, что
-вещественное
число, если
![]() ;
;
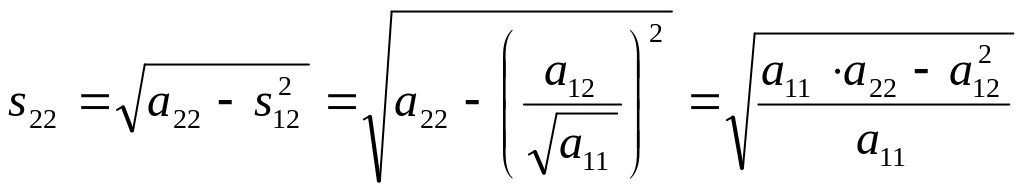 -вещественное
число, если
-вещественное
число, если
![]() и т.д.
и т.д.
Из формул для нахождения видно, что если хотя бы один из главных миноров матрицы равен нулю, то разложение матрицы в произведение невозможно, поскольку в формулах (2), (3), (6) и (7) появляется деление на ноль. Метод квадратного корня в таком случае не применим.
Метод ортогонализации – прямой метод решения СЛАУ
Пусть задана
последовательность векторов
![]() .
.
Последовательность
векторов
![]() называется ортогональной, если
называется ортогональной, если
![]() .
Последовательность векторов
называется ортонормированной, если она
ортогональна в
.
Последовательность векторов
называется ортонормированной, если она
ортогональна в
![]() и Эвклидова норма каждого вектора
и Эвклидова норма каждого вектора
![]() .
.
Другими словами
последовательность векторов
ортонормированна, если
![]() .
.
Утверждение. По любой линейно независимой системе векторов можно построить ортонормированную систему.
Пусть задана СЛАУ: (1) с невырожденной матрицей ( - существует единственное решение).
Введём следующие
обозначения: для каждой
-й
строки обозначим через
![]() следующий вектор
следующий вектор
![]() и через
и через
![]() вектор размерности
,
такой что
вектор размерности
,
такой что
![]() .
Тогда исходная СЛАУ (1)
перепишется в виде:
.
Тогда исходная СЛАУ (1)
перепишется в виде:
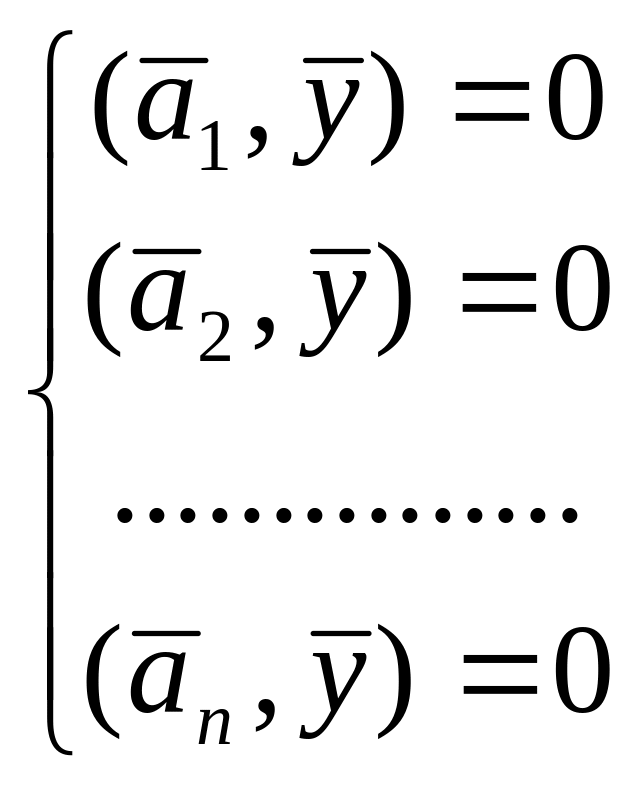 (1`).
(1`).
Таким образом, задача
решения СЛАУ (1)
сводится к нахождению вектора
ортогонального всем линейно независимым
векторам
![]() и последняя координата которого равна
1.
и последняя координата которого равна
1.
Такой вектор будет единственным в силу единственности решения СЛАУ (1).
введём в рассмотрение
ещё один вспомогательный вектор
![]() и покажем, что последовательность
векторов
и покажем, что последовательность
векторов
![]() является линейно независимыми, то есть
является линейно независимыми, то есть
![]() (2),
только тогда, когда
(2),
только тогда, когда
![]() .
Запишем (2)
в развёрнутой покоординатной форме:
.
Запишем (2)
в развёрнутой покоординатной форме:
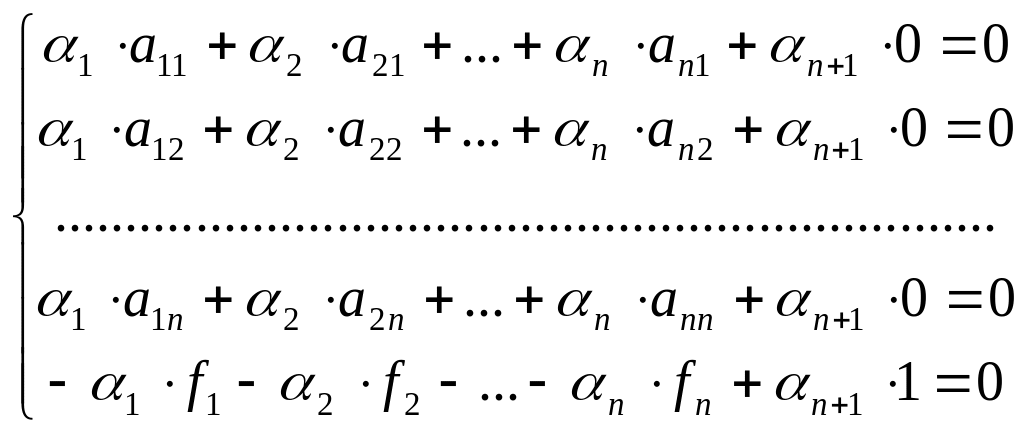 (2`).
(2`).
(2`)
представляет собой однородную СЛАУ
относительно коэффициентов
![]() .
Определитель системы имеет вид:
.
Определитель системы имеет вид:
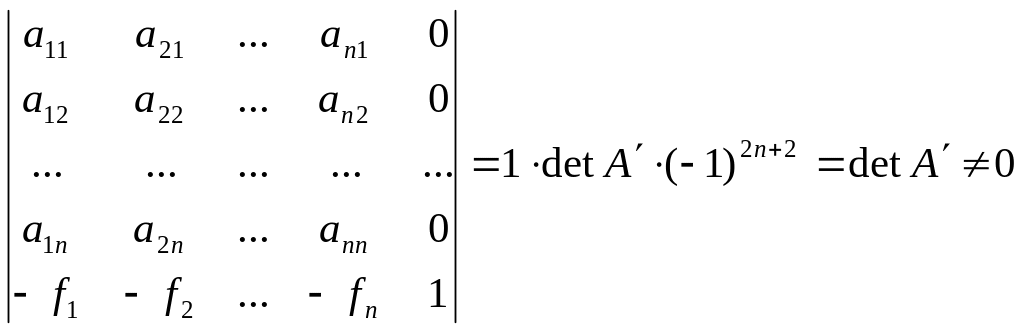 .
.
Так как
![]() ,
то однородная СЛАУ (2`)
имеет единственное тривиальное решение:
.
,
то однородная СЛАУ (2`)
имеет единственное тривиальное решение:
.
Таким образом, система
векторов
-
линейно независимая в пространстве
![]() .
.
Подвергнем систему
векторов
процессу ортогонализации Шмидта в
Эвклидовой метрике. То есть построим
на основе этих векторов ортонормированную
систему векторов
![]() .
.
Шаг 1.
Введём вспомогательный вектор
![]() ,
тогда
,
тогда
![]() ,
,
 .
.
Шаг 2.
![]() ,
где
,
где
![]() ,
которую подбираем так, чтоб выполнялось
условие
,
которую подбираем так, чтоб выполнялось
условие
![]() :
:
![]() .
Очевидно, что
.
Очевидно, что
![]() так как является линейной комбинацией
линейно независимых векторов
так как является линейной комбинацией
линейно независимых векторов
![]() и
и
![]() с по крайней мере одним коэффициентом
не равным нулю при
,
тогда
с по крайней мере одним коэффициентом
не равным нулю при
,
тогда
![]() .
Ясно, что
.
Ясно, что
![]() и
и
![]() и т.д.
и т.д.
Предположим, что векторы
![]() уже построены с такими свойствами, что
уже построены с такими свойствами, что
![]() .
Рассмотрим
-й
шаг:
.
Рассмотрим
-й
шаг:
Шаг к.
(![]() )
Определим вспомогательный вектор
)
Определим вспомогательный вектор
![]() (3),
(3),
где
![]() .
Рассмотрим
.
Рассмотрим

![]() .
.
![]() так как является
линейной комбинацией линейно независимых
векторов
так как является
линейной комбинацией линейно независимых
векторов
![]() .
Тогда
.
Тогда
![]() .
.
Таким образом, в
результате выполнения
шагов процесса ортогонализации Шмидта
ортонормированная последовательность
векторов
![]() будет построена. Покажем, что последний
вектор
будет построена. Покажем, что последний
вектор
![]() этой последовательности ортогонален
всем линейно независимым векторам
.
Для этого для
этой последовательности ортогонален
всем линейно независимым векторам
.
Для этого для
![]() из формулы (3):
рассмотрим скалярное произведение
из формулы (3):
рассмотрим скалярное произведение
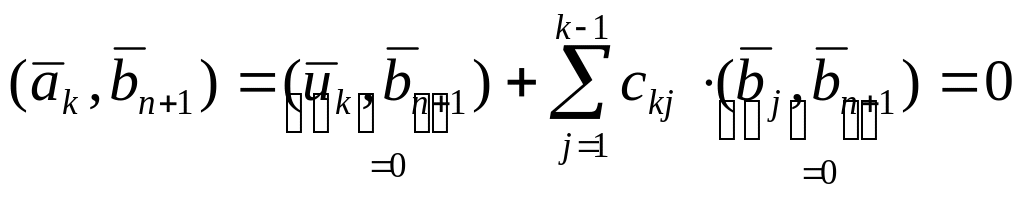 .
Таким образом, вектор
ортогонален всем векторам
.
Таким образом, вектор
ортогонален всем векторам
![]() .
Покажем что последняя координата вектора
не равна нулю:
.
Покажем что последняя координата вектора
не равна нулю:
![]() .
Надо показать, что
.
Надо показать, что
![]() .
Предположим иное, пусть
.
Предположим иное, пусть
![]() .
Рассмотрим равенство:
.
Рассмотрим равенство:
![]() ,
,![]() .
Распишем его в координатной форме:
.
Распишем его в координатной форме:
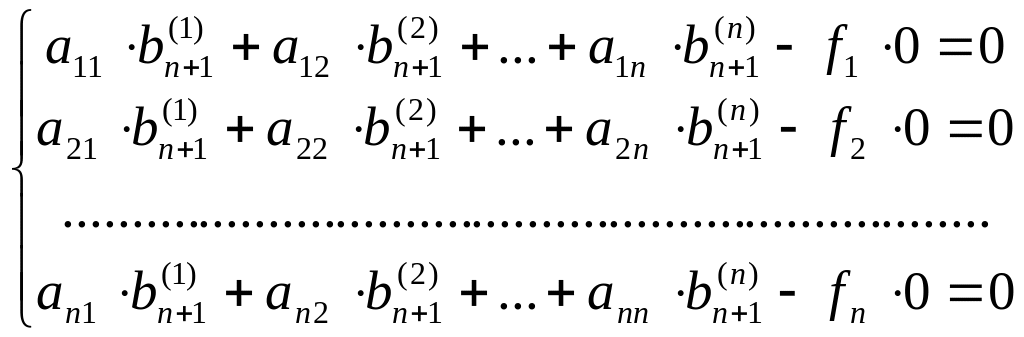 .
.
Получим однородную
СЛАУ относительно первых
координат вектора
,
определитель этой системы совпадает с
определителем матрицы
:
.
Следовательно, данная система имеет
единственное тривиальное решение
![]() ,
то есть
,
то есть
![]() ,
что невозможно по построению. Тогда
и в качестве вектора
возьмём
,
что невозможно по построению. Тогда
и в качестве вектора
возьмём
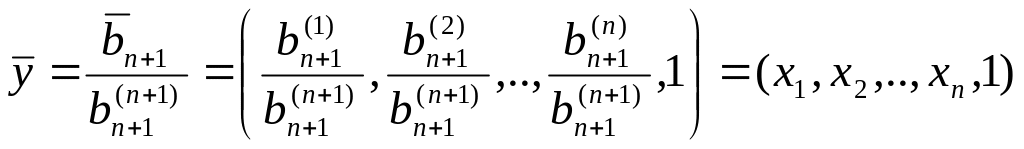 .
Таким образом, вектор
построен.
.
Таким образом, вектор
построен.
Метод простой итерации (МПИ) – итерационный метод решения СЛАУ
Пусть задана СЛАУ: (1) с невырожденной матрицей ( - существует единственное решение).
Пусть вектор
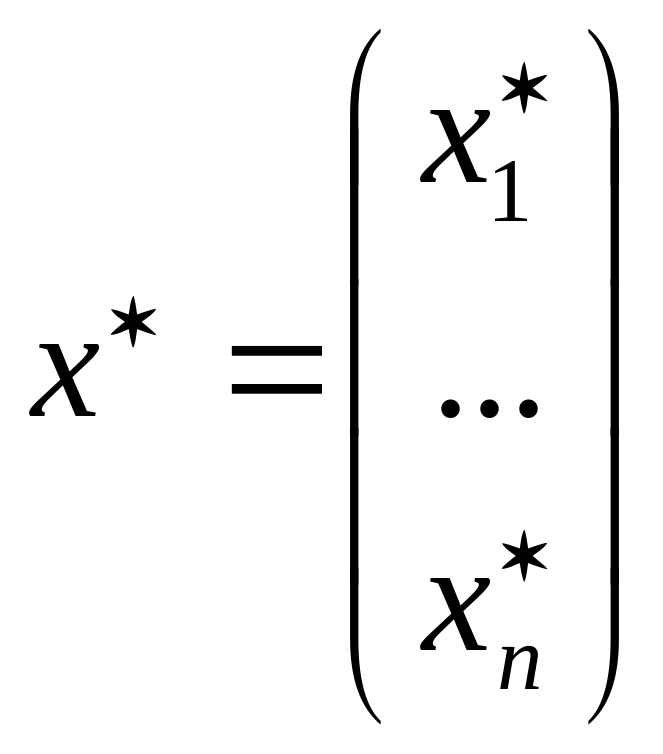 -
вектор столбец точного решения,
-
вектор столбец точного решения,
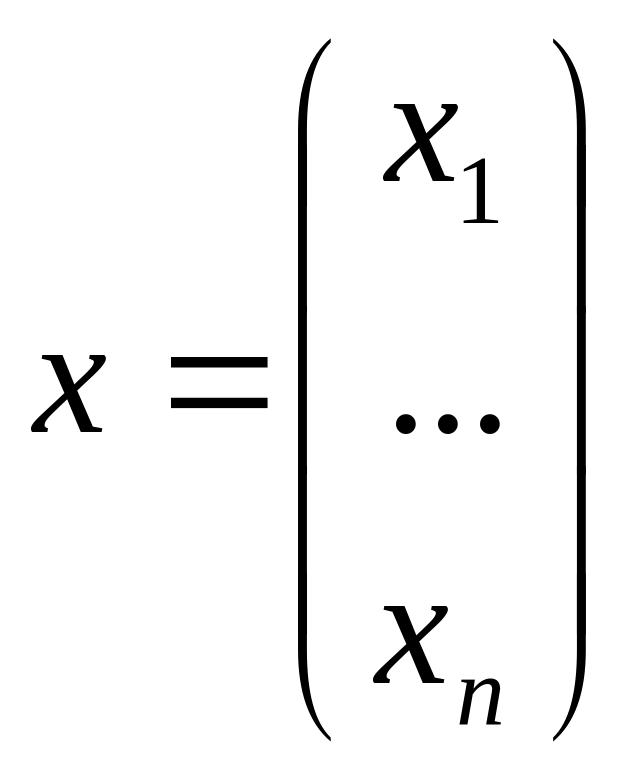 -
вектор столбец неизвестных,
-
вектор столбец неизвестных,
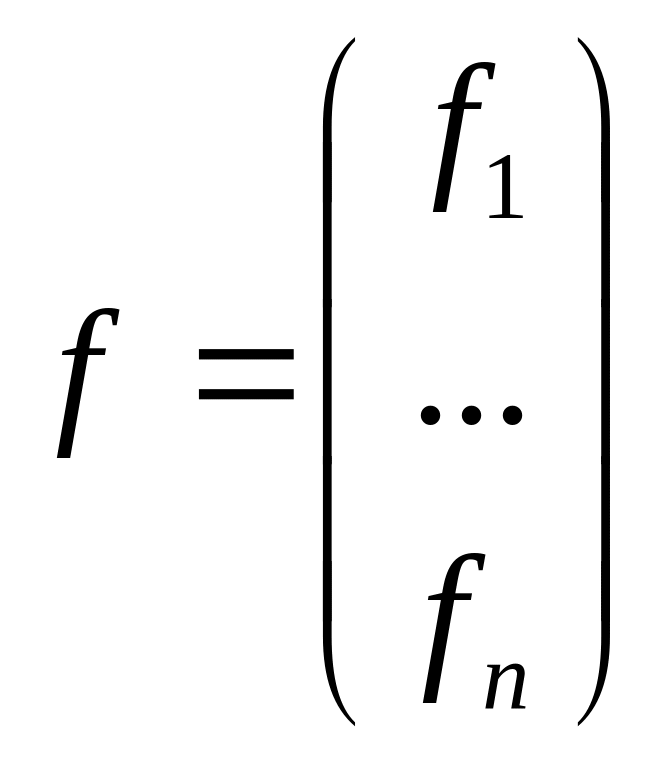 -
вектор столбец свободных членов СЛАУ
(1).
-
вектор столбец свободных членов СЛАУ
(1).
Каким-либо способом
(будут указаны ниже) приведём систему
(1)
к эквивалентному виду удобному для
итерирования:
![]() (2),
где
квадратная матрица,
(2),
где
квадратная матрица,
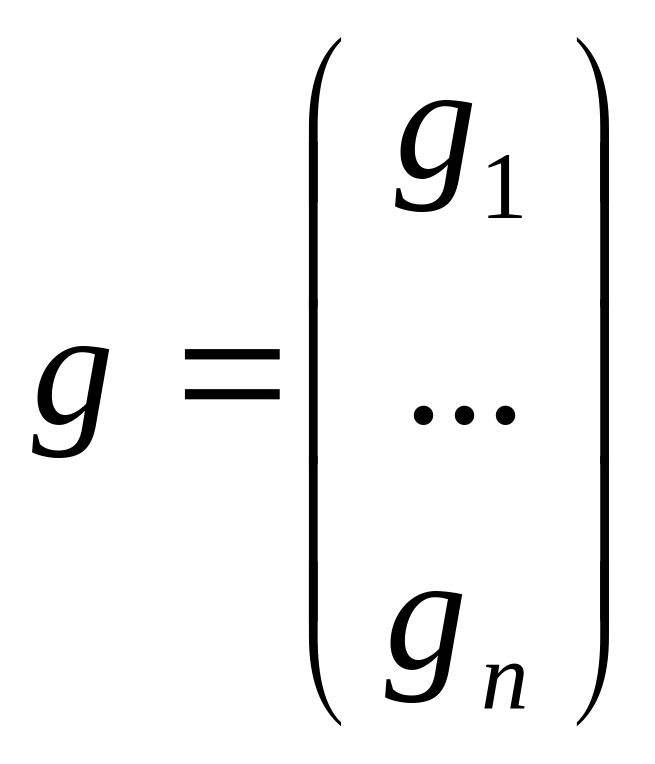 -
вектор столбец свободных членов.
-
вектор столбец свободных членов.
Выберем некоторое
начальное приближение
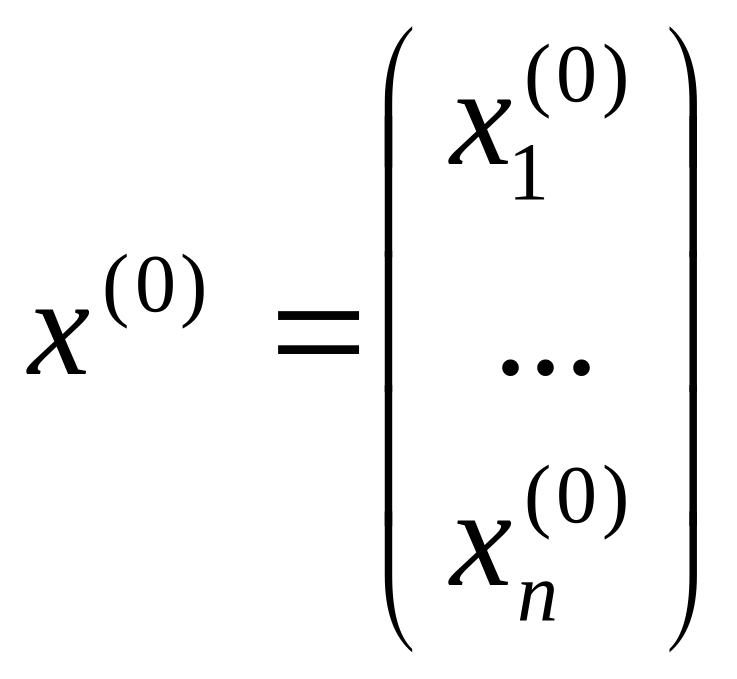 исходя из которого построим приближение
по формуле:
исходя из которого построим приближение
по формуле:
![]() .
Исходя из
.
Исходя из
![]() построим приближение
по формуле:
построим приближение
по формуле:![]() .
.
Если
уже построено, то мы можем построить
приближение по формуле:
![]() ,
,
![]() (3)
– формула МПИ
для решения СЛАУ (1)
(или что то же самое СЛАУ (2)).
(3)
– формула МПИ
для решения СЛАУ (1)
(или что то же самое СЛАУ (2)).
В координатной форме МПИ записывается следующим образом:
![]() (3`).
(3`).
Говорят, что МПИ для
СЛАУ (1)
сходится, если предел последовательности
приближений, определяемый формулой (3)
существует и равен
![]() :
:
![]() .
.
При этом вектор
![]() называется погрешность итерационного
метода на
-й
итерации, а вектор
называется погрешность итерационного
метода на
-й
итерации, а вектор
![]() называется невязкой итерационного
метода на
-й
итерации.
называется невязкой итерационного
метода на
-й
итерации.
Выясним условие сходимости МПИ.
Теорема 1.
Для того чтобы МПИ для СЛАУ (1)
сходился независимо от выбора начального
приближения
необходимо и достаточно, чтоб все
собственные значения матрицы
были по модулю меньше 1. То есть, чтоб
все корни характеристического уравнения
![]() .
.
Лемма 1.
Модуль каждого собственного значения
матрицы не превосходит любой из её норм:
![]() .
.
Проверка условий
теоремы 1 на практике затруднительна,
так как связана с нахождением собственных
значений матрицы
![]() ,
поэтому часто пользуются следующим
условием сходимости (достаточное
условие).
,
поэтому часто пользуются следующим
условием сходимости (достаточное
условие).
Теорема 2.
Для того чтобы МПИ для СЛАУ (1)
сходился независимо от выбора начального
приближения
достаточно, чтоб какая-либо норма матрицы
была меньше 1:
![]() .
.
Но с другой стороны условие теоремы 2 является более жёстким по сравнению с условием теоремы 1, поскольку в силу леммы 1 нарушение условия теоремы 2 ещё не означает, что метод расходится.
Теорема 3 (об оценке
погрешности).
Если какая-либо норма матрицы
(
)
согласована с данной нормой вектора,
то справедлива следующая оценка
погрешности МПИ:
![]() (4).
(4).
Замечание 1.
Из доказательства теоремы 3 можно легко
получить следующее неравенство:
![]() .
.
Следовательно МПИ
обладает линейной скоростью сходимости
или скоростью сходимости геометрической
прогрессии со знаменателем
![]() ,
.
Чем меньше
,
тем выше фактическая скорость сходимости
метода.
,
.
Чем меньше
,
тем выше фактическая скорость сходимости
метода.
Замечание 2. МПИ, как следует из теорем 1-2, сходится независимо от выбора начального приближения . Однако, если выбрано неудачно это может привести к большому количеству итераций. Из произвола в выборе следует важное свойство МПИ – самоисправляемость: отдельные ошибки в вычислениях (погрешность округления) не влияют на факт сходимости, поскольку ошибочное приближение может рассматриваться как новое начальное.
Выясним критерий
окончания итерационного процесса. Для
получения приближенного решения исходной
СЛАУ с точностью
![]() ,
естественно в качестве критерия окончания
выбрать тот, который вытекает из формулы
(4):
,
естественно в качестве критерия окончания
выбрать тот, который вытекает из формулы
(4):
![]() (5)
– близкий к истинному критерий окончания.
(5)
– близкий к истинному критерий окончания.
Можно пользоваться
также ложными критериями (их выполнение
не гарантирует, что
![]() ):
):
![]() (6)
или
(6)
или![]() (7).
(7).
Отметим, что если
![]() ,
то тогда критерий (6)
совпадает с критерием (5),
то есть становиться близким к истинному.
,
то тогда критерий (6)
совпадает с критерием (5),
то есть становиться близким к истинному.
Рассмотрим способы приведения СЛАУ (1) к виду удобному для итерирования.
Способ 1.
Пусть матрица
положительно определённая, тогда все
её собственные значения
![]() .
Рассмотрим исходную систему
и выполним следующие эквивалентные
преобразования: умножим обе части на
,
получим
.
Рассмотрим исходную систему
и выполним следующие эквивалентные
преобразования: умножим обе части на
,
получим
![]() .
Далее перенесём все в правую часть
.
Далее перенесём все в правую часть
![]() ,
,
![]() ,
,
![]() .
.
Таким образом, полученная
система уравнений имеет вид (2),
где в качестве матрицы
выступает матрица
![]() ,
а в качестве вектора
,
а в качестве вектора
![]() свободных членов – вектор
свободных членов – вектор
![]() .
.
МПИ в этом случае
записывается в виде:
![]() ,
,
![]() (8).
(8).
Значение константы
выберем так, чтоб МПИ (8)
был сходящимся. Воспользуемся необходимым
и достаточным условием МПИ: собственное
значение
![]() ,
тогда
,
тогда
![]() .
Решение этого модульного неравенства
имеет вид:
.
Решение этого модульного неравенства
имеет вид:
![]() ,
где
,
где
![]() - наибольшее собственное значение
матрицы
.
Заметим, что МПИ (8)
будет сходиться быстрее всего при
следующем оптимальном значении параметра
- наибольшее собственное значение
матрицы
.
Заметим, что МПИ (8)
будет сходиться быстрее всего при
следующем оптимальном значении параметра
![]() ,
где
,
где
![]() и
и
![]() соответственно наибольшее и наименьшее
собственные значения матрицы
.
соответственно наибольшее и наименьшее
собственные значения матрицы
.
Поскольку собственные
значения матрицы
бывают неизвестны, то с учётом леммы
1![]() :
:
![]() .
.
Замечание.
Если исходная матрица
не является положительно определённой,
тогда исходную систему уравнений
домножим слева на матрицу![]() -
транспонированная комплексно сопряжённая
к матрице
.
Тогда получим
-
транспонированная комплексно сопряжённая
к матрице
.
Тогда получим
![]() (9) –
эквивалентна СЛАУ (1),
где матрица
(9) –
эквивалентна СЛАУ (1),
где матрица
![]() является положительно определённой.
Затем к полученной системе (9)
применяют
описанный выше способ сведения к виду
удобному для итерирования.
является положительно определённой.
Затем к полученной системе (9)
применяют
описанный выше способ сведения к виду
удобному для итерирования.
Способ 2.
Пусть матрица
такая, что диагональные элементы в ней
доминируют по строкам или по столбцам.
Это означает, что
![]() (10) –
доминирование по строкам или
(10) –
доминирование по строкам или
![]() (11) –
доминирование по столбцам.
(11) –
доминирование по столбцам.
Лемма 1. Если в матрице имеет место диагональное преобладание по строкам или по столбцам, то определитель такой матрицы отличен от нуля, то есть матрица невырождена.
Из диагонального
преобладания следует, что
![]() .
Разрешим каждое из уравнений системы
(1)
относительно диагонального неизвестного:
.
Разрешим каждое из уравнений системы
(1)
относительно диагонального неизвестного:
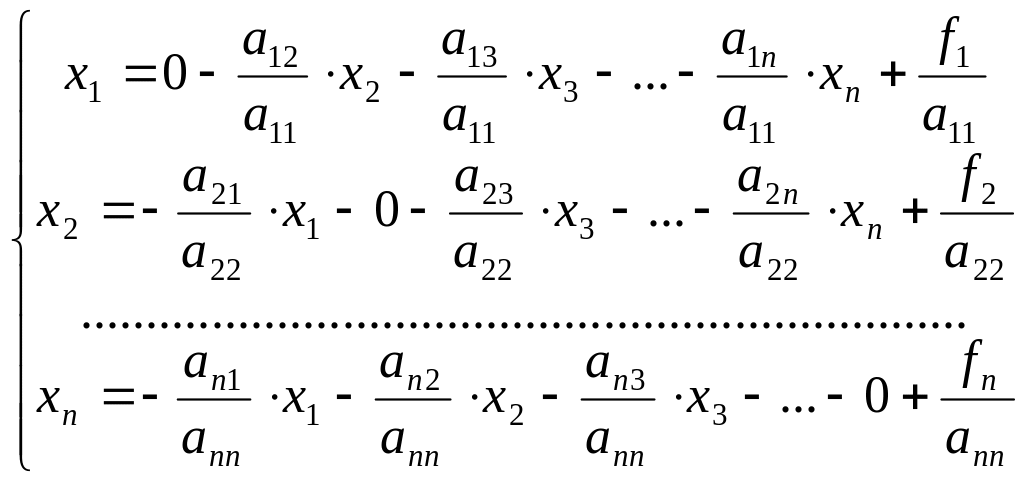 (12),
где
(12),
где
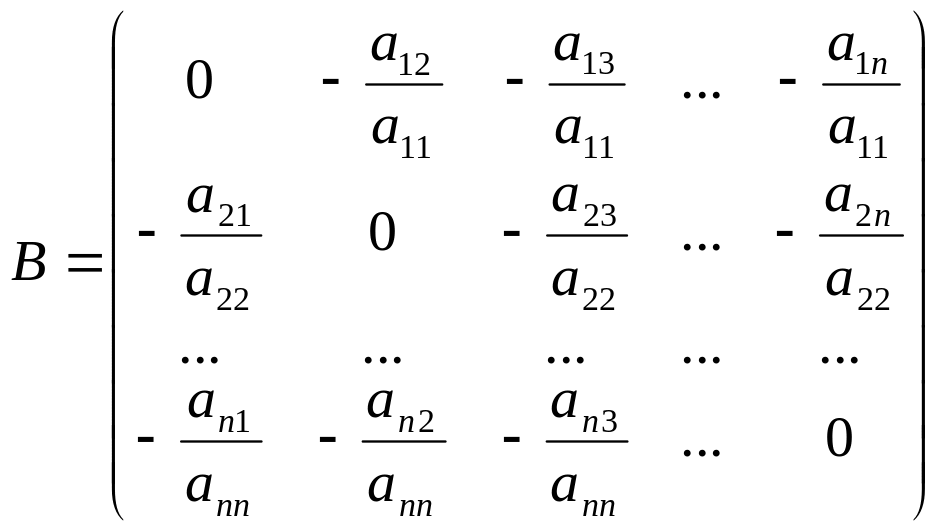 и
и
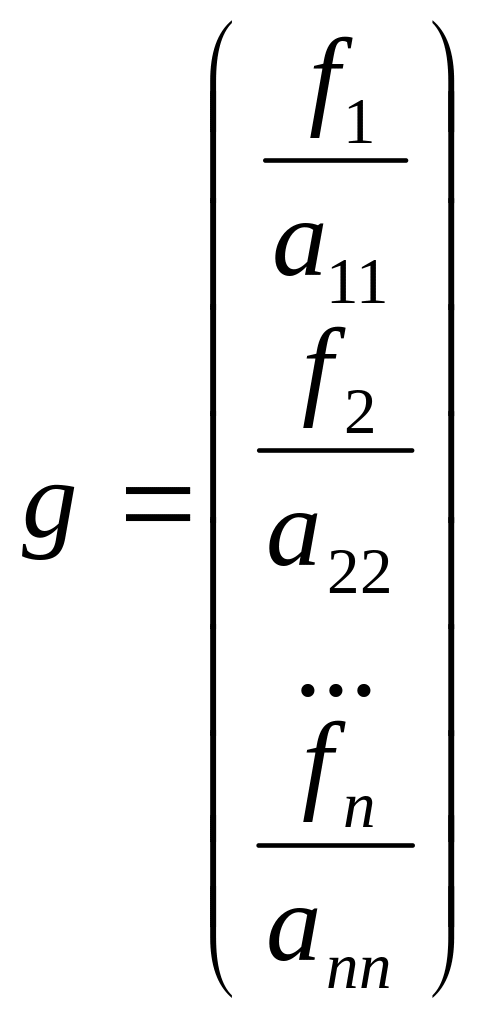 .
.
Таким образом, система (1) свелась к эквивалентной системе вида (2).
МПИ для решения системы (12) с учётом формулы (3`) имеет вид:
![]() (13)
– метод Якоби.
(13)
– метод Якоби.
Выясним условия
сходимости метода Якоби. Предположим
для определённости, что в матрице
диагональные элементы доминируют по
строкам (выполняется условие (10)).
Рассмотрим
![]() .
Мы получили, что по теореме 2 выполняется
достаточное условие сходимости. Таким
образом, метод Якоби сходится.
.
Мы получили, что по теореме 2 выполняется
достаточное условие сходимости. Таким
образом, метод Якоби сходится.
Аналогично, можно
показать, что если выполняется условие
(11),
то
![]() и метод Якоби также сходится.
и метод Якоби также сходится.
Замечание. Во многих практических ситуациях произвольную систему с невырожденной матрицей удаётся привести к системе с диагональным преобладанием по строкам или по столбцам с помощью эквивалентных преобразований над уравнениями системы.
Метод Зейделя – итерационный метод решения СЛАУ
Пусть задана СЛАУ: (1) с невырожденной матрицей ( - существует единственное решение) и - вектор столбцом свободных членов.
Так же как и раньше приведём систему (1) к виду удобному для итерирования (2), где - квадратная матрица, - вектор столбец неизвестных, - вектор столбец свободных членов.
Пусть вектор - вектор столбец точного решения СЛАУ (1) (или что то же самое СЛАУ (2)).
Напомним формулу МПИ для решения системы (2): , (3). Распишем эту итерационную формулу покоординатно:
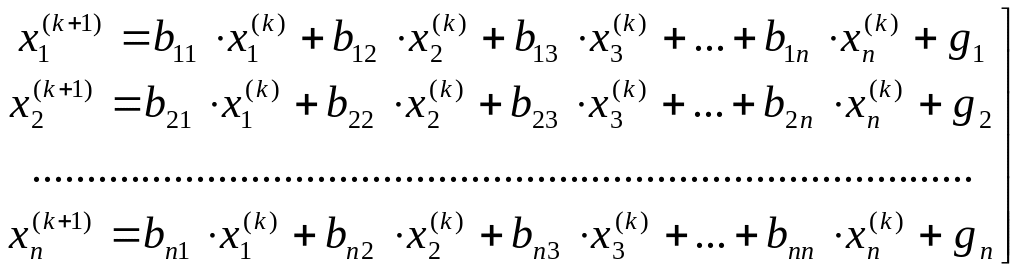 (3`).
(3`).
Метод Зейделя, применяемый
к системе уравнений (2),
представляет собой модификацию МПИ,
которая состоит в том, что при вычислении
каждой новой координаты
![]() -
го приближения используются уже
вычисленные ранее координаты этого
-
го приближения, то есть в координатной
форме метод Зейделя имеет вид:
-
го приближения используются уже
вычисленные ранее координаты этого
-
го приближения, то есть в координатной
форме метод Зейделя имеет вид:
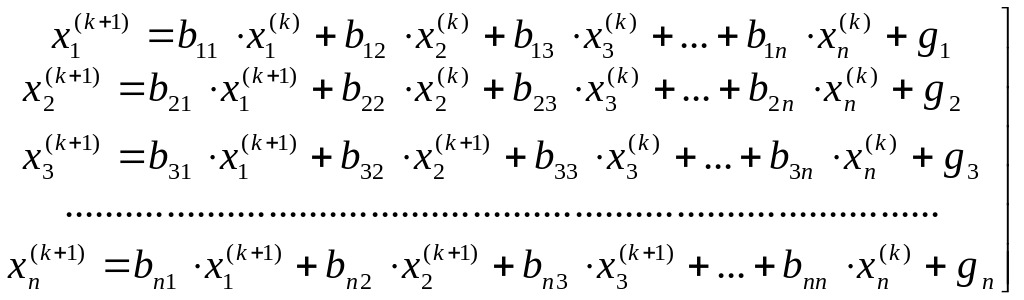 (4).
(4).
Перепишем (4)
в компактной матричной форме, для этого
представим матрицу
в виде суммы двух треугольных матриц:
![]() ,
где
,
где
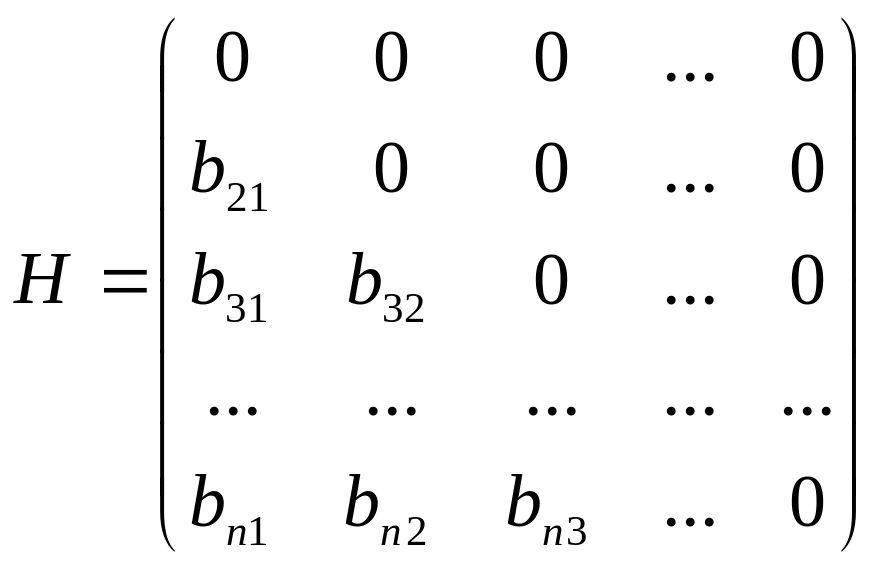 и
и
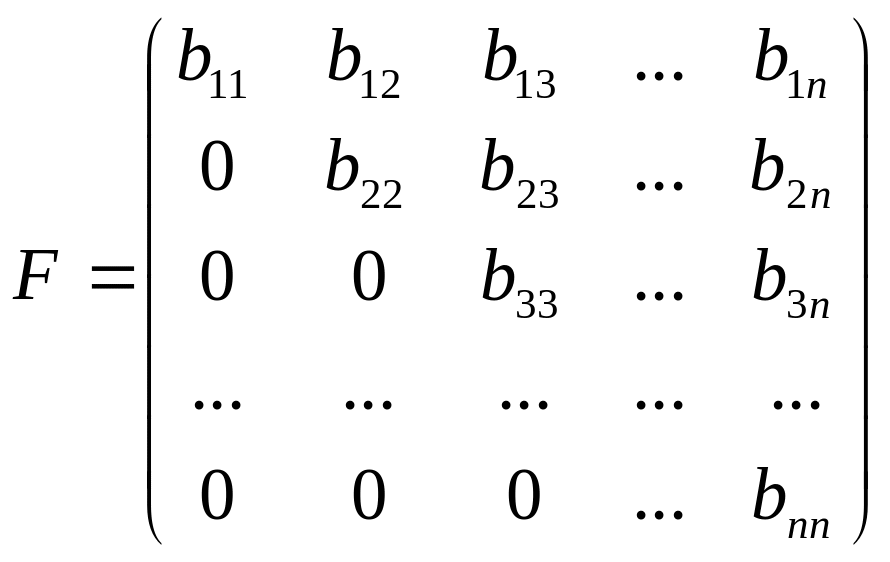 ,
,
тогда формулы (4) можно записать в следующем виде:
![]() (4`)
или
(4`)
или
![]() .
.
Рассмотрим матрицу
![]() -
нижняя треугольная матрица с единицами
на главной диагонали:
-
нижняя треугольная матрица с единицами
на главной диагонали:
![]() следовательно, существует обратная ей
матрица. Тогда
следовательно, существует обратная ей
матрица. Тогда
![]() (5),
так как
(5),
так как
![]() .
Формула (5)
представляет собой метод Зейделя для
СЛАУ (2).
С другой стороны, формула (5)
является формулой МПИ для СЛАУ следующего
вида:
.
Формула (5)
представляет собой метод Зейделя для
СЛАУ (2).
С другой стороны, формула (5)
является формулой МПИ для СЛАУ следующего
вида:
![]() (6).
И тогда условие сходимости метода
Зейделя можно формулировать на основе
условий сходимости МПИ.
(6).
И тогда условие сходимости метода
Зейделя можно формулировать на основе
условий сходимости МПИ.
Замечание. Итерационная формула (5) используется, как правило, для выяснения условий сходимости, то есть имеет теоретическое значение. На практике она не применяется, так как связана с обращением матрицы.
Теорема 1.
Для того чтобы метод Зейделя для СЛАУ
(2)
сходился независимо от выбора начального
приближения
необходимо и достаточно, чтоб все
собственные значения матрицы
![]() были по модулю меньше 1. Другими словами,
чтоб все корни
были по модулю меньше 1. Другими словами,
чтоб все корни
![]() характеристического уравнения
характеристического уравнения
![]() (7).
(7).
Теорема 2.
Для того чтобы метод Зейделя для СЛАУ
(2)
сходился независимо от выбора начального
приближения
необходимо и достаточно, чтоб все корни
характеристического уравнения
![]() (8)
по модулю были меньше 1.
(8)
по модулю были меньше 1.
Доказательство.
Покажем, что уравнения (7)
и (8)
имеют одинаковые корни:

Определители в левой
и правой части обращаются в ноль
одновременно при одинаковых значениях
![]() ,
то есть уравнения (7)
и (8)
имеют одинаковые корни.
,
то есть уравнения (7)
и (8)
имеют одинаковые корни.
Замечание 1.
Проверка условий теоремы 2 , очевидно
гораздо проще на практике, чем условий
теоремы 1, так как не требует обращения
матрицы
![]() .
.
Замечание 2.
Условие сходимости (необходимое и
достаточное) МПИ для системы уравнений
(2)
имеют вид:
(9),
где
![]() .
Сравнивая это условие с условием теоремы
2 мы видим, что уравнения (8)
и (9)
имеют различные корни. Отсюда следует,
что метод Зейделя и МПИ для СЛАУ (2)
имеют разные области сходимости. То
есть существует система уравнений, для
которой один из методов сходится, а
другой расходится.
.
Сравнивая это условие с условием теоремы
2 мы видим, что уравнения (8)
и (9)
имеют различные корни. Отсюда следует,
что метод Зейделя и МПИ для СЛАУ (2)
имеют разные области сходимости. То
есть существует система уравнений, для
которой один из методов сходится, а
другой расходится.
Теорема 3.
Для того чтобы метод Зейделя для СЛАУ
(2)
сходился независимо от выбора начального
приближения
достаточно, чтоб какая-либо норма
![]() .
.
Теорема 4. Для того чтобы метод Зейделя для СЛАУ (2) сходился независимо от выбора начального приближения достаточно, чтоб выполнялось одно из двух условий:
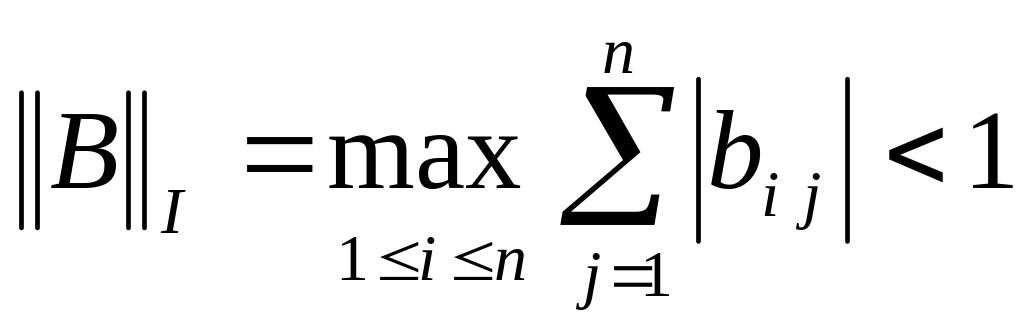 ;
; .
.
Теорема 5.
Пусть выполняется условие теоремы 4,
тогда для метода Зейделя справедлива
следующая оценка погрешности:
![]() (10),
где
(10),
где
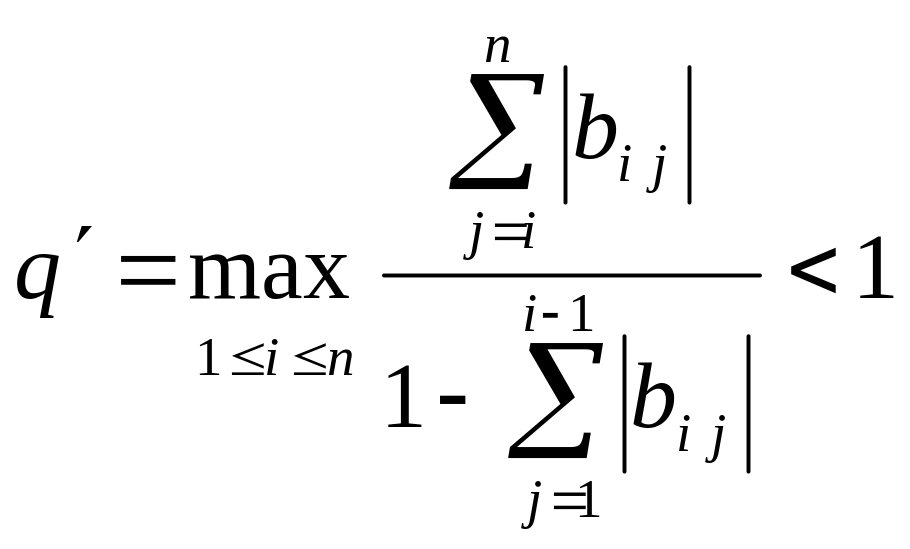 .
Из доказательства теоремы 5 вытекает,
что метод Зейделя обладает линейной
скоростью сходимости или скоростью
сходимости геометрической прогрессии
со знаменателем
.
Из доказательства теоремы 5 вытекает,
что метод Зейделя обладает линейной
скоростью сходимости или скоростью
сходимости геометрической прогрессии
со знаменателем
![]() ,
причём легко показать, что
,
причём легко показать, что
![]() .
Таким образом, метод Зейделя сходится
не медленнее МПИ, в том случае, когда
оба метода сходятся.
.
Таким образом, метод Зейделя сходится
не медленнее МПИ, в том случае, когда
оба метода сходятся.
Рассмотрим один из способов приведения СЛАУ (1) к виду удобному для итерирования.
Предположим, что в исходной матрице ( ) имеет место диагональное преобладание по строкам или по столбцам: .
Разрешим каждое из уравнений системы (1) относительно диагонального неизвестного в результате этого система принимает вид:
![]() (11)
– система вида (2).
(11)
– система вида (2).
Применение метода Зейделя к системе уравнений (11) даёт нам следующие расчётные формулы:
![]() (12)
– метод Некрасова для решения СЛАУ (1).
(12)
– метод Некрасова для решения СЛАУ (1).
Если выполняется условие теоремы 4, то метод Некрасова будет сходиться.
