Квадратурные формулы наивысшей алгебраической степени точности (н.А.С.Т.)

Ранее было получено, что интерполяционные квадратурные формулы построенные по узлам имеют алгебраическую степень точности по меньшей мере . Возникает вопрос существуют ли более точные квадратурные формулы более высокой степени точности и какова наивысшая степень точности квадратурных формул.

(1).

Формула (1) имеет неизвестных параметра: , - узлы квадратурной формулы, , - коэффициенты квадратурной формулы. Поэтому можно потребовать, чтоб квадратурная формула (1) была точной для любого алгебраического многочлена степени или что то же самое, чтоб она была точной для всех элементарных алгебраических многочленов ( функции). В формуле (1) в качестве функции возьмём и потребуем, чтоб для таких функций формула (1) была точной ( ):

(2).

Система равенств (2) представляет собой систему нелинейных алгебраических уравнений относительно неизвестных и , . Решение этой системы на практике затруднительно в силу её нелинейности, особенно, если порядок системы большой ( велико), поэтому будем строить квадратурные формулы алгебраической степени точности исходя из других соображений.

Теорема 1. Для того чтоб квадратурная формула (1) была точной для любого алгебраического многочлена степени не обходимо и достаточно:

1. чтоб она была интерполяционной: - узлы квадратурной формулы,

, (3).

2. чтобы многочлен был ортогонален с весом на отрезке интегрирования любому алгебраическому многочлену 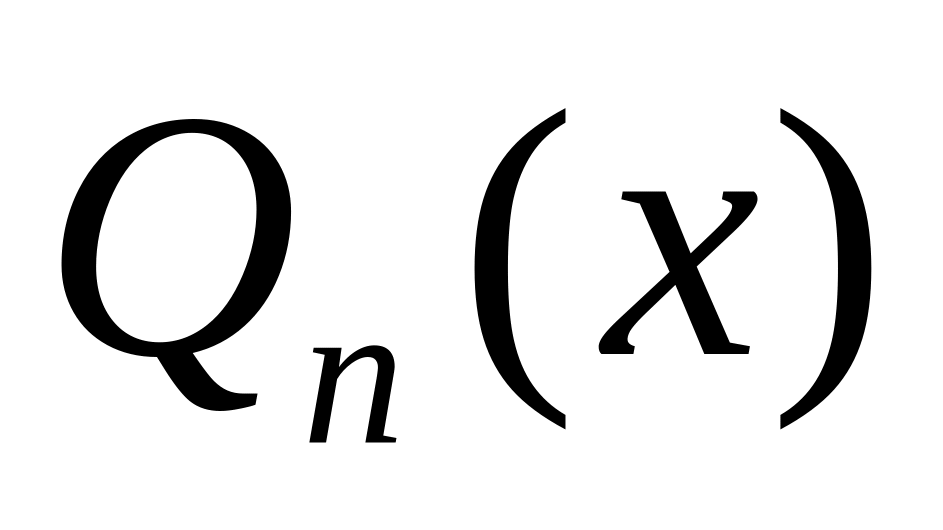степени , то есть 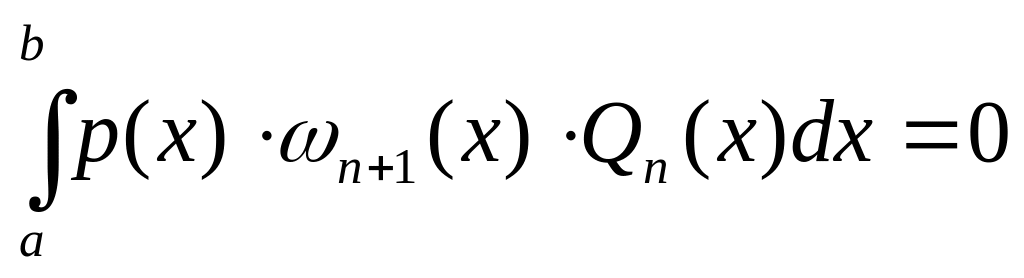(4).

Заметим, что из теоремы 1 вытекают следующие правила построения квадратурной формулы н.а.с.т.:

1. Построить алгебраический многочлен степени вида: (5) ортогональный с весом на отрезке любому алгебраическому многочлену степени .

2. найти корни многочлена 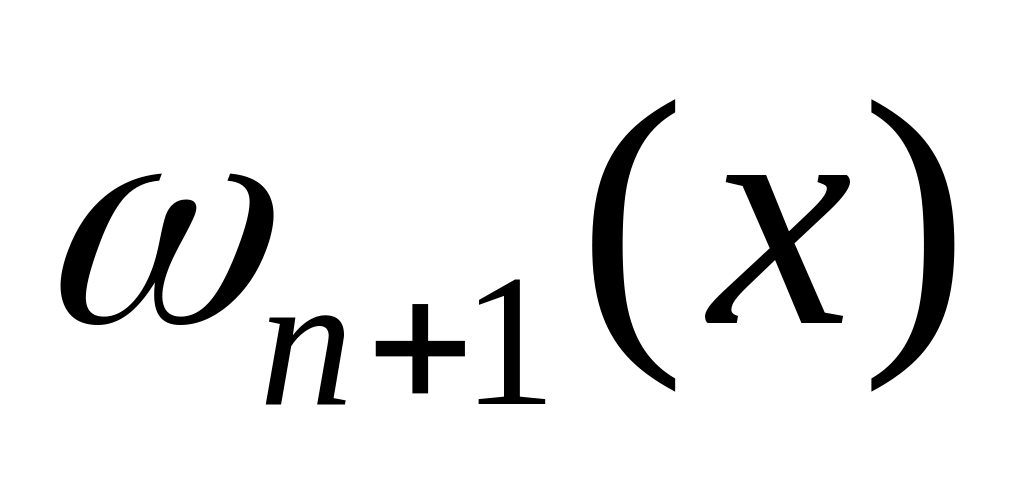и взять их в качестве узлов квадратурной формулы (1) ( - корень).

3. коэффициенты , формулы (1) вычислить по формуле (3).

Понятно, что самым сложным является реализация пункта 1, то есть построение многочлена .

Возможность построения многочлена с указанными свойствами даёт следующая теорема.

Теорема 2. Если весовая функция не меняет знак на отрезке интегрирования (для определённости ), то существует единственный многочлен вида (5) ортогональный с весом на отрезке любому алгебраическому многочлену степени .

Замечание. Доказательство теоремы 2 является конструктивным и содержит способ построения многочлена , то есть способ отыскания его коэффициентов (смотри доказательство в текстах лекций Балашова С.Д.).

Теорема 3. Если весовая функция сохраняет свой знак на отрезке интегрирования и это многочлен ортогональный с весом на отрезке любому алгебраическому многочлену степени , тога его корни вещественны, различны и лежат внутри отрезка .

Из теорем 1–3 таким образом следует, что если весовая функция сохраняет свой знак на отрезке интегрирования (для определённости ), то квадратурная формула алгебраической степени точности существует и единственна для любого значения - целое, положительное.

Теорема 4. Если весовая функция сохраняет свой знак на отрезке интегрирования , то ни при каком выборе узлов и коэффициентов квадратурная формула (1) не может иметь алгебраическую степень точности .

Доказательство. Возьмём , и в качестве - степень многочлена . Рассмотрим . Так как сохраняет свой знак на отрезке интегрирования и знакопостоянная, то знакопостоянная на и не равна нулю.

Если , то интеграл от знакопостоянной функции равен нулю в том случае, если подынтегральная функция , тогда . С другой стороны рассмотрим квадратурную сумму: , следовательно , то есть квадратурная формула (1) для указанного многочлена степени не является точной. Следовательно н.а.с.т. квадратурной формулы равна .

Теорема 5 (о погрешности квадратурных формул н.а.с.т.). Если весовая функция сохраняет свой знак на отрезке интегрирования (для определённости ), а подынтегральная функция непрерывна на вмести со своими производными до -го порядка включительно, то такая, что погрешность квадратурной формулы н.а.с.т. имеет вид: (6).

Рассмотрим вопрос о сходимости квадратурного процесса н.а.с.т. Из приведенных выше теорем вытекает, что если весовая функция (знакопостоянная) на , то квадратурную формулу н.а.с.т. можно построить единственным образом для любого значения при этом соответствующие узлы и коэффициенты будут принимать свои зависимые от значения: .

Квадратурная формула (1) будет иметь вид: (7).

Определение. Говорят, что квадратурный процесс н.а.с.т. (7) сходится, если .

Теорема 6 (о сходимости). Если весовая функция на , непрерывна на и сам конечный, то квадратурный процесс н.а.с.т. (7) сходится.