
- •Лекции по курсу: «численные методы»
- •Приближение функций
- •Численное интегрирование
- •Квадратурные формулы Ньютона-Котеса
- •Частные случаи формул Ньютона-Котеса
- •Квадратурные формулы наивысшей алгебраической степени точности (н.А.С.Т.)
- •Квадратурная формула Гаусса (частный случай квадратурной формулы н.А.С.Т. При )
- •Смысл введения весовой функции
- •Приближённое решение алгебраических и трансцендентных уравнений
- •Методы решения систем линейных алгебраических уравнений (слау)
- •Приближённое решение проблемы собственных значений матрицы
Приближённое решение проблемы собственных значений матрицы
Постановка задачи
Пусть - квадратная матрица -го порядка.
Определение.
Ненулевой вектор
![]() называется собственным вектором матрицы
,
если
называется собственным вектором матрицы
,
если
![]() (1).
(1).
Число называется собственным значением матрицы , соответствующим собственному вектору .
Рассмотрим равенство
(1)
подробнее, перенесём всё в левую часть:
![]() ,
,
![]() -
представляет собой СЛАУ относительно
координат
вектора
,
где
-
представляет собой СЛАУ относительно
координат
вектора
,
где
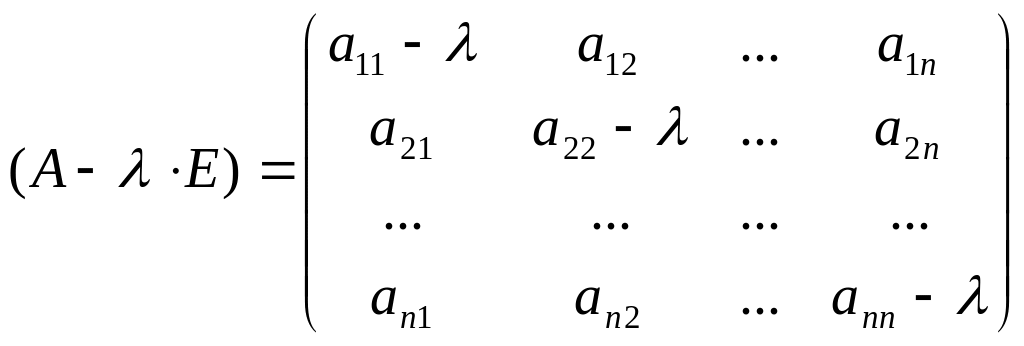
 (1`).
(1`).
Это однородная СЛАУ,
обладающая ненулевым решением,
следовательно
![]() (2).
(2).
На равенство (2)
можно смотреть как на уравнение
относительно
.
Это равенство называется характеристическим
уравнением матрицы
,
а
![]() называется характеристическим (вековым)
определителем матрицы
.
называется характеристическим (вековым)
определителем матрицы
.
Если непосредственно
раскрыть характеристический определитель,
можно получить следующее равенство:
![]() (2`),
где
(2`),
где
![]() -
сумма диагональных элементов матрицы
,
-
сумма диагональных элементов матрицы
,
![]() -
сумма диагональных миноров второго
порядка матрицы
и т.д.
-
сумма диагональных миноров второго
порядка матрицы
и т.д.
![]() .
.
Таким образом, видно,
что относительно собственных значений
![]() матрицы
имеем алгебраическое уравнение
-й
степени, причём среди которых могут
быть и комплексные даже и для вещественной
матрицы
.
матрицы
имеем алгебраическое уравнение
-й
степени, причём среди которых могут
быть и комплексные даже и для вещественной
матрицы
.
В дальнейшем, для
удобства, уравнение (2`)
будем записывать в виде:
![]() (2``).
На основе теоремы Виета можно записать
следующие равенства:
(2``).
На основе теоремы Виета можно записать
следующие равенства:
![]() ,
,
![]() .
.
Таким образом,
всякая
квадратная
матрица
-го
порядка имеет ровно
собственных значений, которые являются
корнями её характеристического уравнения
(2),
а собственные векторы матрицы получаются
как ненулевые решения СЛАУ (1`)
в которую вместо
подставляют собственное значение
![]() .
.
Из определения собственного вектора следует, что каждому собственному значению матрицы соответствует бесчисленное множество собственных векторов.
Пусть
собственный вектор матрицы
,
соответствующий собственному значению
:
![]() .
Рассмотрим вектор
.
Рассмотрим вектор
![]() (
(![]() ).
Подействуем матрицей
на вектор
).
Подействуем матрицей
на вектор
![]() :
:
![]() .
Следовательно,
также является собственным вектором
матрицы
,
соответствующий собственному значению
.
.
Следовательно,
также является собственным вектором
матрицы
,
соответствующий собственному значению
.
Такие векторы и являются линейно зависимыми и в дальнейшем различаться не будут. Мы будем отыскивать собственные векторы матрицы соответствующие собственным значениям с точность до постоянного множителя.
Матрица
может иметь не один, а несколько линейно
независимых собственных векторов
соответствующих собственным значениям
,
поскольку СЛАУ (1`)
имеет и может иметь несколько линейно
независимых решений при данном
(![]() -
количество линейно независимых
собственных векторов, где
-количество
уравнений, а
-
количество линейно независимых
собственных векторов, где
-количество
уравнений, а
![]() ).
).
Теорема 1.
Собственные вектора матрицы отвечающие
различным собственным значениям –
линейно независимы. То есть, если
![]() и
и
![]() собственный вектор
матрицы
соответствующий собственным значениям
собственный вектор
матрицы
соответствующий собственным значениям
![]() ,
,
![]() собственный вектор матрицы
соответствующий собственным значениям
собственный вектор матрицы
соответствующий собственным значениям
![]() ,
то
и
-
линейно независимые.
,
то
и
-
линейно независимые.
Следствие.
Если все собственные значения матрицы
:
различны,
то соответствующие
им
собственные
вектора
![]() (
(![]() )
в числе равном
образуют базис в соответствующем
-мерном
пространстве.
)
в числе равном
образуют базис в соответствующем
-мерном
пространстве.
Теорема 2.
Для того чтоб существовал базис из
собственных векторов матрицы
необходимо и достаточно, чтоб каждому
собственному значению матрицы
![]() соответствовало ровно
линейно независимых собственных
векторов, где
- кратность данного собственного
значения, как корня характеристического
уравнения.
соответствовало ровно
линейно независимых собственных
векторов, где
- кратность данного собственного
значения, как корня характеристического
уравнения.
Приведём полезные теоремы для матриц частного вида:
Симметричная матрица:
Теорема 3. Все собственные значения симметричной вещественной матрицы – вещественны.
Теорема 4.
Собственные вектора симметричной
вещественной матрицы соответствующие
собственным значениям взаимно
ортогональны:
![]() ,
где
,
где![]() ,
то
,
то
![]() .
.
Теорема 5.
Каждому собственному значению
![]() симметричной вещественной матрицы
соответствует ровно
взаимно ортогональных, а значит линейно
независимых собственных векторов, где
- кратность данного собственного
значения, как корня характеристического
уравнения данной матрицы.
симметричной вещественной матрицы
соответствует ровно
взаимно ортогональных, а значит линейно
независимых собственных векторов, где
- кратность данного собственного
значения, как корня характеристического
уравнения данной матрицы.
Следствие. Собственные вектора симметричной вещественной матрицы образуют ортогональный базис в соответствующем -мерном пространстве.
Теорема 6.
(Экстремальное свойство собственных
значений) Пусть
симметричная вещественная матрица:
![]() ,
,
![]() .
Тогда для
.
Тогда для
![]() :
:
![]() .
.
Положительно определённая матрица:
Теорема 7.
Для того чтоб симметричная матрица
была положительно определённой необходимо
и достаточно, чтоб все её собственные
значения
![]() .
.
Подобные матрицы:
Определение.
Две квадратные матрицы одного порядка
и
называются подобными, если существует
невырожденная матрица
такая, что выполняется условие:
![]()
Теорема 8. Подобные матрицы имеют одинаковые собственные значения.
{ Самостоятельно доказать теоремы 3–8}
Все методы решения проблемы собственных значений матрицы делятся на:
прямые – метод Крылова, метод Данилевского;
итерационные – метод Мизеса, метод вращений и другие.
Не ограничивая общности,
в дальнейшем будем считать, что
- вещественная квадратная матрица
-го
порядка. Из равенства (2`)
видно, что для непосредственного
раскрытия характеристического
определителя матрицы
:
требуется вычислить порядка
![]() различных определителей.
различных определителей.
Поэтому для раскрытия характеристического определителя часто используются другие более экономные приёмы.
Метод Крылова – прямой метод нахождения собственных значений и собственных векторов матрицы
Рассмотрим метод
Крылова раскрытия характеристического
определителя. Обозначим через
![]() с точностью до знака характеристический
полином матрицы
:
с точностью до знака характеристический
полином матрицы
:
![]() (1).
(1).
Поставим задачу
нахождения
![]() - коэффициентов
характеристического
полинома.
- коэффициентов
характеристического
полинома.
Теорема
(Гамильтона-Кели).
Всякая квадратная матрица
-го
порядка обращает в ноль свой
характеристический полином. То есть,
если подставить в равенство (1)
вместо
матрицу
,
то равенство нулю будет выполняться:
![]() (2),
где
(2),
где
![]() - нулевая матрица.
- нулевая матрица.
Выберем произвольный
ненулевой вектор
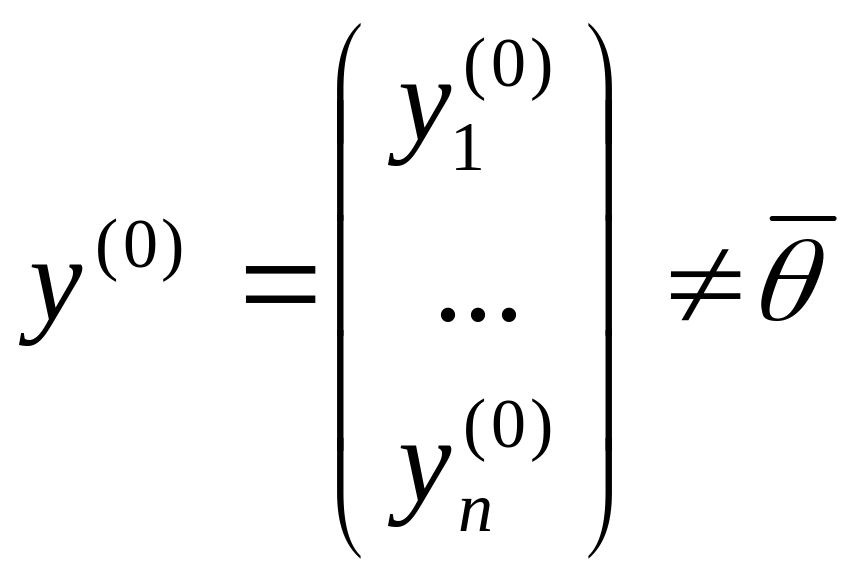 и умножим равенство (2)
на вектор
и умножим равенство (2)
на вектор
![]() справа, получим:
справа, получим:
![]() (3),
где
- нулевой вектор.
(3),
где
- нулевой вектор.
Введём обозначения:
![]() ,
,
![]() ,…,
,…,
![]() .
.
С учётом этих обозначений
формула (3)
перепишется:
![]() или что то же самое
или что то же самое
![]() (4).
(4).
Из формул для нахождения
векторов
![]() следует, что координаты вектора
вычисляются по следующей формуле:
следует, что координаты вектора
вычисляются по следующей формуле:
![]() .
.
Поэтому равенство (4) в координатной форме имеет вид:
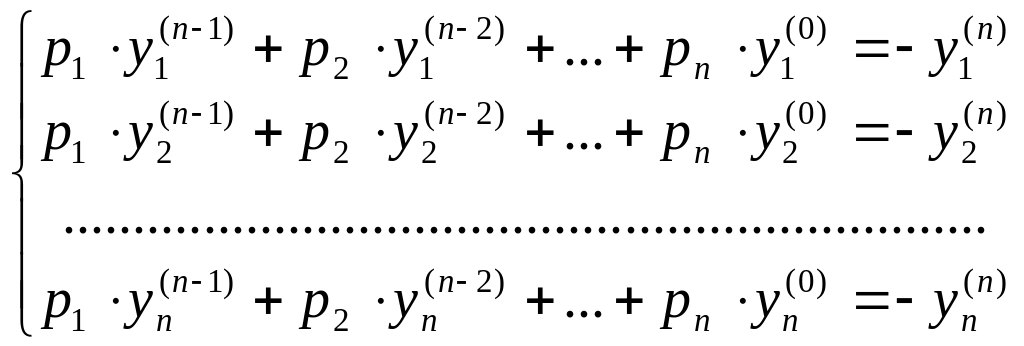 (4`).
(4`).
(4`) представляет собой СЛАУ относительно искомых коэффициентов характеристического полинома, которая может быть решена любым известным методом.
Если
![]() системы (4`)
оказывается
равным нулю, то выбор вектора неудачен.
Рекомендуется выбрать другой вектор и
проделать указанную выше работу ещё
раз.
системы (4`)
оказывается
равным нулю, то выбор вектора неудачен.
Рекомендуется выбрать другой вектор и
проделать указанную выше работу ещё
раз.
Таким образом, зная
коэффициенты
характеристического
полинома
можна теперь
любым
известным
методом решения
нелинейных
алгебраических
уравнений
отыскать
все собственные
значения
![]() матрицы
.
матрицы
.
Метод Крылова позволяет также находить собственные вектора соответствующие данным собственным значениям матрицы.
