Квадратурная формула Гаусса (частный случай квадратурной формулы н.А.С.Т. При )
Не ограничивая общности,
будем считать, что отрезок интегрирования
,
,
,
.
Будем
строить
квадратурную
формулу вида:
(8).
Квадратурную
формулу Гаусса
будем
строить
исходя из
алгоритма, вытекающего из теорем 1 – 3.
В соответствии с первым пунктом надо
построить алгебраический многочлен
ортогональный с весом
на
многочлену
степени
.
Условие (4)
.
С этой целью введём обозначение:
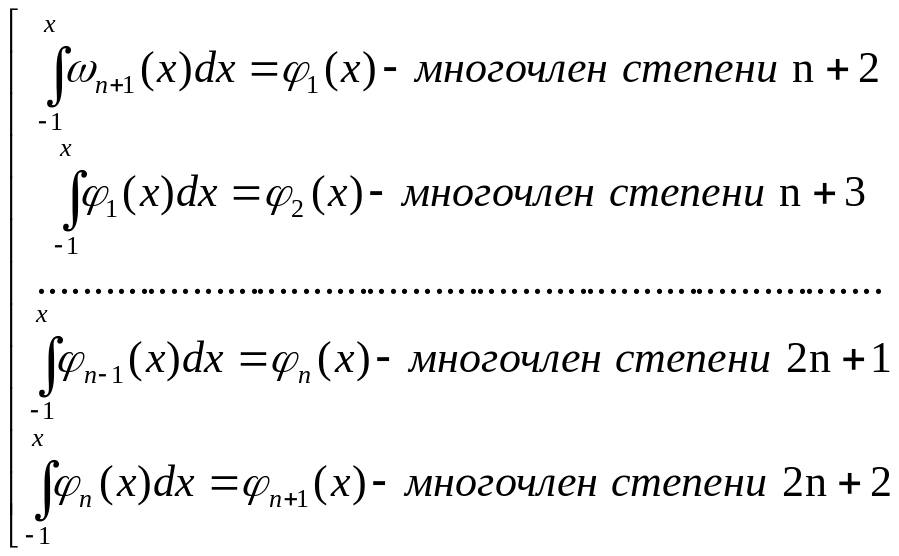(9).
Сразу заметим, что
(10).
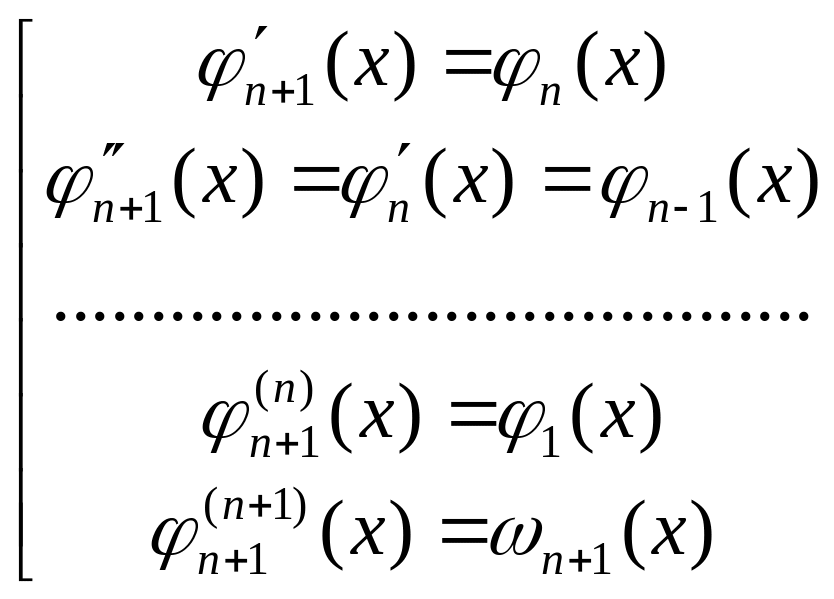(11).
Если мы построим
и продифференцируем её
раз, то получим
.
Будем вычислять
с помощью
формулы
интегрирования
по частям:
.
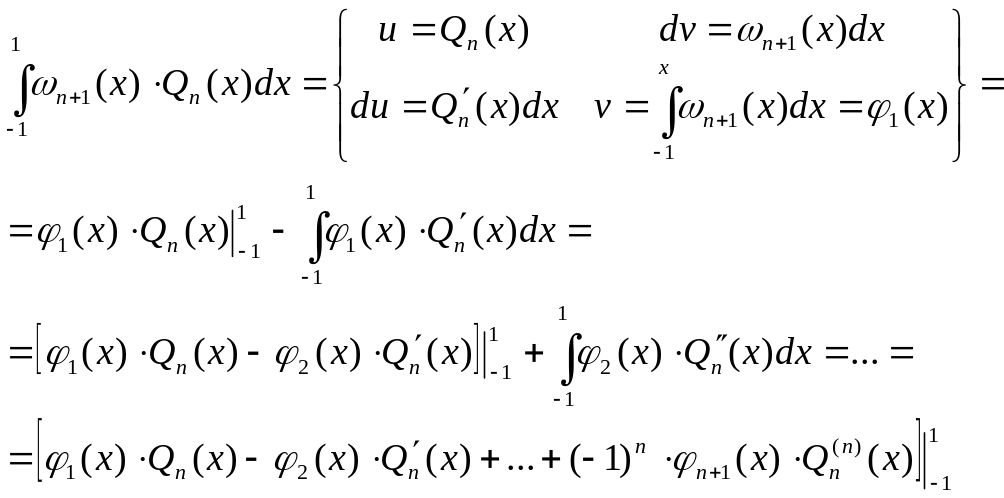(12).
Потребуем, чтоб
выполнялось условие ортогональности
(4),
то есть правая часть равенства (12)
обращалась в ноль. Заметим, что при
правая
часть
равна
нулю в силу равенства
(10).
В силу произвольности многочлена
,
правая часть равенства (12)
при
обязана быть
равна нулю.
То есть
(13).
Определение.
Точка
называется
корнем
функции
кратности
,
если сама функция в этой точке равна
нулю
,
а так же и
,
а
.
Поэтому, из этого определения из формул
(10),
(11) и
(13) следует,
что в точках
и
функция
,
обладает
корнями
кратности
.
Поскольку сама функция
является алгебраическим многочленом
степени
,
его можно представить в виде:
,
где
подлежащая определению.
Из формулы (11)
следует, что
(14).
Константу
найдём из требования, чтоб коэффициент
при старшей степени
многочлена
был равен единице (смотри формулу (5)).
Коэффициент при старшей степени
в правой части формулы (14)
равен:
,
подставляя в (14)
находим:
(15).
Искомый многочлен носит название многочлена Лежандра -й степени на отрезке .
Корни этого
многочлена на основании
теоремы
3. В силу того, что
весовая функция
,
то все корни
многочлена Лежандра (15)
вещественны, различны и лежат внутри
отрезка
,
поэтому
найденные
любыми известными
методами, например, методом половинного
деления, МПИ, методом хорд, методом
касательных, эти корни могут быть взяты
в качестве узлов квадратурной формулы
(8).
Коэффициенты квадратурной
формулы (8)
по известным узлам можно вычислить с
помощью формулы (3):
,
(16).
Таким образом имеем:
(17)
– квадратурная формула Гаусса на
,
где
вычисляются по формуле (16),
а
- корни многочлена Лежандра. Алгебраическая
степень точности данной квадратурной
формулы равна
.
Остаточный член формулы (17)
получается как частный случай формулы
(6),
в которой в качестве веса
,
а
и в качестве
многочлена
выступает многочлен Лежандра.
Замечание 1. Из формул для нахождения узлов и коэффициентов формулы Гаусса видно, что они не зависят от подынтегральной функции и от отрезка интегрирования. То есть узлы и коэффициенты квадратурной формулы Гаусса заранее вычислены и при небольших приведены в специальной литературе.
Замечание 2. Квадратурная формула Гаусса на произвольном отрезке имеет вид:
(18),
где
, вычисляются по формуле (16), а - корни многочлена Лежандра -й степени на отрезке .