
-
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования
Московский государственный институт электроники и математики
(технический университет)
Вычисление интегралов
Методические указания
для выполнения лабораторных работ и домашних заданий
по дисциплине "Информационные технологии 1"
Направление подготовки: 654700 – Информационные системы
Номер специальности: 071900 – Информационные системы и технологии
Факультет Прикладной математики
Кафедра
"Математическое обеспечение систем обработки информации и управления"
Автор: к.т.н., доцент Калинин Б.Н.
Москва – 2005 г.
Лабораторная работа
Вычисление интегралов
Требуется выполнить два задания.
а) Построить график изменения подинтегральной функции. Вычислить интеграл с помощью формул Гаусса и Ньютона-Котеса, предварительно выбрав весовую функцию и определив узлы интерполяции и коэффициенты интерполяционной формулы. Расчет провести для трех и четырех узлов. В случае бесконечных пределов интегрирования крайние узлы в формуле Ньютона-Котеса располагать в тех же точках, что и узлы формулы Гаусса. Для каждого из методов найти погрешность вычислений, сравнив результаты расчетов с точным значением интеграла.
б) Построить график изменения подынтегральной функции. Вычислить интеграл, используя составную формулу Симпсона, а также формулу Симпсона совместно с процессом Эйткена. Найти эффективный порядок формулы. Для каждого из методов найти погрешность вычислений. Проверить, как меняется погрешность вычислений при изменении числа подотрезков, на которые делится отрезок интегрирования.
Замечание.
Программы
Mathcad
и Mathematica
по умолчанию не раскрывают неопределенности
вида
![]() Во избежание ошибок в точках, где имеют
место неопределенности, следует в явном
виде вычислять пределы.
Во избежание ошибок в точках, где имеют
место неопределенности, следует в явном
виде вычислять пределы.
Для получения зачета студент должен продемонстрировать на экране компьютера действующую программу, реализующую решение поставленных задач. Студент должен уметь объяснить все детали представленной программы и ответить на связанные с темой теоретические вопросы.
Методические указания
Квадратурные формулы Гаусса и Ньютона-Котеса являются формулами интерполяционного типа. Эти формулы выводятся путем замены подинтегральной функции интерполяционным многочленом Лагранжа и интегрирования этого многочлена. При этом часто в подинтегральном выражении предварительно выделяют положительный сомножитель – весовую функцию – учитывающий особенности подинтегральной функции. Формулы могут быть представлены в виде:
![]() (1)
(1)
Здесь
(x)0
– весовая функция, а коэффициенты
![]() определяются формулой:
определяются формулой:
![]() ,
(2)
,
(2)
где
![]()
Цель введения весовой функции состоит в повышении точности квадратурной формулы путем учета особенностей подинтегральной функции. Например, при вычислении интеграла
![]() ,
,
где
f(x)
- гладкая функция, не равная нулю в точке
x=0,
целесообразно выделить в качестве
весовой функцию
![]() ;
тогда коэффициенты C
определяются по формуле (2) с учетом
особенности подинтегральной функции
в начальной точке отрезка интегрирования.
Если подинтегральная функция не имеет
особенностей, то следует положить (x)
1.
;
тогда коэффициенты C
определяются по формуле (2) с учетом
особенности подинтегральной функции
в начальной точке отрезка интегрирования.
Если подинтегральная функция не имеет
особенностей, то следует положить (x)
1.
Формулы Ньютона-Котеса строятся на равномерной сетке узлов:
![]()
Различают
формулы замкнутого
типа,
если
![]() и
и
![]() ,
и формулы разомкнутого
типа,
если хотя бы один из концевых узлов не
совпадает с соответствующей граничной
точкой отрезка интегрирования. Формулы
Ньютона-Котеса, построенные для n
узлов, точны для любого многочлена
степени меньше n.
Подставив в формулу (1) многочлен нулевой
степени f(x)1,
получим условие нормировки коэффициентов:
,
и формулы разомкнутого
типа,
если хотя бы один из концевых узлов не
совпадает с соответствующей граничной
точкой отрезка интегрирования. Формулы
Ньютона-Котеса, построенные для n
узлов, точны для любого многочлена
степени меньше n.
Подставив в формулу (1) многочлен нулевой
степени f(x)1,
получим условие нормировки коэффициентов:
![]() .
(3)
.
(3)
Квадратурные
формулы Гаусса,
или квадратурные
формулы наивысшей алгебраической
степени точности
строятся для неравномерной сетки узлов.
Узлы интерполяции xk
и коэффициенты
![]() выбираются так, чтобы формулы были точны
для любого алгебраического многочлена
степени m
2·n–1.
Это означает, что
выбираются так, чтобы формулы были точны
для любого алгебраического многочлена
степени m
2·n–1.
Это означает, что
![]() ,
,
![]() удовлетворяет системе уравнений:
удовлетворяет системе уравнений:
![]() (4)
(4)
Решение системы (4) дает один из способов нахождения параметров формулы Гаусса. Отметим, что первое из уравнений системы совпадает с условием нормировки коэффициентов (3).
Обозначим
через![]() многочлен,
корнями которого являются узлы
интерполяции:
многочлен,
корнями которого являются узлы
интерполяции:
![]() (5)
(5)
Для формулы Гаусса справедливо следующее утверждение: многочлен ортогонален с весом (x) любому многочлену q(x) степени меньше n, т.е.
![]() ;
(6)
;
(6)
Условие
ортогональности (6) эквивалентно
требованиям:![]()
![]() (7)
(7)
которые
представляют собой систему уравнений
относительно неизвестныx
![]() Отсюда следует второй способ
нахождения параметров формулы Гаусса:
положение узлов интерполяции определяется
из системы (7), а коэффициенты
вычисляются по формуле (2), либо путем
решения системы (4), в которой в данном
случае достаточно оставить только n
уравнений.
Отсюда следует второй способ
нахождения параметров формулы Гаусса:
положение узлов интерполяции определяется
из системы (7), а коэффициенты
вычисляются по формуле (2), либо путем
решения системы (4), в которой в данном
случае достаточно оставить только n
уравнений.
Если весовая функция четна относительно середины отрезка интегрирования, то есть
[(a + b)/2 – y] = [(a + b)/2 + y] при 0 y (b – a)/2, или, иначе,
[x] = [a + b – x] при a x b,
то формула Гаусса является симметричной: узлы формулы расположены симметрично относительно центра отрезка, а коэффициенты попарно равны:
(a
+ b)/2
–
![]() =
=![]() –
(a
+ b)/2
или
=
a
+
b
–
,
–
(a
+ b)/2
или
=
a
+
b
–
,
![]() =
,
k = 1, . . ,m,
=
,
k = 1, . . ,m,
где
m есть целая часть частного n/2. Если число
узлов – нечетно:
![]() то
то
![]() =
(a
+ b)/2,
а коэффициент
=
(a
+ b)/2,
а коэффициент
![]() может быть определен из условия нормировки
может быть определен из условия нормировки
![]() .
.
Таким образом, при наличии четной весовой функции количество уравнений в системах (4) и (7) может быть уменьшено не менее чем в два раза.
Произвольный отрезок интегрирования [a, b] можно привести к стандартному отрезку [-1, 1] линейным преобразованием:
t = -1 + (x – a)·2/(b – a), x = a + (t + 1)(b – a)/2
Если a= -1, b=1, то для симметричных формул имеем:
![]() ,
,
![]()
Напомним, что интеграл в симметричных пределах от нечетной функции равен нулю. Так, например,
![]()
независимо от значений , k = 1, . . ,m. Поэтому в случае симметричного отрезка интегрирования для нахождения узлов формулы Гаусса следует использовать только те из уравнений (7), в которых подинтегральная функция является четной функцией x.
Из
условия ортогональности (6) следует, что
многочлены
![]() ,
описывающие узлы формулы Гаусса, образуют
ортогональную систему:
,
описывающие узлы формулы Гаусса, образуют
ортогональную систему:
![]() ,
n
m.
,
n
m.
Для ряда весовых функций известны соответствующие ортогональные системы многочленов и формулы, позволяющие непосредственно вычислять положение узлов и коэффициенты формулы Гаусса.
Рассмотрим типичные примеры.
1.
(x)
1, a
= -1, b
= 1.
В этом случае узлы формулы Гаусса
совпадают с корнями многочлена
Лежандра
![]() :
:
![]() ,
,
![]() ,
,
![]() .
.
Для многочленов Лежандра существует рекуррентная формула:
![]() .
.
Значения коэффициентов можно определить по формуле:
![]()
2.
(x)
= 1/![]() ,
a
= -1, b
= 1.
Узлы квадратурной формулы Гаусса
совпадают с корнями многочленов
Чебышева первого рода
T(x)
и весовые коэффициенты для всех узлов
одинаковы:
,
a
= -1, b
= 1.
Узлы квадратурной формулы Гаусса
совпадают с корнями многочленов
Чебышева первого рода
T(x)
и весовые коэффициенты для всех узлов
одинаковы:
![]() =
Cos(n·arcCos(x)),
=
Cos[(2k-1)/(2n)],
=
Cos(n·arcCos(x)),
=
Cos[(2k-1)/(2n)],
![]() =
/n,
k = 1, .
.
,n.
=
/n,
k = 1, .
.
,n.
3. (x) = , a = -1, b = 1. Узлы квадратурной формулы Гаусса совпадают с корнями многочленов Чебышева второго рода:
![]() =
Sin[(n+1)·arcCos(x)]/Sin[arcCos(x)],
=
Sin[(n+1)·arcCos(x)]/Sin[arcCos(x)],
Узлы многочленов расположены в точках
= Cos[k·/(n+1)], k = 1, . . ,n
Например, при n=3:
![]()
Вообще для данной весовой функции условие нормировки коэффициентов формулы Гаусса имеет вид:
![]()
4.
(x)
= exp(![]() ),
a
= –,
b
= .
Узлы квадратурной формулы Гаусса
совпадают с корнями многочленов
Эрмита:
),
a
= –,
b
= .
Узлы квадратурной формулы Гаусса
совпадают с корнями многочленов
Эрмита:
![]() =
1,
=
1,
![]()
![]() или
или
![]()
Весовые коэффициенты могут быть вычислены по формулам:
![]() .
.
5.
(x)
=
![]() ·exp(
·exp(![]() ),
a
= 0, b
= .
Узлы квадратурной формулы Гаусса
совпадают с корнями многочленов
Лагерра:
),
a
= 0, b
= .
Узлы квадратурной формулы Гаусса
совпадают с корнями многочленов
Лагерра:
![]()
![]()
![]()
![]() .
.
Весовые коэффициенты могут быть вычислены по формулам:
![]()
(x) =
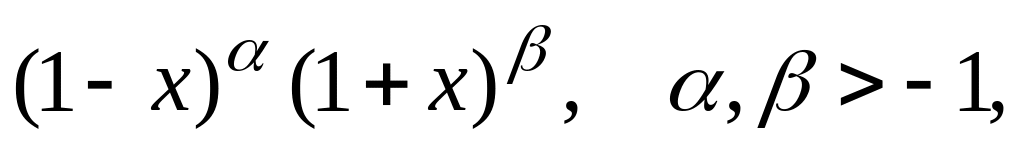 a
= –1,
b
= 1.
Узлы формулы Гаусса совпадают с корнями
многочленов
Якоби:
a
= –1,
b
= 1.
Узлы формулы Гаусса совпадают с корнями
многочленов
Якоби:
![]() .
.
В
частном случае, при ,
-1/2,
(x)
=
![]() первые три многочлена Якоби имеют вид:
первые три многочлена Якоби имеют вид:
![]()
Формула Ньютона-Котеса замкнутого типа при n=3 и (x)1:
![]() h
= b – a,
–
h
= b – a,
–
называется
простой
формулой Симпсона.
Для повышения точности расчетов отрезок
интегрирования часто разбивают на
несколько подотрезков. Пусть отрезок
[a,
b]
разбит на m частей так, что
![]() ,
,
![]() ,
i=0,..,m-1 и
,
i=0,..,m-1 и
![]() .
Формула
.
Формула
![]()
называется составной формулой Симпсона. Для подинтегральной функции, имеющей непрерывную четвертую производную, формула Симпсона имеет четвертый порядок точности; главный член погрешности определяется соотношением:
![]()
Если
подинтегральная функция имеет какие-либо
особенности, то порядок точности
квадратурной формулы снижается. Так,
для формулы Симпсона эффективный порядок
может быть менее четырех. В подобных
случаях для повышения точности расчетов
и для определения значения эффективного
порядка выбранной квадратурной формулы
используют процесс
Эйткена.
Для этого проводят расчеты с различным
шагом h
(или, иначе, с делением исходного отрезка
[a,
b]
на разное число частей). Обозначим:
![]() – результат расчетов при использовании
шага
– результат расчетов при использовании
шага
![]() ,
k=1;2;3, q
– целое число (например, q=2). Уточненное
значение интеграла определяется по
формуле:
,
k=1;2;3, q
– целое число (например, q=2). Уточненное
значение интеграла определяется по
формуле:
![]() .
.
Эффективный порядок квадратурной формулы оценивается соотношением
![]() .
.
