Министерство образования и науки российской федерации

Уральский филиал

федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Российский Экономический Университет им. Г.В. Плеханова»

Старший преподаватель Перминова Е.А.

Экономико–математические методы и модели

Екатеринбург

2011

Методическое руководство предназначено для проведения занятий и самостоятельной работы по курсу «Линейное программирование» для студентов дневного обучения. Работа содержит краткие теоретические сведения по изучаемым разделам, примеры решения задач, задания для курсовой или лабораторных работ студентов.

Руководство состоит из двух основных частей: «линейное программирование» и «транспортная задача линейного программирования». В первом разделе рассматриваются следующие темы: обзор основных задач линейного программирования, методы решения задач: геометрический, симплекс-метод, метод искусственного базиса. Также рассмотрены вопросы построения и решения двойственных задач ЛП.

Раздел «транспортная задача линейного программирования» содержит краткие сведения по теории оптимизации грузовых перевозок и назначений в распределительных задачах. При работе с данным руководством предполагается использование специально разработанных программных средств (ПС). Индивидуальные задания для студентов содержат задачи, требующие как умения решать задачи «вручную», так и с использованием указанных ПС. Руководство составлено в соответствии с учебным планом и предназначено для проведения занятий со студентами всех специальностей дневного обучения.

Автор:

Перминова Е.А., ст. преподаватель,

Рецензент:

Скачков П.П., доцент кафедры «Высшая математика», УрГУПС

© Российская Экономическая Академия им. Г.В. Плеханова», 2011

Содержание

1. ОСНОВНЫЕ ПОНЯТИЯ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 4

Рассмотрим правила перехода от одной модели к другой. 5

1.1 Переход от стандартной модели ЗЛП к канонической 5

1.2. Переход от канонической модели задачи ЛП к стандартной 6

1.3. Переход от основной модели задачи ЛП к канонической 6

2. Геометрическая иллюстрация решения задач ЛП 7

3. Двойственность в задачах линейного программирования 10

3.1. Построение двойственных моделей 10

3.2. Теоремы двойственности 11

3.3. Экономическая интерпретация переменных двойственной задачи 13

4. Симплекс-метод в задачах ЛП 14

4.1. Основные положения симплекс-метода 14

4.2. Правило преобразования симплекс-таблиц 15

4.3. Геометрическая интерпретация симплекс-метода 18

5. Метод искусственного базиса 19

5.1. Постановка задачи 19

5.2. Теоремы метода 20

5.3. Примеры решения задач 20

Индивидуальные задания 26

6. ТРАНСПОРТНАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 28

6.1. Транспортная задача линейного программирования 28

6.1.1. Постановка задачи 28

6.1.2. Математическая модель 28

6.2. Методы определения начального опорного плана 29

6.2.1. Метод северо-западного угла 29

6.2.2. Метод наименьшей стоимости 30

6.2.3. Метод двойного предпочтения 31

6.3. Метод потенциалов 32

6.4. Построение цикла и определение величины перераспределения груза 32

6.5. Открытая транспортная задача 35

6.6. Проблема вырожденного плана задачи 36

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ 37

7. Задача об оптимальном назначении 38

7.1. Постановка задачи 38

7.2. Математическая модель 38

7.3. Решение задачи о назначениях венгерским методом 39

7.4. Решение задачи максимизации 41

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ 42

БИБЛИОГРАФИЧЕСКИЙ СПИСОК 43

Методы оптимизации

Оптимизационные задачи бывают двух типов: задачи минимизации и задачи максимизации, т.е. отыскание наименьшего или наибольшего значения целевой функции f(X) на допустимом множестве. Оптимизационная задача, в которой целевая функция является линейной, множество допустимых значений задается системой линейных уравнений или линейных неравенств, называется задачей линейного программирования.

При этом система линейных уравнений или линейных неравенств называется системой ограничений задачи линейного программирования.

1. Основные понятия линейного программирования

Линейное программирование (ЛП)  это раздел математики о методах исследования и поиска наибольших и наименьших значений некоторой линейной функции, причем ограничения задачи тоже линейны. Математические модели задач линейного программирования (ЗЛП) различаются между собой по виду ограничений.

Определение 1. Математическую модель ЗЛП будем называть стандартной, если ограничения в ней представлены в виде линейных неравенств, а целевая функция минимизируется или максимизируется.

Например, пусть в модели два неизвестных: х₁, х₂. Надо найти среди решений системы неравенств такие, которые дают целевой функции наибольшее (наименьшее) значение. Такая модель имеет вид:

(1.1)

(1.2),

где  искомое решение системы.

Здесь, система линейных неравенств, определяющая допустимое множество решений задачи (1.1), называется системой ограничений задачи линейного программирования, а линейная функция называется целевой функцией или критерием оптимальности.

Определение 2. Математическая модель ЗЛП называется основной, если ограничения в ней представлены в виде уравнений при условии неотрицательности переменных. Такая модель имеет вид:

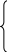
(1.3)

(1.4),

где  искомое решение системы.

Система уравнений (1.3) обычно имеет конечное множество решений. Целевая функция f(х) - линейная, поэтому частные производные постоянны, а это значит, что внутри области решений системы (1.3) экстремальных точек нет. Если целевая функция имеет оптимальное решение, то оно достигается в точках границ области.

Таким образом, в линейном программировании исследователя интересуют вершины многоугольника решений системы (1.3). Отсюда возникает вопрос: какой вид должна иметь модель ЛП, чтобы координаты вершин многоугольника решений могли быть легко получены? Рассмотрим другие модели задач линейного программирования.

Определение 3. Математическая модель называется канонической, если ее система ограничений представлена в виде системы m линейно независимых уравнений (ранг системы r = m), в системе выделен единичный базис, свободные переменные и целевая функция выражена через свободные переменные.

Запишем каноническую модель ЗЛП:

(1.6)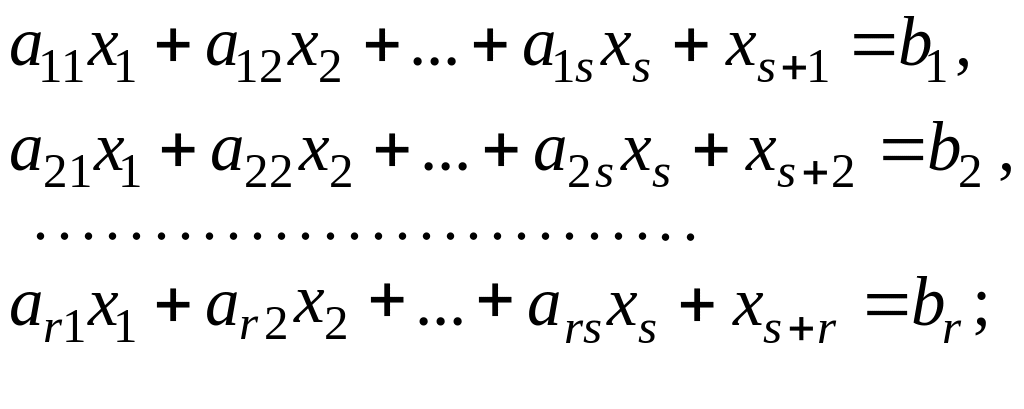

(1.5)

Определение 4. Будем называть переменные, входящие в одно из уравнений системы с коэффициентом один и отсутствующие в других уравнениях, базисными неизвестными, а все другие – свободными.

В нашей модели переменные x₁,...,х_{s _} – свободные, и, если их принять равными нулю, то из системы (1.5) легко получить значения базисных переменных x_s+1, x_s+2,..., x_s+r .

Определение 5. Решение системы называется базисным, если в нем свободные переменные равны нулю, и оно имеет вид:

_.

Базисное решение является угловой точкой множества решений системы (1.5), или, можно сказать, определяет вершину многоугольника решений модели. Среди таких решений находится и то, при котором целевая функция принимает оптимальное значение.

Определение 6. Базисное решение называется опорным, если оно допустимо, то есть все правые части уравнений (неравенств) положительны .

Теорема 1. Базисное опорное решение в канонической модели является оптимальным, если все коэффициенты в целевой функции не положительны, то есть .