11.4. Властивості операцій над матрицями.
Доведення всіх наведених нижче властивостей пропонується у якості вправ для самостійного опрацювання.
Властивості операцій множення матриці на число і додавання матриць є абсолютно такими ж самими, як і властивості відповідних операцій над векторами.
11.4.1. Асоціативність операції матричного множення:
11.4.2. Некомутативність операції матричного множення:
взагалі кажучи
;
це означає існування таких “конкретних”
числових матриць
і
(навіть квадратних), для яких виконується
вказана нерівність.
11.4.3. Адитивність по першому і другому множнику операції матричного множення:
11.4.4. Існування та єдиність нейтрального елемента відносно операції матричного множення .
Одинична матриця — це така квадратна матриця, у якої елементи з однаковими індексами дорівнюють 1, а решта — 0:
.
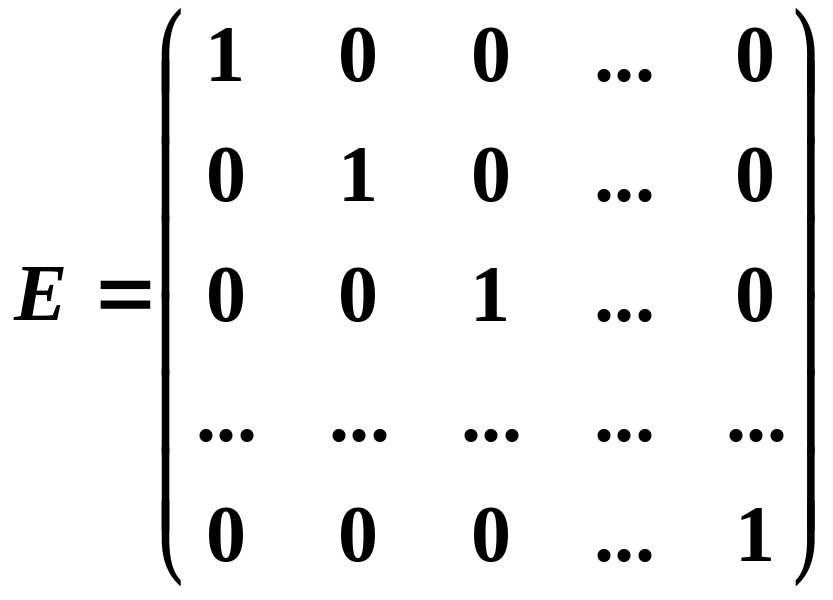Теорема
(про єдиність одиничної матриці). При
фіксованих розмірах одинична матриця
є єдиною матрицею з властивостями
нейтрального елемента. Тобто, якщо деяка
матриця
така, що для будь-якої матриці
,
то
.
Доведення.
Нехай виконується
умова теореми. Візьмемо за матрицю
одиничну матрицю, тоді
.
Але ми тільки що довели, що для будь-якої
матриці
:
,
значить
повинно дорівнювати
.
Отже
.
Про таку властивість говорять, що - є нейтральним елементом відносно операції матричного множення.
Зауваження: аналогічну властивість відносно додавання матриць має нульова матриця.
11.4.5. Анулююча властивість нульової матриці.
Нульова матриця:
—
це така матриця, всі елементи якої дорівнюють нулю.
1)Якщо матрицю
і деяку нульову матрицю можна перемножити,
то в результаті отримаємо нульову
матрицю
.
2) Аналогічно:
.
3) Більш загальний факт.
Нехай матриця має нульовий -тий рядок.
Якщо дану матрицю і деяку матрицю можна помножити, то -й рядок добутку буде нульовим.
4)Аналогічно: якщо матриця має нульовий -й стовпчик, якщо матрицю можна помножити (зліва) на таку матрицю , то добуток буде мати нульовий і-й стовпчик.
Із 3) і 4) твердження випливає 1) і 2).
11.5. Мультиплікативна форма методу Гауса
Основний висновок, який ми отримаємо: замість того, щоб виконувати елементарні перетворення над рядками деякої матриці, можна цю матрицю помножити зліва на підходящу квадратну матрицю. Цю матрицю-множник можна отримати виконавши відповідні елементарні перетворення над одиничною матрицею.
Приклад.
Виконаємо ці перетворення над одиничною матрицею (3х3).
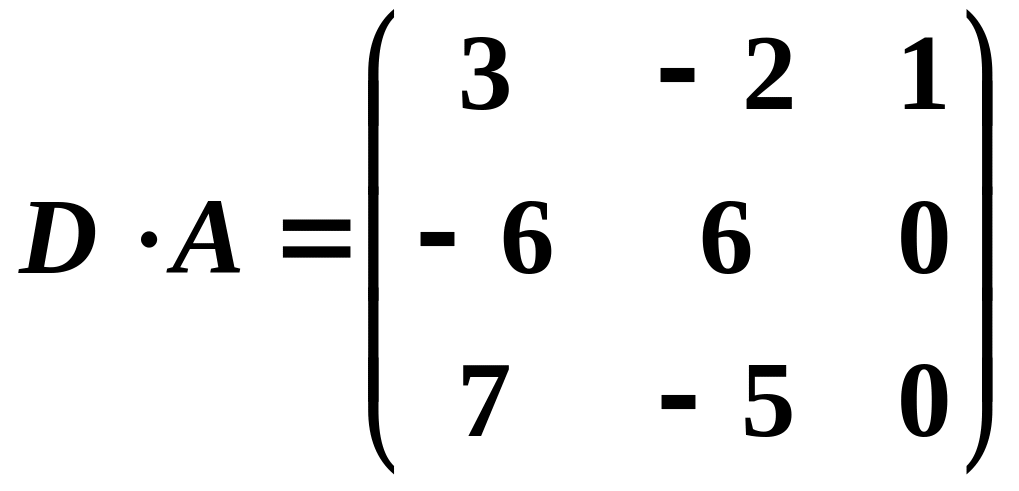
Таким чином, виконуючи елементарні перетворення над одиничною матрицею, ми утворюємо матрицю, яка начебто “запам’ятала” ці перетворення і при множенні на іншу матрицю їх “згадує”.
11.6.Обернена матриця, її обчислення і застосування.
11.6.1. Поняття оберненої матриці.
Означення (оберненої матриці). Нехай і — дві квадратні матриці ( ). Матриця називається оберненою до , якщо виконується
.
Обернена матриця
позначається
.
Теорема (про єдиність оберненої матриці). Нехай фіксована квадратна матриця. Якщо для неї існує обернена, то тільки одна.
Доведення. Припускаємо
супротивне. Нехай існують матриці
і
,
такі що:
Розглянемо добуток
.
,
=
.
Не кожна матриця
має обернену. Можна довести, що матриця
має обернену матрицю
тоді і тільки тоді, коли визначник
матриці
не дорівнює нулю. Поки що загальне
поняття визначника не введене, тому
сформульоване твердження, а також
викладені нижче положення можна вважати
такими, що стосуються матриць розмірів
і
.
Обернену матрицю до матриці можна знаходити двома способами.
11.6.2. Формула для обчислення оберненої матриці:
,
де
-
алгебраїчні доповнення елементів
матриці
(див. §
12).
11.6.3. Обчислення оберненої матриці методом Гауса.
Нехай - деяка квадратна матриця.
Утворимо розширену матрицю
,
приписавши справа до даної матриці одиничну.
Над розширеною матрицею виконаємо елементарні перетворення виключення, які ліву половину (тобто матрицю ) переведуть в одиничну матрицю, тоді друга половина перетвориться в обернену для :
Приклад 1.
Приклад 2. (знаходження оберненої матриці за детермінантною формулою).
Впевнимося, що матриця має обернену.
Отже має обернену, знайдемо її за допомогою формули. У даному випадку алгебраїчними доповненнями до елементів матриці будуть:
; 
; 
;
; 
; 
;
; 
; 
.
Таким чином, одержали
.
Приклад 3. (знаходження оберненої матриці методом Гауса).
.
.
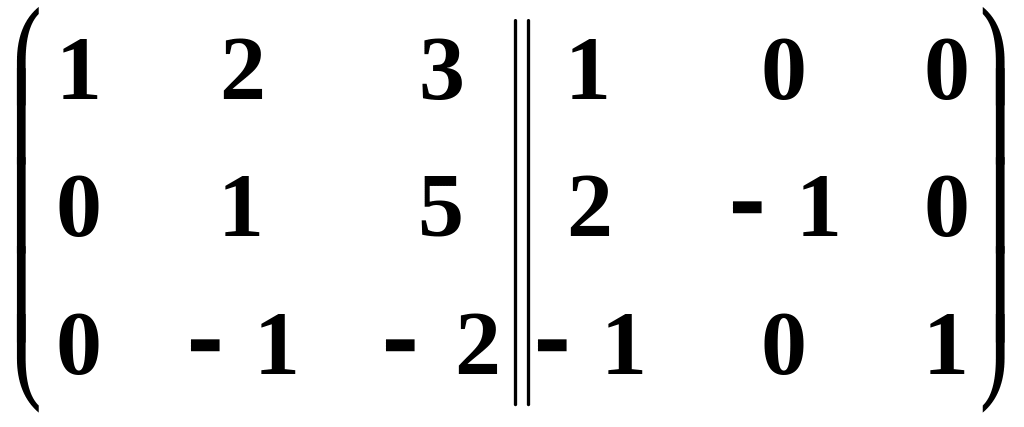
Якщо матриця квадратна другого порядку
,
визначник якої
,
то обернену до неї можна знайти за
формулою:
.
Приклад.
.