13.1. На підходах до поняття лінійної залежності і незалежності.

Значення поняття лінійної залежності і незалежності полягає в тому, що воно висвітлює єдину сутність багатьох, здавалося б різнорідних понять. З розгляду деяких з них ми і почнемо.

13.1.1.Колінеарність векторів.

Поняття колінеарності дуже близьке за змістом до поняття паралельності і вживається стосовно вільних векторів в аналітичній геометрії (див. §3): вільні вектори немов би „невловимі”, їх можна вільно пересувати паралельно; конкретний вектор, тобто направлений відрізок, можна розглядати як представника, миттєве положення вільного вектора; усі такі представники мають однакові величини проекцій на координатні осі, які приймаються за координати вільного вектора. Так от, якщо ми говоримо про два колінеарні вектори і , то можна собі уявляти, що ми упіймали ці вектори, сумістили їх початки, і тоді вектори уляглися на одній прямій, а тоді ми згадали, що є така операція векторної алгебри: множення вектора на число

Нехай два вільні вектори і задані своїми координатами: . Векторна алгебра дає алгебраїчний критерій колінеарності:

вектори і колінеарні (позначаємо ) тоді і тільки тоді, коли один з них можна отримати з іншого множенням на деяке число (тобто розтягуванням або стисканням):

.

13.1.2. Компланарність векторів.

Три вектори називаються компланарними, якщо при суміщенні їх початків вони потрапляють у деяку площину. Між компланарними векторами існує цікаве співвідношення. Нехай – компланарні (вільні) вектори. Розглянемо малюнок у припущенні, що початки векторів суміщені, і площина зображення є та сама площина, куди потрапили вектори:

Ми проілюстрували доведення такого твердження: якщо на площині є два не колінеарні вектори, то будь-який (інший) вектор на площині можна подати як суму цих (фіксованих) векторів, помножених на деякі числа:

.

Ми вже неодноразово зустрічались з поняттям лінійної комбінації системи векторів: це сума векторів, помножених на деякі числа (коефіцієнти). Отже, можна сказати, що вектор поданий як лінійна комбінація векторів і або ще так: вектор розкладений за векторами і .

13.1.3. Знаходження методом Гаусса рівнянь-наслідків.

Застосуємо метод Гаусса до СЛР:

Скористаємося тим, що в 1-у рівнянні є змінна з коефіцієнтом 1. Виключимо за допомогою першого рівняння змінну з 2-го і 3-го рівнянь перетвореннями:

(до 2-го додаємо перше рівняння, помножене на (-2),

до 3-го додаємо перше рівняння, помножене на (-7));

отримуємо:

Далі, до 3-го рівняння додаємо 2-ге, помножене на (-5). СЛР набуває такого вигляду:

Можна сказати, що 3-е рівняння після такого перетворення “зникає”. Це є показником того, що 3-є рівняння є наслідком перших двох. Дамо відповідь на питання: яким чином третє рівняння останньої СЛР утворене з рівнянь початкової СЛР? При його утворенні брали участь рівняння-результати першого повного перетворення виключення, отже, по відношенню до початкових рівнянь, ми виконували таке перетворення:

.

В цьому перетворенні рівняння відіграють роль особливих алгебраїчних величин, отриманий вираз подібний до алгебраїчного виразу

.

Розкриваємо дужки і зводимо подібні:

.

Згадуємо, що змінні в цій тотожності – це рівняння нашої СЛР. Тлумачимо тотожність в термінах рівнянь: якщо до 1-го рівняння, помноженого на 3, додати 2-е, помножене на (-5), і ще додати 3-є, то отримаємо тотожньо нульове рівняння. Або ще так: якщо до 1-го рівняння, помноженого на (-3), додати 2-е, помножене на 5, то отримаємо в точності 3-є рівняння (переконайтесь!):

,

інакше кажучи, 3-є рівняння є лінійною комбінацією1-го і 2-го рівнянь. А якби ми застосовували матричний варіант методу Гаусса, то отримали б такий висновок: 3-й рядок розширеної матриці СЛР є лінійною комбінацією1-го і 2-го рядків. От що означає, що якесь рівняння СЛР є наслідком інших рівнянь і що встановлює метод Гаусса, утворюючи на місці такого рівняння повністю нульове рівняння.

13.1.4. Векторний погляд на систему лінійних рівнянь.

Згадаємо другу векторну форму запису СЛР. В ній беруть участь стовпчики основної матриці (тобто зібрані у вектори-стовпчики коефіцієнти при кожній окремо змінній) і стовпчик вільних членів СЛР (див. §8):

,

, .

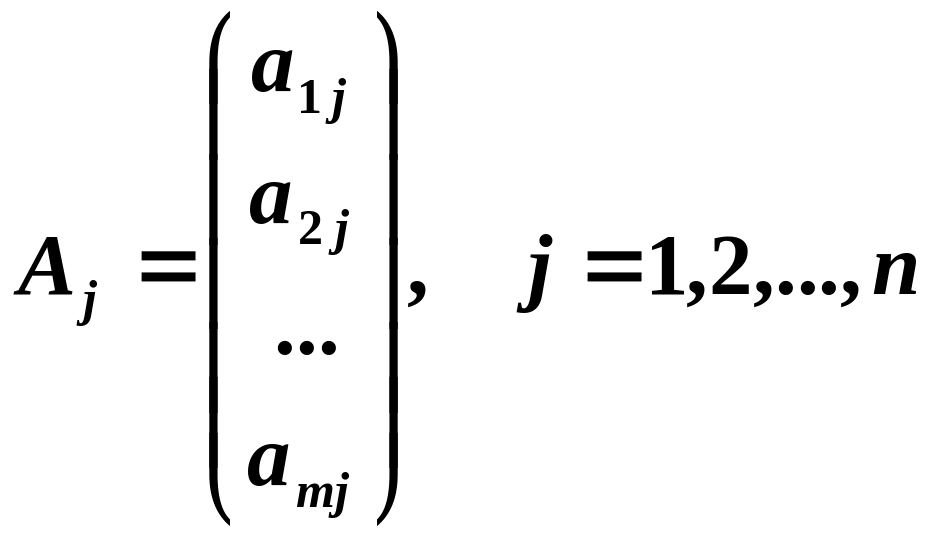Ліві частини рівнянь з СЛР утворюють лінійну комбінацію векторів з коефіцієнтами , і ця лінійна комбінація прирівнюється до стовпчика вільних членів. Такий запис з точки зору питання про сумісність СЛР (тобто існування хоча б одного розв’язку) можна інтерпретувати як питання: чи є вектор-стовпчик вільних членів СЛР лінійною комбінацією векторів-стовпчиків основної матриці СЛР ?