3.2.4. Методы глобальной оптимизации

При обучении НС с нелинейными функциями активации даже при решении относительно простых технических задач необходимо учитывать возможность появления большого количества локальных минимумов целевой функции. Например, если для одного нейрона с входным весом w₁ и весом поляризатора w₀ при линейной функции активации график зависимости от w₀, w₁ имеет вид выпуклой поверхности, единственный минимум которой легко определить при любых начальных условиях, то при использовании в качестве функции активации гиперболического тангенса форма принципиально меняется, изобилуя плоскими участками и множеством локальных минимумов. Увеличение размеров НС только осложняет проблему, поскольку число минимумов также возрастает, каждый из которых представляет собой ловушку на пути к глобальному минимуму, в котором принимает наименьшее значение.

Все рассмотренные до сих пор детерминированные методы обучения являются локальными, поскольку ведут к одному из локальных минимумов , лежащему в окрестности точки начала обучения. При этом оценить оптимальность найденного решения можно лишь в тех случаях, когда значение глобального минимума известно. Если локальное решение считается неудовлетворительным, то процесс обучения можно повторить, используя новые (как правило, случайные) начальные значения или изменяя случайным образом найденное ранее решение («встряхивание» весов). Подобный прием – применение стохастических алгоритмов к детерминированным методам обучения – связан с определенной вероятностью того, что новый поиск будет покидать «зоны притяжения» найденных ранее локальных минимумов. При решении реальных задач даже приблизительная оценка глобального минимума оказывается неизвестной, что требует, в общем, применения методов глобальной оптимизации, среди которых наиболее разработаны метод имитации отжига, генетические алгоритмы и метод виртуальных частиц.

3.2.4.1. Метод имитации отжига (ио)

Предложенный Н. Метрополисом в 1953 году, метод ИО представляет собой алгоритмический аналог физического процесса управляемого охлаждения, при котором кристаллизация расплава сопровождается глобальным уменьшением его энергии, причем допускаются ситуации кратковременного повышения энергетического уровня (например, при небольшом подогреве), способствующие выводу из ловушек локальных минимумов энергии, возникающих при реализации процесса. Классический алгоритм ИО можно представить следующим образом:

1. Определяем некоторую начальную переменную («температуру» T=T_max и запускаем процесс обучения НС из некоторой начальной точки .

2. Пока Т>0, повторяем L раз следующие шаги:

• выбираем новое решение из окрестности ;

• рассчитываем изменение целевой функции ;

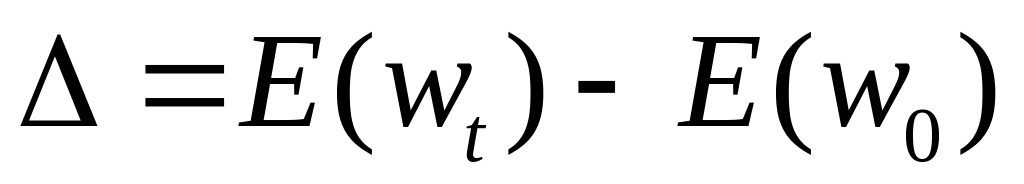• если 0, принимаем ;

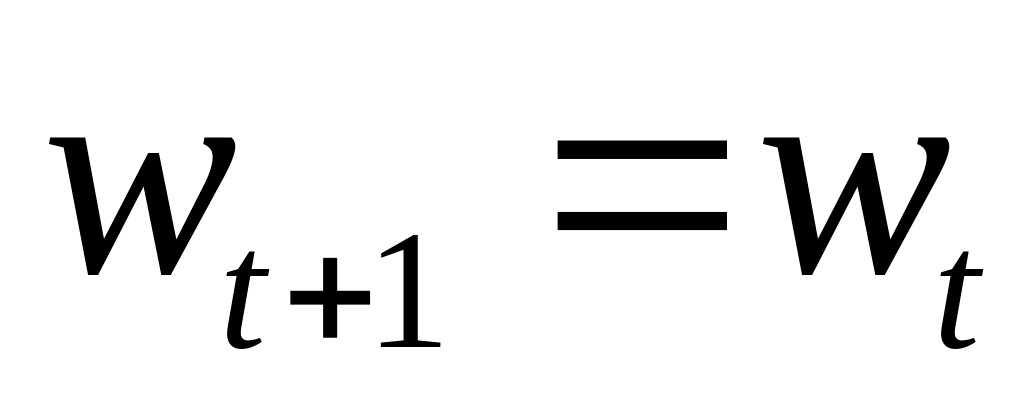• если >0, то вычисляем вероятность 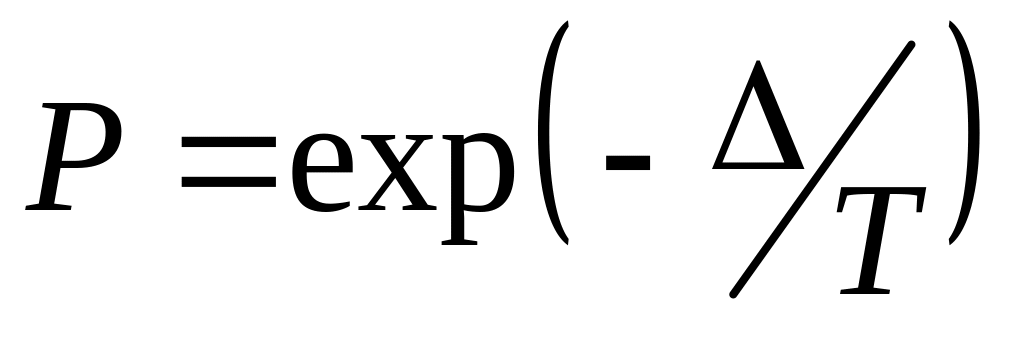, выбираем случайное число R(0,1) и, если RP, то , в противном случае (R>P) .

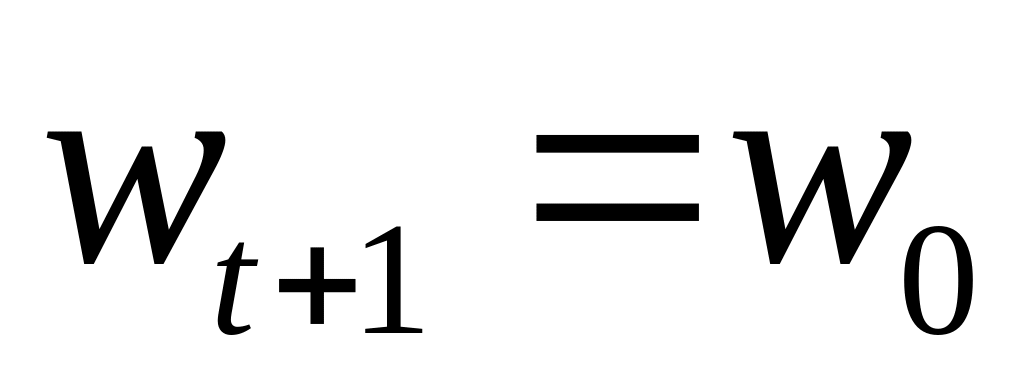3. Уменьшаем температуру (T_k=rT_k-1) с использованием коэффициента уменьшения r(0,1) и повторяем п. 2.

4. При снижении Т до нуля обучаем НС любым из представленных выше детерминированных методов.

Эффективность метода ИО сильно зависит от выбора T_max, L и r. Величина T_max определяется из предварительных имитационных экспериментов таким образом, чтобы обеспечить реализацию не менее 50% последующих случайных изменений решения. Выбор максимальных L и r для конкретных температурных уровней менее однозначен и должен учитывать динамику изменения в зависимости от количества выполненных циклов обучения. Общие рекомендации, вытекающие из компьютерных экспериментов, таковы: если время обучения ограничено, его лучше потратить на один процесс ИО с соответствующим удлинением циклов, если же моделирование может быть более длительным, статистически лучшие результаты достигаются при многократной реализации процесса ИО с большими (близкими к 1) значениями r и последующим выбором оптимального решения.

Таким образом, метод ИО наиболее эффективен для полимодальных комбинаторных проблем с большим числом возможных решений, например, для машины Больцмана, в которой каждое состояние системы (с различной вероятностью) считается допустимым. В общем же случае при решении наиболее распространенных задач обучения многослойных НС наилучшие результаты достигаются применением стохастических методов совместно с детерминированными алгоритмами локальной оптимизации.